Cours d'introduction à la statistique et à l'analyse de données : Notes de cours
Table des matières
- 1. Introduction
- 2. Prise en main de
Python - 3. Échantillon IID et estimation de densité
- 4. Estimation par maximisation de la vraisemblance
- 4.1. La fonction de vraisemblance
- 4.2. Estimateur du maximum de vraisemblance
- 4.3. Pourquoi l'EMV est-il un estimateur « sensé » ?
- 4.4. Théorie asymptotique de l'EMV
- 4.5. Une théorème dont le hypothèses sont plus faibles
- 4.6. Intervalles de confiance
- 4.7. Exemple : un compteur de photons à temps mort
- 4.7.1. Expression analytique et valeur numérique de l'EMV
- 4.7.2. Erreur type et intervalle de confiance à 95% avec la méthode de Wald
- 4.7.3. Graphe comparant la fonction de log vraisemblance avec son approximation quadratique
- 4.7.4. Intervalle de confiance à 95% avec la méthode du rapport de vraisemblance
- 4.7.5. Exercice
- 4.7.6. Solution
- 4.7.7. Remarques
- 5. Quelques exercices
(setq python-shell-interpreter "ipython2" python-shell-prompt-regexp "In \\[[0-9]+\\]: " python-shell-prompt-output-regexp "Out\\[[0-9]+\\]: " python-shell-completion-setup-code "from IPython.core.completerlib import module_completion" python-shell-completion-module-string-code "';'.join(module_completion('''%s'''))\n" python-shell-completion-string-code "';'.join(get_ipython().Completer.all_completions('''%s'''))\n") ;; Python and Babel (setq org-babel-python-command "ipython2 --no-banner --classic --no-confirm-exit") (defadvice org-babel-python-evaluate-session (around org-python-use-cpaste (session body &optional result-type result-params) activate) "add a %cpaste and '--' to the body, so that ipython does the right thing." (setq body (concat "%cpaste\n" body "\n--")) ad-do-it (setq ad-return-value (replace-regexp-in-string "\\(^Pasting code; enter '--' alone on the line to stop or use Ctrl-D\.[\r\n]:*\\)" "" ad-return-value))) (setq org-src-preserve-indentation t) (setq org-babel-python-command "ipython2") (setq org-export-babel-evaluate nil)
import shelve db = shelve.open("coursIntroStat2014.db",protocol=-1)
1 Introduction
Le cours va être orienté vers des applications « réelles » (ou assez proches de celles-ci). Je ne passerai pas de temps à prouver les théorèmes que nous allons employer, mais après (ou avant) les avoir énoncés, j'emploierai des simulations les illustrant. Les bouquins indiqués en fin d'introduction contiennent les preuves. Je précise aussi que j'emploie la locution « analyse de données » dans l'intitulé du cours au sens « naïf » du terme, c'est-à-dire pas comme les statisticiens français qui entendent par là un ensemble de méthodes d'analyse exploratoire impliquant principalement l'analyse en composantes principales (ACP). Ici « analyse de données » correspond à la situation familière à toute personne ayant passé ne serait-ce qu'une journée dans un laboratoire expérimentale : une expérience a été effectuée, les données sont « bruitées », on souhaite estimer certains paramètres — décrivant les données ou propres au modèle théorique supposé sous-jacent — ainsi que quantifier la précision de cette évaluation.
Comme faire de la statistique dans un contexte « réaliste » implique, de nos jours au moins, de manipuler de grands vecteurs ou table de données, nous ne pouvons pas vraiment nous passer d'utiliser un logiciel ; c'est pourquoi nous allons employer relativement « intensivement » dans ce cours le logiciel Python et ses extensions NumPy et SciPy pour le calcul scientifique. C'est un logiciel open source, gratuit et disponible sur tous les systèmes d'exploitation que vous êtes susceptibles de rencontrer. Nous allons employer l'interface IPython de python dans le cours (au moins pour les paties interactives).
Quelques bouquins de référence :
- « Statistique : la théorie et ses applications » de Michel Lejeune chez Springer, excellent ;
- Mathematical Statistics and Data Analysis de John Rice, aussi excellent mais en anglais ;
- All of Statistics et All of Nonparametric Statistics de Larry Wasserman, très bonnes synthèses mais un peu sèches pour les débutants ;
- Mathematical Statistics de Keith Knight, ma meilleure source pour les preuves des théorèmes ;
- Python. Essential Reference de David M. Beazley : un bouquin complet et assez succinct (donc aussi nécessairement « un peu » dense) dans l'énorme littérature
Python.
2 Prise en main de Python
Voir le chapitre 1 du bouquin de Beazley ainsi que le tutoriel officiel. Pour la partie « scientifique » de Python, les Python Scientific Lecture Notes constituent un excellent point de départ.
2.1 Utilisation de Python
2.1.1 Python « de base »
De nombreuses « interfaces utilisateurs » sont disponible pour Python. La plus simple est démarrée en ligne de commande avec :
python
Pour pouvoir faire des calculs avec numpy et générer des graphiques avec matplotlib, le plus simple est alors d'importer dans leur intégralité quelques modules :
>>> from numpy import * >>> from pylab import *
avant de passer en mode interactif avec :
>>> ion()
Ce qui permet de générer des graphes avec par exemple :
>>> plot([1,2,3,4,5],[5,2,7,0,1])
Pour éditer du code, vous devrez utiliser votre éditeur préféré (gEdit reconnaît le syntaxe Python, comme beaucoup d'autres éditeurs), puis copiez et coller dans votre console.
2.1.2 IDLE
IDLE est l'environnement de développement intégré inclut par défaut dans toute distribution complète de Python (celle de Ubuntu n'est pas complète de ce point de vue et il faut installer IDLE en plus). IDLE est démarré comme Python avec :
idle
De même qu'avec l'interface de base, il faudra charger les modules numpy et pylab. Un différence est que les graphiques interactifs ne sont pas possible, il faut taper des séquences de commandes comme :
>>> figure(1) >>> plot([1,2,3,4,5],[5,2,7,0,1]) >>> show()
et pendant que la fenêtre graphique est ouverte, il n'est pas possible d'entrer des commandes en console Python… Par contre, IDLE vient avec un éditeur assez performant de code Python.
2.1.3 IPython
Dans le cadre du cours, je vous recommande d'utiliser IPython, une console « hypertrophiée » pour faire du calcul scientifique interactif avec Python (qu'il faut installer en plus sur la plupart des distributions Linux). Comme les deux précédentes, on démarre avec :
ipython
Ensuite, la « commande magique » (la notion de commande magique fait partie du jargon, un peu prétentieux à mon sens, de IPython) :
%pylab
donne accès à numpy, matplotlib, etc.
Pour éditer du code, vous devrez utiliser votre éditeur préféré (gEdit reconnaît le syntaxe Python, comme beaucoup d'autres éditeurs), puis copiez et coller dans votre console avec la « commande magique » %paste.
2.1.4 emacs
L'éditeur emacs vient avec de nombreux modes Python. Personnellement, j'utilise le mode par défaut. Pour utiliser IPython à partir de emacs, il suffit d'affecter "ipython" à la variable python-shell-interpreter avec :
(setq python-shell-interpreter "ipython")
Pour avoir des choses un peu plus sophistiquées on pourra taper :
(setq python-shell-interpreter "ipython2" python-shell-prompt-regexp "In \\[[0-9]+\\]: " python-shell-prompt-output-regexp "Out\\[[0-9]+\\]: " python-shell-completion-setup-code "from IPython.core.completerlib import module_completion" python-shell-completion-module-string-code "';'.join(module_completion('''%s'''))\n" python-shell-completion-string-code "';'.join(get_ipython().Completer.all_completions('''%s'''))\n")
2.1.5 Le reste
Ce qui précède est bien sûr loin d'être exhaustif, pour plus de choix, consultez le wiki Python. Si vous cherchez des interfaces sophistiquées type environnement de développement intégré (Integrated Development Environment IDE), jetez un œil sur pycharm — dont la version « de base » est gratuite — et sur spyder.
3 Échantillon IID et estimation de densité
Nous allons commencer la « vraie statistique » avec l'étude d'échantillons identiquement et indépendemment distribués (IID) de taille n variable et suivant une loi dont nous noterons la fonction de répartition F :
\[X_1,\ldots,X_n \stackrel{\mathrm{IID}}{\sim} \mathrm{F} \, .\]
Nous suivons ici la convention des statisticiens et des probabilistes qui emploient des majuscules pour les variables aléatoires (qui ne sont pas directement observables) et de minuscules pour leurs réalisations (qui sont observables).
Lorsque nous disposons d'un tel échantillon qui va être typiquement assez grand (plus d'une cinquantaine d'observations), la lecture d'une table des valeurs n'est pas forcément très informative et en plus du résumé à cinq nombres — que nous avons vu dans nos cours d'« illustration » sur le tri des potentiels d'action — nous souhaitons avec une représentation graphique. Une première façon de faire un « graphe des données » passe par la fonction de répartition empirique \(\widehat{\mathrm{F}}\) définie par :
3.1 Fonction de répartition empirique
Soient \(X_1,\ldots,X_n \stackrel{\mathrm{IID}}{\sim} \mathrm{F}\), \(\widehat{\mathrm{F}}\) est une fonction limitée à gauche, continue à droite (cadlag) qui met un poids \(1/n\) sur chaque point \(X_i\) :
\[\widehat{\mathrm{F}} = \frac{1}{n} \sum_{i=1}^n \mathrm{I}(X_i \le x) \, ,\]
où
\[\mathrm{I}(X_i \le x) = \left\{ \begin{array}{lr} 1 & \mathrm{si}\quad X_i \le x\\ 0 & \mathrm{si}\quad X_i > x.\end{array} \right. \]
De façon peut-être plus parlante, la fonction de répartition empirique (FRE) est une fonction qui saute de \(1/n\) à chaque observation \(X_i\). Si nous notons \(X_{(i)}\) la version ordonnée de l'échantillon \(\{X_1,\ldots,X_n\}\), c.-à-d. que :
- \(X_{(1)} = \min \{X_1,\ldots,X_n\}\) ;
- \(X_{(2)} = \min \{X_1,\ldots,X_n\} \setminus \{X_{(1)}\}\) ;
- \(X_{(k)} = \min \{X_1,\ldots,X_n\} \setminus \{X_{(1)},\ldots,X_{(k-1)}\}\) ;
- \(X_{(n)} = \max \{X_1,\ldots,X_n\}\) 1 ;
alors le graphe de la FRE est une fonction constante par morceaux, continue à droite et limitée à gauche (sa valeur en un point de saut est la hauteur de la marche du coté droit du saut).
3.2 Exemple et mise en œuvre en Python
Nous commençons par télécharger un jeu de données depuis le site du livre All of Nonparametric Statistics de Larry Wasserman. Plus particulièrement, nous récupérons le jeu Nerve Data avec :
wget http://www.stat.cmu.edu/~larry/all-of-nonpar/=data/nerve.dat
Les données contiennent les intervals de temps entre deux potentiels post-synaptiques miniatures enregistrés à la jonction neuro-musculaire (la description du jeu de données fournie pas Wasserman est inexacte). Il y 799 intervals (mesurés en seconde) avec 6 intervals par ligne (séparés par plusieurs espaces : des tabs) pour les 133 premières lignes et 1 interval sur la 134ième.
On charge les données dans Python avec :
ppsm = [] for line in open("nerve.dat"): elt = line.split('\t') if elt[1] != '': ppsm += [float(x) for x in line.split('\t')] else: ppsm += [float(elt[0])]
db['ppsm'] = ppsm
Pour pouvoir profiter pleinement des aspects interactifs de IPython nous utilisons la « commande magique » %pylab :
%pylab
Une façon un peu « rustique » d'obtenir le résumé à cinq nombres est d'employer la fonction percentile de la librarie numpy :
[round(percentile(ppsm,q),2) for q in linspace(0,100,5)]
[0.01, 0.07, 0.15, 0.3, 1.38]
Nous définissons maintenant une fonction qui génère un graphe de \(\widehat{\mathrm{F}}\) qui est une fonction continue par morceaux at dont tous les morceaux sont horizontaux. La position des sauts ou discontinuité correspond aux valeurs observées de notre échantillon, l'ampliude des sauts est toujours la même :
def plot_fre(x, domain = None, color='black', lw=1): X = sort(x) n = len(x) Y = arange(1,n+1)/float(n) if domain is None: domain = [floor(X[0]),ceil(X[n-1])] for i in range(n-1): plot(X[i:(i+2)],[Y[i],Y[i]],color=color,lw=lw) xlim(domain) ylim([0,1]) hlines(0,domain[0],X[0],colors=color,lw=lw) hlines(1,X[n-1],domain[1],colors=color,lw=lw)
Nous testons sur nos données :
plot_fre(ppsm) ## Python 2 ! xlabel(u"Temps entre événements (s)") ylabel(u"Fréquence")
Text(50.4688,0.5,u'Fr\xe9quence')
Le préfixe « u » utilisé pour la génération des labels est spécifique à Python 2 et précise que la chaîne de caractères préfixées est un « littéral UTF8 », avec Python 3, ce n'est plus nécessaire et on utiliserait :
plot_fre(ppsm) ## Python 3 ! xlabel("Temps entre événements (s)") ylabel("Fréquence")
savefig('img/coursIntroStats2014/fct-repartition-empirique-nerve.png') close() 'img/coursIntroStats2014/fct-repartition-empirique-nerve.png'
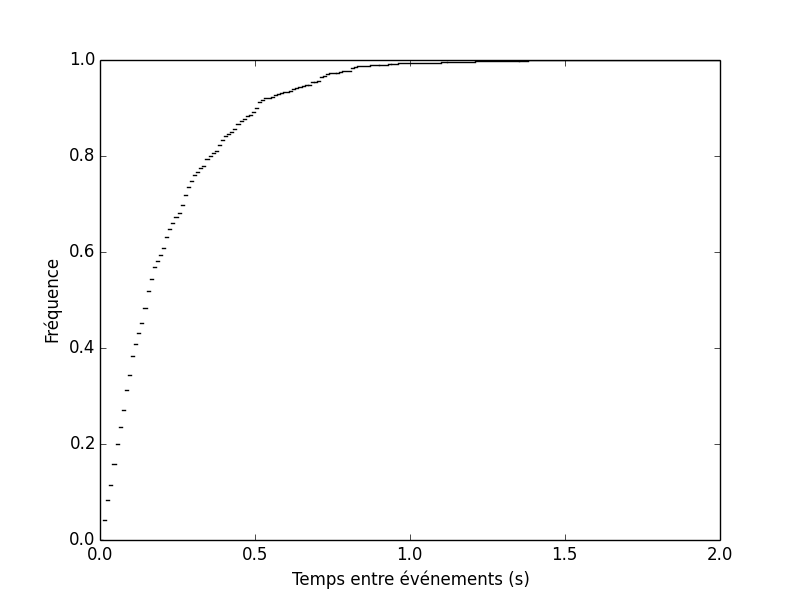
Figure 1 : Fonction de répartition empirique du jeu de données nerve.dat disponible sur le site http://www.stat.cmu.edu/~larry/all-of-nonpar/data.html associé au libre All of Nonparametric Statisitcs de Larry Wasserman.
Il est possible (et même simple) de construire une bande de confiance autour de \(\widehat{\mathrm{F}}\), c.-à-d., un domaine à l'intérieur duquel la vraie fonction de répartition \(\mathrm{F}\) a une probabilité donnée de se trouver dans son intégralité (p 14-15, du bouquin de Wasserman). Nous y reviendrons (exercice), mais la construction d'un tel domaine repose sur l'inégalité de Dvoretzky-Kiefer-Wolfowitz (DKW) : \[\mathrm{Pr}\left(\sup_x \mid \mathrm{F}(x) - \widehat{\mathrm{F}}_{n}(x) \mid > \epsilon \right) \le 2\, e^{-2 n \epsilon^2} \, ;\] où nous avons fait apparaître explicitement la taille \(n\) de l'échantillon.
Solution de l'exercice : Supposons qu'on souhaite : \(\mathrm{Pr}\left(\sup_x \mid \mathrm{F}(x) - \widehat{\mathrm{F}}_{n}(x) \mid > \epsilon \right) \le 1-\alpha\) ; pour fixer les idées nous pourrons prendre \(\alpha = 0.95\) ou \(\alpha = 0.99\) (c.-à-d. qu'on veut avoir une probabilité de moins de 5 % ou de moins de 1 % pour que la vraie fonction de répartition soit en un point au moins hors de la bande). On résout pour \(\epsilon\) et on trouve immédiatement : \[\epsilon(\alpha) = \sqrt{\frac{1}{2 n}} \sqrt{\log\left(\frac{2}{1-\alpha}\right)} \, .\]
Le code Python d'une fonction qui rajoute les bornes de la bande de confiance suit :
def plot_fre_band(x, alpha = 0.95, domain = None, color='black', lw=1): X = sort(x) n = len(x) Y = arange(1.,n+1)/n epsilon = sqrt(log(2/(1-alpha))/2/n) U = clip(Y+epsilon,0,1) L = clip(Y-epsilon,0,1) if domain is None: domain = [floor(X[0]),ceil(X[n-1])] for i in range(n-1): plot(X[i:(i+2)],[U[i],U[i]],color=color,lw=lw) plot(X[i:(i+2)],[L[i],L[i]],color=color,lw=lw) xlim(domain) ylim([0,1]) hlines(0,domain[0],X[0],colors=color,lw=lw) hlines(1,X[n-1],domain[1],colors=color,lw=lw)
3.3 Estimation non-paramétrique de densité
Nous supposons à présent que \(f = \mathrm{F}'\) existe. Le but de l'estimation non-paramétrique de densité est d'obtenir un estimateur de \(f\) en faisant aussi peu d'hypothèses que possible sur \(f\). Nous allons noter \(\widehat{f_n}\) notre estimateur. D'une façon générale, les estimateurs que nous allons considérer vont dépendre d'un paramètre de lissage \(h\) et c'est le choix \(h\) qui va nous occuper.
3.3.1 Exemple : densité de « Bart Simpson »
Nous allons considérer la densité suivante : \[f(x) = \frac{1}{2}\, \phi(x;0,1) + \frac{1}{10} \, \sum_{j=0}^4 \phi\left(x;(j/2)-1,1/10\right) \, ,\] où \(\phi(x; \mu, \sigma)\) désigne la densité d'une loi normale de moyenne \(\mu\) et d'écart type \(\sigma\).
import scipy from scipy.stats import norm def bart_simpson_pdf(x): res = 0.5*norm.pdf(x) for j in range(5): res += norm.pdf(x,loc=j*0.5-1,scale=0.1)*0.1 return res
def bart_simpson_rvs(size=1): weights = array([0.5,0.1,0.1,0.1,0.1,0.1]) means = array([0,-1,-0.5,0,0.5,1]) sigmas = array([1,0.1,0.1,0.1,0.1,0.1]) res = norm.rvs(size=size) k = list(numpy.random.choice(arange(6),size=size,p=weights)) locs = means[k] scales = sigmas[k] res *= scales res += locs return res
seed(20110928)
bart_simpson_test0 = bart_simpson_rvs(1000)
def bart_simpson_cdf(x): res = 0.5*norm.cdf(x) for j in range(5): res += norm.cdf(x,loc=j*0.5-1,scale=0.1)*0.1 return res
def fait_fre(echantillon): y = sort(echantillon) n = float(len(echantillon)) def fre(x): return sum(y <= x)/n return fre
bart_simpson_test0_fre = fait_fre(bart_simpson_test0) bb = arange(-3,3.0001,0.0001) bart_simpson_test0_delta = array([bart_simpson_test0_fre(bb[i+1])-bart_simpson_test0_fre(bb[i]) for i in range(len(bb)-1)]) bb_mid = bb[:-1] + diff(bb)/2. kernelBest = norm.pdf(arange(-0.25,0.2501,0.0001),scale=0.05) from scipy.signal import fftconvolve bart_simpson_test0_pdf_best = fftconvolve(bart_simpson_test0_delta,kernelBest,mode='same') kernelBest_over_10 = norm.pdf(arange(-0.025,0.02501,0.0001),scale=0.005) bart_simpson_test0_pdf_best_over_10 = fftconvolve(bart_simpson_test0_delta,kernelBest_over_10,mode='same') kernelBest_times_10 = norm.pdf(arange(-2.5,2.501,0.0001),scale=0.5) bart_simpson_test0_pdf_best_times_10 = fftconvolve(bart_simpson_test0_delta,kernelBest_times_10,mode='same')
La figure suivante montre la densité de Bart Simpson ainsi que trois estimations de celle-ci basée sur un estimateur à noyau construit à partir du même échantillon de taille 1000 en utilisant trois valeurs du paramètre de lissage:
subplot(221) xx = linspace(-3.,3,501) plot(xx,bart_simpson_pdf(xx),color='black') title(u'Vraie densité') xlim([-3,3]) ylim([0,1]) subplot(222) plot(bb_mid,bart_simpson_test0_pdf_best_over_10,color='black') title(u'Pas assez lissée') xlim([-3,3]) ylim([0,1]) subplot(223) plot(bb_mid,bart_simpson_test0_pdf_best,color='black') title(u"C'est bon !") xlim([-3,3]) ylim([0,1]) subplot(224) plot(bb_mid,bart_simpson_test0_pdf_best_times_10,color='black') title(u'Trop lissée') xlim([-3,3]) ylim([0,1]) savefig('img/coursIntroStats2014/Clone-Fig6p1-AONPS.png') close() 'img/coursIntroStats2014/Clone-Fig6p1-AONPS.png'
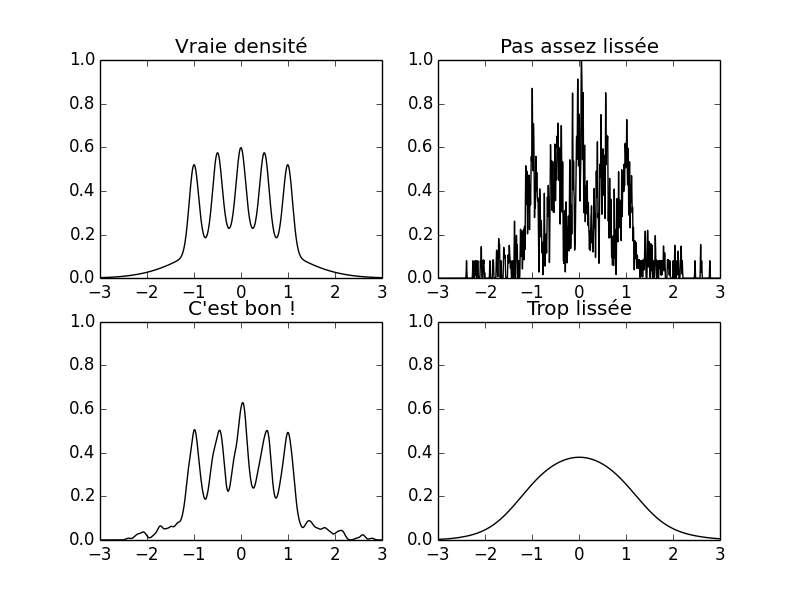
Figure 2 : En haut à gauche : la densité de « Bart Simpson ». En bas à gauche : estimateur à noyau avec paramètre de lissage « idéal » (\(h=0.05\)). En haut à droite : estimateur à noyau avec paramètre de lissage « trop petit » (\(h=0.5\)). En bas à droite : estimateur à noyau avec paramètre de lissage « trop grand » (\(h=0.5\)). Les trois estimateurs à noyau ont été calculés à partir du même échantillon de taille 1000.
3.3.1.1 Exercice
Vous coderez en Python (ou en R pour ceux qui préfèrent) :
- la densité de Bart Simpson (vous utiliserez la fonction norm.pdf) ;
- un générateur de variables aléatoires de loi Bart Simpson (vous utiliserez la fonction norm.rvs).
Vous générerez ensuite un échantillon de taille 1000 suivant cette loi. Puis :
- vous construirez le graphe de sa fonction de répartition empirique ;
- vous y ajouterez le graphe de la fonction de répartition de Bart Simpson (vous utiliserez la fonction norm.cdf).
Solution : Le code suivant définit la fonction de densité :
<<definition-bart_simpson_pdf>>
Le code suivant définit le générateur. L'idée est de tirer la composante (la densité est un mélange de six composantes gaussiennes) avec les bons poids, puis de tirer suivant la composante sélectionnée :
<<definition-bart_simpson_rvs>>
Lorsque nous générons l'échantillon, nous n'oublions pas de spécifier la graine du générateur :
<<generation-echantillon-bart_simpson>>
Nous construisons le graphe de la FRE (en rajoutant une bande de confiance avec \(\alpha = 0.95\)) :
plot_fre(bart_simpson_test0)
plot_fre_band(bart_simpson_test0,color='blue')
Nous définissons la fonction de répartition de la loi de Bart-Simpson :
<<definition-bart_simpson_cdf>>
Nous rajoutons la fonction de répartition théorique au graphe :
xx = linspace(-3,3,501) plot(xx,bart_simpson_cdf(xx),color='red')
savefig('img/coursIntroStats2014/Exercice-Bart-Simpson-1.png') close() 'img/coursIntroStats2014/Exercice-Bart-Simpson-1.png'
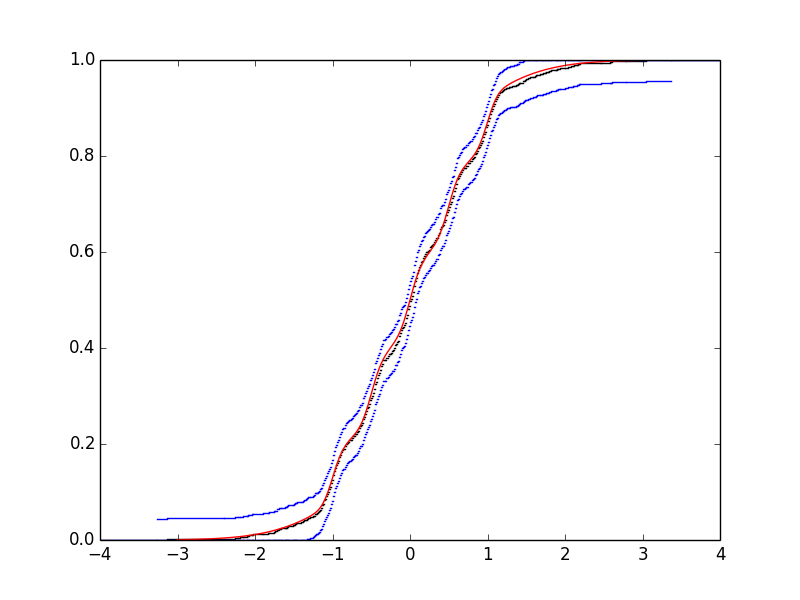
Figure 3 : FRE de l'échantillon généré suivant la loi de Bart-Simpson (noir) avec bande de confiance à 95 % (bleu) et fonction théorique (rouge).
3.3.2 Validation croisée
Nous allons juger la qualité d'un estimateur \(\widehat{f_n}\) par son erreur quadratique intégréee moyenne, \(R = \mathrm{E}(L)\) où :
\[L = \int \left(\widehat{f_n}(x) - f(x)\right)^2 dx\]
est l'erreur quadratique intégrée. Ici l'espérance est prise par rapport à la loi d'un vecteur de \(n\) variables aléatoires IID de loi \(\mathrm{F}\) ; nous notons \(\widehat{f_n}(x)\) ce que nous pourrions écrire plus explicitement : \(\widehat{f_n}(x;X_1,\ldots,X_n)\). Ainsi avec des notations plus lourdes nous pouvons écrire :
\[R = \int_{X_1} \ldots \int_{X_n} \left(\int \left(\widehat{f_n}(x;X_1,\ldots,X_n) - f(x)\right)^2 dx\right) dF(X_1) \cdots dF(X_n) \; .\]
La méthode habituelle pour estimer l'erreur quadratique intégrée moyenne est la validation croisée ou, plus précisemment, ce qu'on désigne en anglais par leave-one-out-cross-validation. Avant de la définir, nous allons un peu « travailler » notre expression de l'erreur quadratique intégrée : \[\begin{array}{l,l,l}L(h) & = & \int \left(\widehat{f_n}(x) - f(x)\right)^2 dx \, , \\ & = & \int \widehat{f_n}^2(x)\, dx - 2\, \int \widehat{f_n}(x) \, f(x) dx + \int f^2(x) dx \, .\end{array}\] Comme le dernier terme ne dépend pas de \(h\), minimiser l'erreur quadratique intégrée moyenne revient à minimiser l'espérance de : \[J(h) = \int \widehat{f_n}^2(x)\, dx - 2\, \int \widehat{f_n}(x) \, f(x) dx \, .\] Pour faire cours, nous allons appeler \(J(h)\) l'erreur quadratique intégrée moyenne, même si cette quantité diffère de la vraie erreur quadratique intégrée moyenne par le terme constant \(\int f^2(x) dx\).
Notre estimateur de l'erreur quadratique intégrée moyenne par validation croisée est alors définit par : \[\widehat{J}(h) = \int \widehat{f_n}^2(x)\, dx - \frac{2}{n} \sum_{i=1}^n \widehat{f}_{(-i)}(X_i) \] où \(\widehat{f}_{(-i)}\) est l'estimateur de densité obtenu après avoir retiré la \(i\) -ième observation de l'échantillon. Nous appellerons \(\widehat{J}(h)\) le « score de validation croisée » ou « l'erreur quadratique intégrée moyenne estimée ».
3.3.3 Les histogrammes
L'estimateur de densité le plus simple et, sans aucun doute, le plus communément employé est l'histogramme. Supposons que \(f\) admet pour support un intervalle que nous pourrons prendre (moyennant une transformation linéaire si nécessaire) comme étant \([0,1]\). Soit \(m\) un entier, nous définissons les classes (bins en anglais) : \[C_1 = \left[0,\frac{1}{m}\right), \quad C_2 = \left[\frac{1}{m},\frac{2}{m}\right), \quad \ldots, \quad C_m = \left[\frac{m-1}{m},1\right) \, .\] Nous définissons :
- la largeur de classe (binwidth) \(h = 1/m\) ;
- \(Y_j\) la variable aléatoire décrivant le nombre d'observations dans la classe \(C_j\) ;
- \(\hat{p}_j = Y_j/n\) ;
- \(p_j = \int_{C_j} \, f(u) \, du\).
L'(estimateur) histogramme est alors définit par : \[\widehat{f_n}(x) = \sum_{j=1}^m \frac{\hat{p}_j}{h}\, I(x \in C_j) \, .\]
Pour comprendre l'origine de cet estimateur, il suffit de remarquer que : \[\mathrm{E}\left(\widehat{f_n}(x)\right) = \frac{\mathrm{E}(\hat{p}_j)}{h} = \frac{p_j}{h} = \frac{\int_{C_j} \, f(u) \, du}{h} \approx \frac{f(x)\, h}{h} = f(x) \, .\]
On en déduit alors :
Théorème Soient \(x\) et \(m\) fixés et soit \(C_j\) la classe contenant \(x\) ; alors \[\mathrm{E}\left(\widehat{f_n}(x)\right) = \frac{p_j}{h} \quad \mathrm{et} \quad \mathrm{Var}\left(\widehat{f_n}(x)\right) = \frac{p_j\, (1-p_j)}{n\, h^2} \, .\]
Le théorème suivant montre qu'il est inutile de (re)calculer \(n\) estimateurs pour obtenir la valeur de l'erreur quadratique intégrée moyenne estimée.
Théorème Nous avons l'identité suivante : \[\widehat{J}(h) = \frac{2}{h\, (n-1)} - \frac{n+1}{h\, (n-1)} \sum_{j=1}^m \hat{p}_j^2 \, .\]
Preuve (Avant de lire les lignes suivantes essayer d'obtenir la preuve vous même.) Par définition : \[\widehat{J}(h) = \int \widehat{f_n}^2(x)\, dx - \frac{2}{n} \sum_{i=1}^n \widehat{f}_{(-i)}(X_i) \, , \] \[\widehat{f_n}(x) = \sum_{j=1}^m \frac{\hat{p}_j}{h}\, I(x \in C_j) \, ,\] \[\hat{p}_j = Y_j/n \, .\] Le premier terme de \(\widehat{J}(h)\) devient donc : \[\begin{array}{l,l,l} \int \widehat{f_n}^2(x)\, dx & = & \int \left(\sum_{j=1}^m \frac{\hat{p}_j}{h}\, I(x \in C_j)\right) \, \left(\sum_{k=1}^m \frac{\hat{p}_k}{h}\, I(x \in C_k)\right) \, dx \\ & = & \sum_{j=1}^m \sum_{k=1}^m \frac{\hat{p}_j}{h} \frac{\hat{p}_k}{h} \int I(x \in C_j) \, I(x \in C_k) \, dx \\ & = & \sum_{j=1}^m \frac{\hat{p}^2_j}{h} \end{array}\] où on a utlisé le fait : \[I(x \in C_j) \, I(x \in C_k) = \left\{ \begin{array}{l l} I(x \in C_j) \quad \mathrm{si} \quad j=k \, ,\\ 0 \quad \mathrm{sinon} \end{array}\right.\] et : \[\int I(x \in C_j)\, dx = \int_{\frac{j-1}{m}}^{\frac{j}{m}} dx = \frac{1}{m} = h \, .\]
Pour calculer le second terme, \(\sum_{i=1}^n \widehat{f}_{(-i)}(X_i)\), nous commençons par trouver l'expression de \(\widehat{f}_{(-i)}(x)\) : \[\begin{array}{l,l,l} \widehat{f}_{(-i)}(x) & = & \sum_{j=1}^m \frac{\hat{p}_{(-i),j}}{h}\, I(x \in C_j) \\ & = & \sum_{j=1}^m \frac{Y_{(-i),j}}{h \, (n-1)}\, I(x \in C_j) \\ & = & \sum_{j=1,j \neq k}^m \frac{Y_{(-i),j}}{h \, (n-1)}\, I(x \in C_j) + \frac{Y_{(-i),k}}{h \, (n-1)}\, I(x \in C_k) \end{array}\]
où \(k\) est l'indice de la classe contenant \(X_i\). Mais : \[Y_{(-i),j} = \left\{ \begin{array}{l l} Y_j \quad \mathrm{si} \quad j \neq k \\ Y_j - 1 \quad \mathrm{si} \quad j = k\end{array} \right.\] d'où : \[\begin{array}{l,l,l} \widehat{f}_{(-i)}(x) & = & \frac{n}{n-1} \sum_{j=1}^m \frac{Y_j}{h \, n}\, I(x \in C_j) - \frac{1}{h\, (n-1)} I(x \in C_k) \\ & = & \frac{n}{n-1} \sum_{j=1}^m \frac{\hat{p}_j}{h}\, I(x \in C_j) - \frac{1}{h\, (n-1)} I(x \in C_k) \end{array}\]
On en déduit que : \[\widehat{f}_{(-i)}(X_i) = \frac{n}{n-1} \frac{\hat{p}_k}{h} - \frac{1}{h\, (n-1)}\] et que : \[\begin{array}{l,l,l} \sum_{i=1}^n \widehat{f}_{(-i)}(X_i) & = & \frac{n}{n-1} \sum_{k=1}^m\frac{Y_k \, \hat{p}_k}{h} - \frac{n}{h\, (n-1)} \\ & = & \frac{n^2}{n-1} \sum_{k=1}^m\frac{\hat{p}^2_k}{h} - \frac{n}{h\, (n-1)} \end{array}\] où le fait que \(Y_k\) des \(X_i\) se trouvent dans la classe \(k\) a été utilisé. En sommant les deux termes en en réarrangeant il vient : \[\widehat{J}(h) = \frac{2}{h\, (n-1)} - \frac{n+1}{h\, (n-1)} \sum_{j=1}^m \hat{p}_j^2 \, .\]
Question Pourquoi retire-t-on l'observation de \(X_i\) dans notre définition de l'erreur quadratique intégrée moyenne estimée ?
Réponse Pour le comprendre, vous pourrez considérer l'estimateur : \[\check{J}(h) = \int \widehat{f_n}^2(x)\, dx - \frac{2}{n} \sum_{i=1}^n \widehat{f}_{n}(X_i) \, .\] Avec des \(X_i\) tous différents, il est possible de trouver un \(h < \min \left(X_{(i+1)}-X_{(i)}\right)\), c'est-à-dire que pour \(h\) assez petit, les classes de notre histogrammes contiennent soit 0 soit 1 observation (\(Y_i = 0\) ou \(Y_i = 1\) pour tout \(i\)). On montre alors facilement que pour tout \(h\) assez petit : \[\check{J}(h) = - \frac{1}{h \, n} \, .\] C'est-à-dire que le \(h\) optimal est nul et l'histogramme devient un peigne de Dirac : \[\check{f}_n(x) = \frac{1}{n} \sum_{i=1}^n \delta_{X_i}(x) \, .\] En conséquence, si \(X_{extra}\) est une nouvelle observation de \(F\) nous aurons : \(\check{f}_n(X_{extra}) = 0\)…
3.3.3.1 Exercice : mise en œuvre en Python de l'estimateur de l'erreur quadratique intégrée moyenne par validation croisée
- vous écrirez une fonction
Pythonqui retourne \(\widehat{J}(h)\) ; - vous l'utiliserez pour minimiser cette même quantité en employant l'échantillon simulé suivant la loi de Bart Simpson ;
- vous comparerez dans ce même cas, \(\widehat{J}(h)\) et \(J(h)\) ;
- vous pourrez répéter ces opérations avec un échantillon de taille 10 fois plus petite et un autre de taille 10 fois plus grande ;
- vous répéterez le point 2 avec le jeu de données Sloan Digital Sky Survey du site de L. Wasserman.
Réponses
Définition de la fonction retournant \(\widehat{J}(h)\). Pour calculer cette quantité, nous avons besoin de calculer les \(\hat{p}_j\), c'est-à-dire, le nombre d'observation par classe divisé par le nombre total d'observation. Nous commençons par définir une fonction « utilitaire » qui nous renvoie la FRE d'un échantillon :
<<definition-fait_fre>>
Cette fonction renvoie une fonction et la fonction renvoyée est un peu particulière : c'est une fermeture ou clôture (closure en anglais). C'est une fonction qui a « capturé » les variables locales de son environnement lexical. Quand nous appelons :
bart_simpson_test0_fre = fait_fre(bart_simpson_test0)
Une version ordonnée de bart_simpson_test0 est présente dans l'environnement propre (la fermeture) de bart_simpson_test0_fre, c'est ce qui lui permet d'effectuer sa tâche :
bart_simpson_test0_fre(0.15)
0.57899999999999996
Nos pouvons à présent utiliser notre FRE pour construire l'histogramme (les \(\hat{p}_j\)) qui sont donnés par la différence de la FRE entre deux limites de classes successives :
def j_chapeau(echantillon,m): fre = fait_fre(echantillon) n = float(len(echantillon)) x_min = min(echantillon) x_max = max(echantillon) limites_classes = linspace(x_min,x_max,m+1) p_chapeau = array([fre(limites_classes[i]) for i in range(m+1)]) p_chapeau = diff(p_chapeau) return (2 - (n+1)*sum(p_chapeau**2))*m/(n-1)
Ici nous définissons notre fonction comme dépendant du nombre de classes \(m\) et pas de leur largeur (\(h=1/m\)).
Minimisation de \(\widehat{J}(h)\) sur les données simulées. Si nous l'appliquons à nos données simulées suivant la loi de Bart-Simpson nous obtenons :
mm = arange(1,501) j_bart_simpson_test0 = array([j_chapeau(bart_simpson_test0,i) for i in mm]) mm[argmin(j_bart_simpson_test0)]
77
db['j_bart_simpson_test0'] = j_bart_simpson_test0
Nous devrions donc choisir un histogramme construit avec 77 classes.
Comparaison de \(\widehat{J}(h)\) et \(J(h)\) sur les données simulées. Si nous remontons à la définition, nous voyons que : \[J(h) = \int \widehat{f_n}^2(x)\, dx - 2\, \int \widehat{f_n}(x) \, f(x) dx \, .\] Le début de notre preuve de « l'expression simplifiée » de \(\widehat{J}(h)\) nous donne pour le premier terme du second membre : \[\int \widehat{f_n}^2(x)\, dx = m \, \sum_{j=1}^m \hat{p}^2_j \, ,\] où plutôt que de diviser par \(h\) comme précédemment, je multiplie par \(m = 1/h\). Le second terme est : \[- 2\, \int \widehat{f_n}(x) \, f(x) dx = -2\, m \, \hat{p}_j \sum_{j=1}^m \int I(x \in C_j) \, f(x) \, dx \, ,\] où chacun des \(m\) morceaux de l'intégrale est directement obtenu à partir de la fonction de répartition \(F\) : \[- 2\, \int \widehat{f_n}(x) \, f(x) dx = -2\, m \, \sum_{j=1}^m \hat{p}_j \, \left(F(j/m) - F((j-1)/m)\right) \, .\]
Nous définissons donc une nouvelle fonction :
def j_vraie(echantillon,m): fre = fait_fre(echantillon) n = float(len(echantillon)) x_min = min(echantillon) x_max = max(echantillon) limites_classes = linspace(x_min,x_max,m+1) p_chapeau = array([fre(limites_classes[i]) for i in range(m+1)]) p_chapeau = diff(p_chapeau) f_sommee = diff(array([bart_simpson_cdf(limites_classes[i]) for i in range(m+1)])) return m*(sum(p_chapeau*(p_chapeau - 2*f_sommee)))
Nous l'appliquons :
j_vraie_bart_simpson_test0 = [j_vraie(bart_simpson_test0,i) for i in mm]
db['j_vraie_bart_simpson_test0'] = j_vraie_bart_simpson_test0
Et le nombre optimal de classes est :
mm[argmin(j_vraie_bart_simpson_test0)]
81
Ce qui n'est pas mal comparé aux 77 classes obtenues avec erreur quadratique intégrée moyenne estimée. Le graphe des deux erreurs quadratiques intégrées moyennes est obtenu avec :
plot(mm,j_bart_simpson_test0) plot(mm,j_vraie_bart_simpson_test0) xlabel('Nombre de classes') ylabel(u'Erreur quadratique intégrée moyenne')
Text(39.7188,0.5,u'Erreur quadratique int\xe9gr\xe9e moyenne')
savefig('img/coursIntroStats2014/Exercice-Bart-Simpson-2.png') close() 'img/coursIntroStats2014/Exercice-Bart-Simpson-2.png'
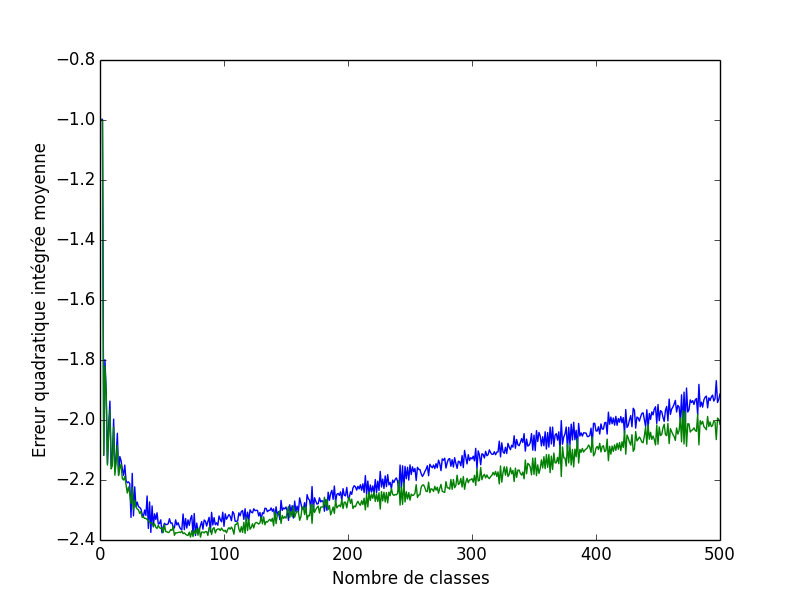
Figure 4 : En bleu, l'erreur quadratique intégrée moyenne estimée ; en vert, la vraie erreur quadratique intégrée moyenne.
À ce stade, nous pouvons aussi définir des fonctions construisant des histogrammes et les utiliser avec notre nombre de classes optimal :
def histogramme(echantillon,m): fre = fait_fre(echantillon) n = float(len(echantillon)) x_min = min(echantillon) x_max = max(echantillon) limites_classes = linspace(x_min,x_max,m+1) p_chapeau = array([fre(limites_classes[i]) for i in range(m+1)]) f_chapeau = diff(p_chapeau)/diff(limites_classes) return (limites_classes, f_chapeau) def histogramme_fct(echantillon,m): fre = fait_fre(echantillon) x_min = min(echantillon) x_max = max(echantillon) limites_classes = linspace(x_min,x_max,m+1) p_chapeau = array([fre(limites_classes[i]) for i in range(m+1)]) f_chapeau = diff(p_chapeau)/diff(limites_classes) def histo(x): if x < x_min or x > x_max: return 0 else: return f_chapeau[max(where(x >= limites_classes)[0])] return histo
histogram_fct
cb,f_chapeau = histogramme(bart_simpson_test0,77) plot(cb[1:],f_chapeau,ls='steps') ylabel(u'Densité estimée')
Text(50.4688,0.5,u'Densit\xe9 estim\xe9e')
savefig('img/coursIntroStats2014/Exercice-Bart-Simpson-3.png') close() 'img/coursIntroStats2014/Exercice-Bart-Simpson-3.png'
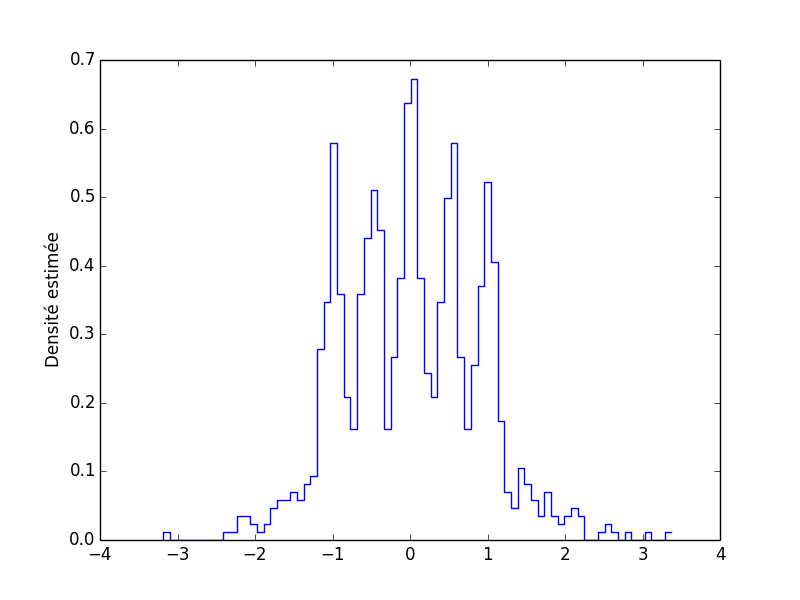
Figure 5 : Densité de Bart-Simpson estimée à partir d'un échantillon de taille 1000 avec un histogramme construit avec 77 classes (nombre optimal d'après l'erreur quadratique intégrée moyenne estimée).
La même chose avec un échantillon de taille 10 fois plus petite. On reprend ce que nous venons de faire :
j_bart_simpson_test0_div_10 = array([j_chapeau(bart_simpson_test0[:100],i) for i in mm]) mm[argmin(j_bart_simpson_test0_div_10)]
10
db['j_bart_simpson_test0_div_10'] = j_bart_simpson_test0_div_10
j_vraie_bart_simpson_test0_div_10 = [j_vraie(bart_simpson_test0[:100],i) for i in mm] mm[argmin(j_vraie_bart_simpson_test0_div_10)]
18
db['j_vraie_bart_simpson_test0_div_10'] = j_vraie_bart_simpson_test0_div_10
On peut comparer les courbes avec :
plot(mm,j_bart_simpson_test0_div_10) plot(mm,j_vraie_bart_simpson_test0_div_10)
La même chose avec un échantillon de taille 10 fois plus grande.
seed(20061001) bart_simpson_test1 = bart_simpson_rvs(10000) j_bart_simpson_test1 = array([j_chapeau(bart_simpson_test1,i) for i in mm]) mm[argmin(j_bart_simpson_test1)]
147
db['j_bart_simpson_test1'] = j_bart_simpson_test1
j_vraie_bart_simpson_test1 = [j_vraie(bart_simpson_test1,i) for i in mm] mm[argmin(j_vraie_bart_simpson_test1)]
148
db['j_vraie_bart_simpson_test1'] = j_vraie_bart_simpson_test1
On peut comparer les courbes avec :
plot(mm,j_bart_simpson_test1) plot(mm,j_vraie_bart_simpson_test1) ylim([-2.65,-2.5])
Construction de l'histogramme du jeu de données du Sloan Digital Sky Survey. Nous commençons par télécharger les données :
wget http://www.stat.cmu.edu/~larry/all-of-nonpar/=data/galaxy.dat
3.3.3.2 Construction d'une bande de confiance
Nous avons obtenu un estimateur \(\hat{f}_n(x)\) de \(f(x)\) de type histogramme en utilisant \(m\) classes de largeurs identique \(h = 1/m\) (on suppose que les données sont comprises entre 0 et 1 et on emploi une transformation linéaire si nécessaire). Nous définissons : \[\overline{f}(x) = \mathrm{E}\left(\hat{f}_n(x)\right) = \sum_{j=1}^m \frac{p_j}{h} \, I(x \in C_j) \, ,\] où \(p_j = \int_{C_j}\, f(x) \, dx\). \(\overline{f}(x)\) est une version constante par morceaux de \(f(x)\), sa valeur constante sur chaque classe est donnée par la moyenne de \(f\) sur cette classe.
Nous cherchons à présent une pair de fonctions \((b,h)\) générant une bande de confiance ayant une probabilité d'au moins \(1-\alpha\) de contenir \(\overline{f}(x)\) : \[\mathrm{Pr}\left\{b(x) \le \overline{f}(x) \le h(x), \; \forall \, x \right\} \ge 1 - \alpha \, .\]
La suite de comptes par classe \(\{Y_1,\ldots,Y_m\}\) peut être modélisée comme la réalisation d'une loi multinomiale à \(n\) tirages avec les probabilités \((p_1,\ldots,p_m)\) de tomber dans chaque classe. Supposons à présent que nos \(p_j\) sont assez petits pour que \(p_j (1 - p_j) \approx p_j\). Dit autrement, nous supposons que notre histogramme est « suffisamment fin » pour que la probabilité pour qu'une observation quelconque tombe dans n'importe laquelle des classes est par exemple \(\le 0,1\). Nous pouvons alors négliger la covariance entre les \(\hat{p}_j\) (\(\mathrm{Cov}(Y_i,Y_j) = - n p_i p_j\) soit \(\mathrm{Cov}(\hat{p}_i,\hat{p}_j) = - p_i p_j / n\)) et considérer les \(\hat{p}_j\) comme des tirages aléatoires de lois normales centrées sur \(p_j\) et de variances \(p_j/n\), ce que nous écrivons : \[\hat{p}_j \sim \mathcal{N}(p_j,p_j/n) \, ,\] ou encore \[\hat{p}_j = p_j + \sqrt{\frac{p_j}{n}} \, Z_j \quad \mathrm{où} \quad Z_j \sim \mathcal{N}(0,1) \, .\] Si maintenant nous considérons une nouvelle variable aléatoire \(\sqrt{\hat{p}_j}\) et si \(p_j/n\) et petit (hypothèse que nous avons déjà faite indirectement), nous pouvons effectuer un développement limité au premier ordre en \(\sqrt{p_j/n} \, Z_j\) pour obtenir : \[\sqrt{\hat{p}_j} = \sqrt{p_j + \sqrt{\frac{p_j}{n}} \, Z_j} \approx \sqrt{p_j} + \frac{1}{2} \, \frac{1}{\sqrt{p_j}} \, \sqrt{\frac{p_j}{n}} \, Z_j \, ,\] soit \[\sqrt{\hat{p}_j} \approx \sqrt{p_j} + \frac{1}{2 \, \sqrt{n}} \, Z_j \, .\]
Nous venons d'appliquer la propagation des incertitudes (ou propagation des erreurs, error propagation en anglais), méthode que les statisticien nomment méthode delta (la version des statisticiens est en fait un peu plus sophistiquée, dans son énoncé au moins). Nous l'avons employée ici pour stabiliser la variance ; nous sommes en effet passés d'une variable aléatoire \(\hat{p}_j\) dont la variance croît avec la moyenne, à une variable aléatoire \(\sqrt{\hat{p}_j}\) dont la variance est indépendante de la moyenne.
Nous remarquons que pouvons aussi écrire notre dernière équation de la façon suivante : \[2 \, \sqrt{n} \, \left(\sqrt{\hat{p}_j} - \sqrt{p_j}\right) \approx Z_j \, .\]
Nous allons chercher pour les fonctions basse (\(b(x)\)) et haute (\(h(x)\)) qui constituent les limites de notre bande de confiance une expression de la forme : \[\begin{array}{l l l} b(x) & = & \left(\max \left\{\sqrt{\hat{f}_n(x)} - c, 0\right\}\right)^2 \\ h(x) & = & \left(\sqrt{\hat{f}_n(x)} + c\right)^2\end{array}\]
Alors l'événement (au sens probabiliste du terme) \(\left\{b(x) \le \overline{f}(x) \le h(x), \; \forall \, x \right\}\) est identique à l'événement \(\left\{\sqrt{b(x)} \le \sqrt{\overline{f}(x)} \le \sqrt{h(x)}, \; \forall \, x \right\}\) puisque que les trois fonctions considérées sont positives ou nulles, d'où : \[\begin{array}{l l l l l l l} & & \max \left\{\sqrt{\hat{f}_n(x)} - c, 0\right\} & \le & \sqrt{\overline{f}(x)} & \le & \sqrt{\hat{f}_n(x)} + c \\ & & \max \left\{- c, - \sqrt{\hat{f}_n(x)} \right\} & \le & \sqrt{\overline{f}(x)} - \sqrt{\hat{f}_n(x)} & \le & c \\ -c & \le & \max \left\{- c, - \sqrt{\hat{f}_n(x)} \right\} & \le & \sqrt{\overline{f}(x)} - \sqrt{\hat{f}_n(x)} & \le & c \end{array}\] ce qui nous donne : \[\left\{b(x) \le \overline{f}(x) \le h(x), \; \forall \, x \right\} = \left\{\max_x \mid \sqrt{\hat{f}_n(x)} - \sqrt{\overline{f}(x)} \mid \le c \right\} \, .\] Si nous définissons à présent \(\hat{f}_{n,j} = \hat{f}_n(x)\) et \(\overline{f}_j = \overline{f}(x)\) pour \(x \in C_j\) notre événement peut s'écrire : \[\left\{b(x) \le \overline{f}(x) \le h(x), \; \forall \, x \right\} = \left\{\max_j \mid \sqrt{\hat{f}_{n,j}} - \sqrt{\overline{f}_j} \mid \le c \right\} \, .\]
Nous allons à présent considérer l'événement complémentaire de l'événement ci-dessus. Soit en utilisant les définitions de \(\hat{f}_{n}\) et \(\overline{f}\) : \[\begin{array}{l l l} \max_j \mid \sqrt{\hat{f}_{n,j}} - \sqrt{\overline{f}_j} \mid & > & c \\ \max_j \mid \sqrt{m} \left(\sqrt{\hat{p}_j} - \sqrt{p_j}\right) \mid & > & c \\ \max_j \mid \sqrt{\hat{p}_j} - \sqrt{p_j} \mid & > & \frac{c}{\sqrt{m}} \\ \max_j \; 2 \, \sqrt{n}\, \mid \sqrt{\hat{p}_j} - \sqrt{p_j} \mid & > & 2\, c \, \sqrt{\frac{n}{m}} \\ \max_j \; \mid Z_j \mid & > & 2 \, \sqrt{\frac{n}{m}} \, c \, .\end{array}\]
Nous avons donc : \[\mathrm{Pr}\left\{\max_j \; \mid Z_j \mid > 2 \, \sqrt{\frac{n}{m}} \, c\right\} \le \sum_{j=1}^m \mathrm{Pr}\left\{\mid Z_j \mid > 2 \, \sqrt{\frac{n}{m}} \, c\right\} = m \, \mathrm{Pr}\left\{\mid Z_j \mid > 2 \, \sqrt{\frac{n}{m}} \, c\right\} \, .\]
Si nous souhaitons avoir une probabilité d'au plus \(\alpha\) pour qu'en un point au moins \(\overline{f}(x)\) ne soit pas dans notre bande de confiance, il nous suffit de choisir \(c\) tel que : \[\mathrm{Pr}\left\{\mid Z_j \mid > 2 \, \sqrt{\frac{n}{m}} \, c\right\} = \frac{\alpha}{m} \, .\] Si nous notons : \[ z_{\alpha} = \Phi^{-1}(1-\alpha) \, , \] où \(\Phi\) désigne la fonction de répartition d'une variable aléatoire normale centrée, réduite (comme nos \(Z_j\)) et \(\Phi^{-1}\) désigne son inverse, la fonction percentile ; c'est-à-dire que nous avons : \[\begin{array}{l l l}\Phi(z_{\alpha}) & = & 1-\alpha \\ \mathrm{Pr}\left\{ Z_j \le z_{\alpha}\right\} & = & 1 - \alpha \\ \mathrm{Pr}\left\{ Z_j > z_{\alpha}\right\} & = & \alpha\end{array}\] et par symétrie de la loi normale : \(\mathrm{Pr}\left\{ Z_j < -z_{\alpha}\right\} = \alpha\). Donc \[\mathrm{Pr}\left\{ \mid Z_j \mid > z_{\alpha}\right\} = \mathrm{Pr}\left\{ Z_j > z_{\alpha}\right\} + \mathrm{Pr}\left\{ Z_j < - z_{\alpha}\right\} = 2 \, \alpha \; .\] Soit : \[\mathrm{Pr}\left\{ \mid Z_j \mid > z_{\alpha/2m}\right\} = \frac{\alpha}{m}\] et la condition : \[\mathrm{Pr}\left\{\mid Z_j \mid > 2 \, \sqrt{\frac{n}{m}} \, c\right\} = \frac{\alpha}{m}\] nous donne : \[2 \, \sqrt{\frac{n}{m}} \, c = z_{\alpha/2m} \] soit \[c = \frac{z_{\alpha/2m}}{2}\sqrt{\frac{m}{n}} \, .\]
Résumé: Avec \(c = \frac{z_{\alpha/2m}}{2}\sqrt{\frac{m}{n}}\) et les fonctions : \[\begin{array}{l l l} b(x) & = & \left(\max \left\{\sqrt{\hat{f}_n(x)} - c, 0\right\}\right)^2 \\ h(x) & = & \left(\sqrt{\hat{f}_n(x)} + c\right)^2\end{array} \, .\] Nous avons \[\mathrm{Pr}\left\{b(x) \le \overline{f}(x) \le h(x), \; \forall \, x \right\} \ge 1 - \alpha \, .\]
Appliquons ce résultat à notre histogramme précédent où nous avions obtenu \(m=77\) par validation croisée et où \(n=1000\). La fonction norm.ppf est la fonction percentile de Python. Si nous souhaitons une probabilité « d'être dans la bande » d'au moins 95 % nous devons donc prendre pour \(c\) :
c = norm.ppf(1-0.05/2/77)/2*sqrt(77./1000)
c
0.4731345039585666
D'où :
h = (sqrt(f_chapeau)+c)**2 b = sqrt(f_chapeau)-c b = clip(b,0,b) b = b**2 plot(cb[1:],f_chapeau,ls='steps') ylabel(u'Densité estimée') plot(cb[1:],b,ls='steps--') plot(cb[1:],h,ls='steps--')
db.close()
4 Estimation par maximisation de la vraisemblance
4.1 La fonction de vraisemblance
Soient \(\mathbf{X} = (X_1,\ldots,X_n)\) des variables aléatoires dont la densité ou la fonction de masse conjointe est \(f(\mathbf{x};\theta)\) avec \(\theta \in \Theta\). Étant données les observations \(\mathbf{X} = \mathbf{x}\), nous définissons la fonction de vraisemblance par : \[\mathcal{L}(\theta) \doteq f(\mathbf{x};\theta)\; .\] Pour chaque échantillon possible \(\mathbf{x} = (x_1,\ldots,x_n)\), la fonction de vraisemblance \(\mathcal{L}(\theta)\) est une fonction à valeurs réelles définie sur l'espace des paramètres. Remarquez que nous n'avons pas besoin de supposer que les \(X_1,\ldots,X_n\) sont de variables aléatoires indépendantes.
4.2 Estimateur du maximum de vraisemblance
Supposons que pour les observations \(\mathbf{x} = (x_1,\ldots,x_n)\), \(\mathcal{L}(\theta)\) est maximale, pour \(\theta \in \Theta\), en \(\theta = S(\mathbf{x})\) : \[\sup_{\theta \in \Theta} \mathcal{L}(\theta) = \mathcal{L}\left(S(\mathbf{x})\right)\] où \(S(\mathbf{x}) \in \Theta\). La statistique \(\hat{\theta} = S(\mathbf{X})\) est appelée estimateur du maximum de vraisemblance (EMV).
Il y a essentiellement deux méthodes pour trouver l'EMV:
- la « maximisation directe » : un examen de \(\mathcal{L}(\theta)\) donne la valeur de \(\theta\) qui maximise \(\mathcal{L}(\theta)\) étant données les observations \(x_1,\ldots,x_n\) ; cette méthode est utile lorsque que le domaine des données dépend du paramètre ;
- les « équations de vraisemblance » : lorsque le domaine des données ne dépend pas du paramètre, que l'espace du paramètre \(\Theta\) est un ensemble ouvert et que la fonction de vraisemblance est dérivable par-rapport à \(\theta = (\theta_1,\ldots,\theta_p)\) ; l'estimateur du maximum de vraisemblance \(\hat{\theta}\) est solutions des équations de vraisemblance :\[\frac{\partial}{\partial \theta_k} \ln \mathcal{L}(\hat{\theta}) = 0 \, ,\quad \mathrm{pour} \quad k = 1,\ldots,p \, .\]
La fonction \(\ln \mathcal{L}(\theta)\) est appelée fonction de log-vraisemblance.
4.2.1 Exemple : échantillon IID de loi uniforme
Supposons que les v.a. \(X_1,\ldots,X_n\) sont IID de loi uniforme continue sur l'intervalle \([0,\theta]\) pour un \(\theta > 0\). La fonction de vraisemblance est : \[\mathcal{L}(\theta) = \theta^{-n} I(0 \le x_1,\ldots,x_n \le \theta) = \theta^{-n} I\left(\theta \ge \max(x_1,\ldots,x_n)\right)\, .\] Donc \(\mathcal{L}(\theta) = 0\) si \(\theta < \max(x_1,\ldots,x_n)\) alors que \(\mathcal{L}(\theta)\) est strictement décroissante si \(\theta \ge \max(x_1,\ldots,x_n)\). Donc \(\mathcal{L}(\theta)\) est maximale en \(\theta = \max(x_1,\ldots,x_n)\) et : \[\hat{\theta} = X_{(n)} = \max(x_1,\ldots,x_n) \, .\]
4.2.2 Exemple : échantillon IID de loi de Poisson
Supposons que les v.a. \(X_1,\ldots,X_n\) sont IID de loi de Poisson de paramètre \(\lambda > 0\). La fonction de vraisemblance est : \[\mathcal{L}(\lambda) = \prod_{i=1}^n \frac{\lambda^{x_i} \, \exp(-\lambda)}{x_i!}\] et la log-vraisemblance est : \[\ln \mathcal{L}(\lambda) = -n \, \lambda + \ln(\lambda) \, \sum_{i=1}^n x_i - \sum_{i=1}^n \ln(x_i!) \, .\] En supposant \(\sum_{i=1}^n x_i > 0\) et en dérivant par-rapport à \(\lambda\) il vient : \[\frac{d}{d\lambda} \ln \mathcal{L}(\lambda) = -n + \frac{1}{\lambda} \sum_{i=1}^n x_i\] et la dérivée s'annule en \(\lambda = \overline{x}\). Nous vérifions maintenant que ce point correspond bien à un maximum en calculant la dérivée seconde : \[\frac{d^2}{d\lambda^2} \ln \mathcal{L}(\lambda) = - \frac{1}{\lambda^2} \sum_{i=1}^n x_i \, ,\] qui est toujours négative. La fonction de vraisemblance atteint donc son unique maximum en \(\overline{x}\) et l'EMV de \(\lambda\) est \(\hat{\lambda} = \overline{X}\), dès lors que \(\sum_{i=1}^n X_i > 0\). Si \(\sum_{i=1}^n X_i = 0\), l'EMV n'existe pas.
4.3 Pourquoi l'EMV est-il un estimateur « sensé » ?
Pour simplifier, supposons que \(X_1,\ldots,X_n\) sont des v.a. IID de densité (ou « fonction de masse ») \(f_0(x)\) et de fonction de répartition \(F_0(x)\). Alors, pour toute autre densité (ou fonction de masse) définie sur le même ensemble, nous pouvons définir la Divergence de Kullback-Leibler par : \[D(f_0,f) = \mathrm{E}_0\left[\ln\left(\frac{f_0(X_i)}{f(X_i)}\right)\right] \, ,\] où l'espérance \(\mathrm{E}_0\) est calculée avec \(X_i \sim F_0\). \(D(f_0,f)\) peut-être interprétée comme une « distance » entre la « vraie » densité (fonction de masse) \(f_0\) et une autre densité (fonction de masse) \(f\). On voit en effet facilement que : \[D(f_0,f_0) = 0 \, .\] Comme la fonction \(\ln\) est concave, l'inégalité de Jensen (qui se montre facilement par récurrence dans le cas des moyennes empiriques ou des loi discrètes) nous donne : \[D(f_0,f) = \mathrm{E}_0\left[\ln\left(\frac{f_0(X_i)}{f(X_i)}\right)\right] \ge \ln \mathrm{E}_0\left[\frac{f_0(X_i)}{f(X_i)}\right] = 0 \textrm{ car } f \textrm{ est une densité}\, .\] Ainsi la « fonctionnelle » (fonction de fonctions), \(D(f_0,f)\) (\(f_0\) est ici fixée et \(f\) varie dans un espace de fonctions adéquat) atteint sa valeur minimale en \(f=f_0\). De plus, à moins que \(f(x) = f_0(x)\) pour tout \(x\), \(D(f_0,f) > 0\) (ça je ne l'ai pas prouvé ici mais c'est vrai !).
Remarquons maintenant que : \[D(f_0,f) = -\mathrm{E}_0\left[\ln\left(f(X_i)\right)\right] + \mathrm{E}_0\left[\ln\left(f_0(X_i)\right)\right] \, ,\] donc pour \(f_0\) fixée, \[L(f_0,f) = \mathrm{E}_0\left[\ln\left(f(X_i)\right)\right]\] est maximale en \(f=f_0\). Or pour un échantillon IID, la loi des grands nombres nous donne : \[\hat{L}(f_0,f) = \frac{1}{n} \sum_{i=1}^n \ln f(X_i) \stackrel{P}{\rightarrow} \mathrm{E}_0\left[\ln\left(f(X_i)\right)\right] \, .\] Si \(\mathcal{F} = \{f(x;\theta) : \theta \in \Theta\}\) alors \(n \, \hat{L}(f_0,f)\) est la fonction de log-vraisemblance et choisir l'EMV revient à minimiser une approximation observable de la divergence de Kullback-Leibler. Comme cette approximation converge (dans le cas IID au moins) en probabilité vers la « vraie » divergence on peut espérer que si (par chance) \(f_0 = f(x;\theta_0) \in \mathcal{F}\) alors \(\hat{\theta} \stackrel{P}{\rightarrow} \theta_0\). On souhaiterez aussi, dans ces cas là, être aussi capable de dire quelque chose sur la loi de \(\hat{\theta}\).
4.4 Théorie asymptotique de l'EMV
Dans quelles conditions l'EMV converge-t-il et est-il un estimateur asymptotiquement normal d'un paramètre ? Dans les cas simples, comme celui de l'échantillon IID de loi de Poisson étudié ci-dessus, l'EMV est une fonction de la moyenne empirique. Alors, la loi des grands nombres, la convergence d'une fonction d'une variable aléatoire ,le théorème de Slutsky, le théorème central limite et la méthode delta (ou la propagation des incertitudes) nous permettent d'établir la convergence de l'EMV et sa normalité asymptotique. L'exemple qui va suivre devrait clarifier ces affirmations. Mais avant de le développer, nous allons rappeler la définition et l'utilisation de la fonction génératrice des moments.
4.4.1 Fonction génératrice des moments
La fonction génératrice des moments d'une variable aléatoire \(X\) est définie par : \[M_X(t) = \mathrm{E}\left(\exp(tX)\right),\quad |t| \le b > 0\, ,\] lorsque \(M_X(t) < \infty\).
Comme son nom l'indique, la fonction génératrice des moments est employée pour obtenir les moments de la v.a. \(X\) : \(\mathrm{E}\left(X\right), \mathrm{E}\left(X^2\right), \mathrm{E}\left(X^3\right), \ldots\). \(\mathrm{E}\left(X^k\right)\) est, par définition, le $k$-ième moment de \(X\). Nous avons alors le théorème suivant :
Théorème Soit \(X\) une variable aléatoire de fonction génératrice des moments \(M_X(t)\). Alors pour tout \(r > 0\), \(\mathrm{E}\left(|X|^r\right) < \infty\) et \(\mathrm{E}\left(X\right) = M'_X(0)\), \(\mathrm{E}\left(X^2\right) = M''_X(0)\) et plus généralement, \(\mathrm{E}\left(X^k\right) = M^{(k)}_X(0)\), où \(M^{(k)}_X\) désigne la $k$-ième dérivée de \(M_X\).
4.4.2 Échantillon de loi géométrique
Supposons que les v.a. \(X_1,\ldots,X_n\) sont IID de loi géométrique dont la fonction de masse est : \[f(x;\theta) = \theta \, (1-\theta)^{x-1}, \quad x=1,2,\ldots, \quad 0 < \theta < 1\; .\] Attention lors de la présentation du cours, j'ai suivi le bouquin de Keith Knight et utilisé une définition moins habituelle de la fonction de masse : \(f(x;\theta) = \theta \, (1-\theta)^x, \quad x=0,1,2,\ldots, \quad 0 < \theta < 1\). La suite est en fait plus simple avec la définition plus « classique ».
Vous pouvez « voir » à quoi cette loi correspond en considérant que \(\theta\) est la probabilité de gagner au tirage d'une loterie dont les tirages successifs sont indépendants et identiquement distribués, \(f(x;\theta)\) est alors la probabilité de gagner pour la première fois au $x$-ième tirage. Le nom de la loi vient de la série géométrique de raison \(q\), pour laquelle, si vous vous souvenez bien : \[\sum_{i=0}^{\infty} q^i = \frac{1}{1-q}, \quad |q| < 1 \; .\] En posant \(q = (1-\theta)\) vous voyez immédiatement que : \[\sum_{x=1}^{\infty} f(x;\theta) = 1\; .\]
Ici la vraisemblance de \(\theta\) étant donné \(X_1=x_1,\ldots,X_n=x_n\) s'écrie : \[\mathcal{L}(\theta) = \prod_{i=1}^n \theta \, (1-\theta)^{x_i-1}\] et la log-vraisemblance est : \[\mathcal{l}(\theta) = \log \mathcal{L}(\theta) = n\, \log(\theta) + \log(1-\theta) \, \sum_{i=1}^n (x_i-1) \; .\] En dérivant deux fois on établit que l'EMV de \(\theta\) est : \[\hat{\theta} = \frac{1}{\overline{X}_n} \; ,\] où \[\overline{X}_n \doteq \frac{1}{n} \sum_{i=1}^n X_i \; .\] L'EMV est ainsi une fonction continue de la moyenne empirique et nous avons : \[\overline{X}_n \stackrel{P}{\rightarrow} \mathrm{E}(X) \quad \textrm{(loi des grands nombres)} \, .\] Comme \(\hat{\theta} = g(\overline{X}_n)\) où \(g(x)=1/x\) est une fonction continue (pour \(x>0\), ce qui est le cas ici), la convergence d'une fonction d'une variable aléatoire nous donne : \[\hat{\theta} \stackrel{P}{\rightarrow} \frac{1}{\mathrm{E}(X)}\] ce qui prouve la convergence de l'EMV.
Le théorème central limite (TCL) nous permet d'affirmer que : \[\sqrt{n} \, \left(\overline{X}_n - \mathrm{E}(X)\right) \stackrel{L}{\rightarrow} \mathcal{N}(0,\sigma^2_X)\] si \(\sigma^2_X < \infty\) et la méthode delta que si \(g\) est dérivable telle que \(g'\left(\mathrm{E}(X)\right) \neq 0\) alors : \[\sqrt{n} \, \left(g\left(\overline{X}_n\right) - g\left(\mathrm{E}(X)\right)\right) \stackrel{L}{\rightarrow} \mathcal{N}\left[0,\sigma^2_X g'\left(\mathrm{E}(X)\right)^2\right] \, .\]
On pourra préférer écrire ces deux dernières équations : \[\overline{X}_n \stackrel{L}{\rightarrow} \mathrm{E}(X) + \frac{\sigma_X}{\sqrt{n}} \, Z\; ,\] où \(Z\) désigne une v.a. de loi normale centrée réduite et : \[g\left(\overline{X}_n\right) \stackrel{L}{\rightarrow} g\left(\mathrm{E}(X)\right) + |g'\left(\mathrm{E}(X)\right)|\,\frac{\sigma_X}{\sqrt{n}} \, Z\; .\]
Il nous reste donc à trouver \(\mathrm{E}(X)\) et \(\sigma_X\) pour \(X\) v.a. de loi géométrique de paramètre \(\theta\). Pour ce faire, nous pouvons, comme nous l'avons vu en cours, employer une méthode directe qui repose essentiellement sur l'identité :
\[S(\theta) = \sum_{x=1}^{\infty} \theta \, (1-\theta)^{x-1} = 1 \, ,\]
suivie d'une dériavtion par-rapport à \(\theta\) en interchangeant la dérivation avec la sommation, puis, après quelques manipulations, une identification. Clairement, cette méthode, si elle peut toujours être mise en œuvre, prend du temps et nous expose aux erreurs de calculs. Une autre solution est d'aller voir le site wikipédia de la loi géométrique où on trouvera :
\[\mathrm{E}(X) = 1/\theta \textrm{ et } \sigma_X = \sqrt{1-\theta}/\theta\, .\]
Faites attention ici à la convention adoptée lors de la définition de la loi (la « classique » avec l'indice qui commence à 1 ou celle, plus rare, de Knight dont l'indice commence à 0). Les « bons bouquins », comme ceux de Rice et Wasserman, ont une table des lois usuelles avec leurs propriétés comme la moyenne, l'écart type, etc…
On peut aussi faire appel au module SymPy de Python, module dédié à la résolution symbolique de problèmes mathématiques comme l'intégration, la différentiation, le calcul des limites, etc… Nous allons l'employer ici pour faire des calculs symboliques à partir de la fonction génératrice des moments, cette dernière est ici :
\[M_X(t) = \mathrm{E}\left(\exp(t X)\right) = \sum_{x=1}^{\infty} \exp(t x) \, \theta \, (1-\theta)^{x-1}\; ,\]
ce qui donne quasi immédiatement :
\[M_X(t) = \frac{\theta}{1-\theta} \sum_{x=1}^{\infty} \left(\exp(t) \, (1-\theta)\right)^x = \frac{\theta \, \exp t}{1 - \exp(t) \, (1-\theta)}\, \textrm{ pour } t < -\log(1-\theta)\; .\]
Nous définissons cette fonction génératrice des moments de la façon suivante — avec SymPy nous devons introduire des « variables symboliques » qui restent non-évaluées :
from sympy import * theta = Symbol('theta', real=True, positive=True) t = Symbol('t') M_X = theta * exp(t)/(1-exp(t)*(1-theta))
Si vous souhaitez ne pas importer tout l'espace de noms comme nous l'avons fait ici (avec from symport *) vous pouvez entrer quelque chose comme :
import sympy as sy theta = sy.Symbol('theta', real=True, positive=True) t = sy.Symbol('t') M_X = theta * sy.exp(t)/(1-sy.exp(t)*(1-theta))
Remarquez que nous appelons alors la version « symbolique » de l'exponentielle (sy.exp) et non la version numérique qui est appelée par défaut (exp). Il en va alors de même pour toutes les fonctions classiques qui constituent des expressions symboliques.
Pour obtenir la dérivée première nous utilisons la fonction diff (ou sy.diff si nous n'avons pas importé tout l'espace de noms) :
diff(M_X,t)
theta*(-theta + 1)*exp(2*t)/(-(-theta + 1)*exp(t) + 1)**2 + theta*exp(t)/(-(-theta + 1)*exp(t) + 1)
Quand les résultats sont « un peu longs », leur appliquer la fonction simplify est en général une bonne idée :
simplify(diff(M_X,t))
theta*exp(t)/((theta - 1)*exp(t) + 1)**2
Maintenant, pour obtenir la valeur de notre premier moment, nous devons remplacer t par 0 ou substituer 0 à t en langage de calcul symbolique. Cette opération est effectuée en appelant la méthode subs sur l'objet précédent, de la façon suivante :
simplify(diff(M_X,t)).subs(t,0)
1/theta
Ces opérations de substitutions constituent la base du calcul symbolique et vous êtes invités à lire le paragraphe du tutoriel qui s'y rapporte.
Remarque : les sorties les plus simples générées par SymPy sont montrées ici (de l'ASCII pur). Vous pouvez générer des sorties plus sophistiquées avec la commande :
init_printing()
Pour une description plus complète des différentes sorties (et sur comment les obtenir), consultez la page de la documentation correspondante.
La variance est le second moment auquel on soustrait le carré du premier (la moyenne), ce qu'on obtient avec :
simplify((diff(M_X,t,2)-diff(M_X,t,1)**2).subs(t,0))
(-theta + 1)/theta**2
En fin de compte, nous avions établi que : \[\hat{\theta} \stackrel{P}{\rightarrow} \frac{1}{\mathrm{E}(X)}\; ,\] or nous venons de voir que : \(\mathrm{E}(X) = 1/\theta\), ce qui nous donne : \[\hat{\theta} \stackrel{P}{\rightarrow} \theta \; .\] La loi normale asymptotique : \[\sqrt{n} \, \left(g\left(\overline{X}_n\right) - g\left(\mathrm{E}(X)\right)\right) \stackrel{L}{\rightarrow} \mathcal{N}\left[0,\sigma^2_X g'\left(\mathrm{E}(X)\right)^2\right] \, ,\] devient, en utilisant le fait que \(g(x) = 1/x\) et \(g'(x) = -1/x^2\) (attention il faut prendre ici \(x = 1/\theta\)): \[\sqrt{n} \, \left(\hat{\theta} - \theta\right) \stackrel{L}{\rightarrow} \mathcal{N}\left[0,(1-\theta) \, \theta^2\right] \, .\]
Il peut être intéressant à ce stade de comparer l'approximation asymptotique ci-dessus avec la distribution exacte puisque cette dernière est disponible. En effet, notons \(T = \sum_{i=1}^s X_i\), où les \(X_i\) sont des v.a. IID de loi géométrique de paramètre \(\theta\). Nous avons clairement : \(\overline{X}_s = T/s\). Pour que \(T=t\) il faut que parmi les \(t-1\) tirages qui précèdent, nous aillons \(s-1\) « succès ». Rappelez-vous que chaque tirage suivant une loi géométrique de paramètre \(\theta\) peut être vu comme une suite de \(x\) tirages IID suivant une loi de Bernoulli pour laquelle \(\theta\) est la probabilité de succès et où \(x=1,2,\ldots\) est la tirage pour lequel le premier succès est observé. Ainsi, \(s\) tirages indépendants suivant une loi géométriques peuvent être vus comme une suite de tirages de suivant une loi de Bernoulli jusqu'à ce que le $s$-ième succès soit observé. On obtient ainsi la fonction de masse de la v.a. \(T\) : \[\mathrm{Pr}\{T=t\} = {t-1 \choose s-1}\theta^s \, (1-\theta)^{t-s} \; , \quad t = s,s+1,\ldots\] La v.a. \(T\) suit une loi binomiale négative de paramètres \(s=1,2,\ldots\) et \(0<\theta<1\) (on peut en fait généraliser la définition à tout \(n>0\) réel en utilisant la fonction gamma à la place des factoriels dans l'équation précédente). Attention : la loi est parfois définie (comme sur le site wikipédia, où vous trouverez aussi une explication du nom de la loi) comme donnant la probabilité du nombre d'échecs observés jusqu'au $s$-ième succès, on a alors : \[\mathrm{Pr}\{E=e\} = {s+e-1 \choose s-1}\theta^s \, (1-\theta)^{e} \; , \quad e=0,1,\ldots \; ,\] les paramètres de la loi sont les mêmes qu'avec la définition précédente.
La convergence en loi que nous pouvons réécrire :
\[\sqrt{\frac{n}{(1-\theta) \, \theta^2}} \, \left(\hat{\theta} - \theta\right) \stackrel{L}{\rightarrow} \mathcal{N}\left(0,1\right) \, ,\]
nous dit que la fonction de répartition de la v.a. :
\[\hat{\eta}_n \doteq \sqrt{\frac{n}{(1-\theta) \, \theta^2}} \, \left(\hat{\theta} - \theta\right)\; ,\]
(je rajoute l'indice pour garder trace de la taille de l'échantillon) admet pour limite quand \(n\) tend vers l'infini, la fonction de répartition d'une loi normale centrée réduite. Mais \(\hat{\theta}_n = n/T_n\) donc :
\[\begin{array}{l,l,l} F_{\hat{\theta}_n}(x) & = & \mathrm{Pr}\{\hat{\theta}_n \le x\} \textrm{ définition de la fonction de répartition,}\\ & = & \mathrm{Pr}\{n/T_n \le x\} \textrm{ définition de l'EMV,} \\ & = & \mathrm{Pr}\{T_n \ge n/x\} \, .\end{array}\]
Et \(T_n\) le nombre total de tirages de Bernoulli jusqu'à l'obtention du $n$-ième succès peux aussi s'écrire : \(T_n = E_n + n\), où \(E_n\) est le nombre d'échecs jusqu'au $n$-ième succès, d'où :
\[\begin{array}{l,l,l} F_{\hat{\theta}_n}(x) & = & \mathrm{Pr}\{T_n \ge n/x\} \\ & = & \mathrm{Pr}\{E_n + n \ge n/x\} \\ & = & \mathrm{Pr}\{E_n \ge n/x - n\} \\ & = & 1 - \mathrm{Pr}\{E_n \le n/x - n\} \\ & = & 1 - F_{E_n}\left(n/x - n\right)\, .\end{array}\]
J'ai fait toute cette « gymnastique » par-ce que le site wikipédia me dit que la fonction de répartition d'une loi binomiale négative est une fonction bêta incomplète régularisée, c'est-à-dire que :
\[F_{E_n}(y;n,\theta) = I_{\theta}(n,y+1) = \frac{\int_0^{\theta}t^{n-1} (1-t)^y dt}{\int_0^{1}t^{n-1} (1-t)^y dt} \; .\]
« Heureusement » pour nous, le sous module special de scipy contient cette fonction et nous pouvons définir ainsi une fonction Python qui renvoie la valeur de la fonction de répartition de notre \(\hat{\theta}_n\) de la façon suivante (de ce qui suit, comme d'habitude, je suppose que vous utilisez IPython et que la commande magique %pylab a été exécutée) :
from scipy.special import betainc def F_theta_hat(x,n,theta): return 1-betainc(n,n/x-n,theta)
Nous obtenons maintenant facilement, la fonction de répartition de \(\hat{\eta}_n\) (qui doit être asymptotiquement normale, centrée, réduite) à partir de celle de \(\hat{\theta}\) et de la définition de \(\hat{\eta}_n\) : \[\begin{array}{l,l,l} F_{\hat{\eta}_n}(x) & = & \mathrm{Pr}\{\hat{\eta}_n \le x\} \\ & = & \mathrm{Pr}\left\{\sqrt{\frac{n}{(1-\theta) \, \theta^2}} \, \left(\hat{\theta}_n - \theta\right) \le n/x \right\} \\ & = & \mathrm{Pr}\left\{\hat{\theta}_n \le \theta \, \sqrt{\frac{1-\theta}{n}}\, x + \theta \right\} \\ & = & F_{\hat{\theta}_n}\left(\theta \, \sqrt{\frac{1-\theta}{n}}\, x + \theta\right)\, .\end{array}\]
D'où la définition de notre fonction de répartition en Python :
def F_eta_hat(x,n,theta): return F_theta_hat(theta*(sqrt((1-theta)/n)*x+1),n,theta)
4.4.2.1 Comparaisons entre fonctions de répartition exactes et limites asymptotiques
Pour plus de clarté, nous allons traçer les différences entre les fonctions de répartition exactes et leur limite asymptotique (loi normale centrée réduite), dans deux cas :
- la vraie valeur de \(\theta = 0.5\) avec trois tailles d'échantillons : 20, 200, 2000 ;
- la vraie valeur de \(\theta = 0.1\) avec trois tailles d'échantillons : 40, 400, 4000.
from scipy.stats import norm yy = linspace(-3,3,601) subplot(121) plot(yy,[F_eta_hat(y,20,0.5) for y in yy]-norm.cdf(yy),lw=2,color='black') plot(yy,[F_eta_hat(y,200,0.5) for y in yy]-norm.cdf(yy),lw=2,color='black',ls='--') plot(yy,[F_eta_hat(y,2000,0.5) for y in yy]-norm.cdf(yy),lw=2,color='grey') ylim([-0.04,0]) legend(('n=20','n=200','n=2000'),loc='upper left',bbox_to_anchor=(0.4,0.3),frameon=False) ylabel('$F_{\hat{\eta}} - F_Z$') xlabel('$\hat{\eta}$') title('$ \\theta = 0.5 $') subplot(122) plot(yy,[F_eta_hat(y,40,0.1) for y in yy]-norm.cdf(yy),lw=2,color='black') plot(yy,[F_eta_hat(y,400,0.1) for y in yy]-norm.cdf(yy),lw=2,color='black',ls='--') plot(yy,[F_eta_hat(y,4000,0.1) for y in yy]-norm.cdf(yy),lw=2,color='grey') ylim([-0.04,0]) legend(('n=40','n=400','n=4000'),loc='lower center',bbox_to_anchor=(0.4,0.52),frameon=False) xlabel('$\hat{\eta}$') title('$ \\theta = 0.1 $')
Text(0.5,1,'$ \\theta = 0.1 $')
savefig('img/coursIntroStats2014/comparaison-fct-repartition-exacte-vs-limite-asymptotique-loi-geometrique.png') close() 'img/coursIntroStats2014/comparaison-fct-repartition-exacte-vs-limite-asymptotique-loi-geometrique.png'
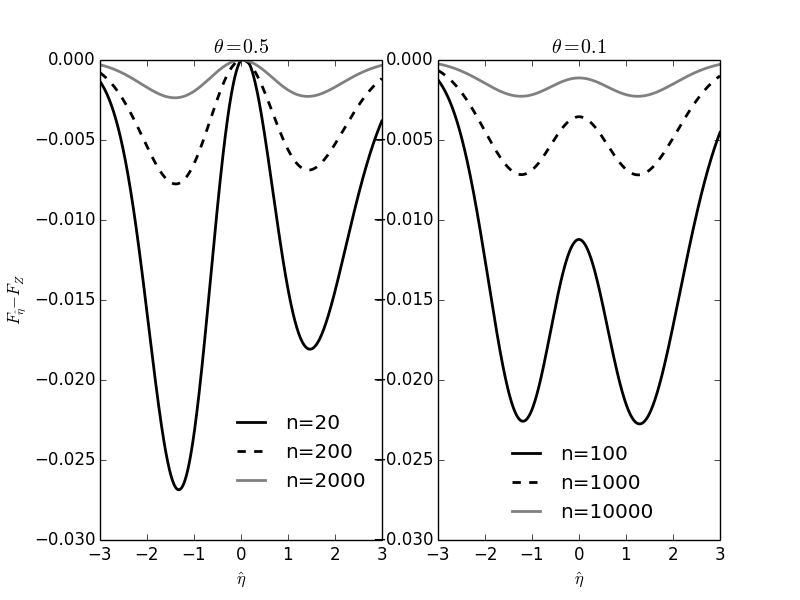
Figure 6 : Comparaisons des fonctions de répartition exactes et de leur limite asymptotique (loi normale centrée réduite) dans le cas d'une loi géométrique de paramètre \(\theta\). C'est la fonction de répartition de \(\hat{\eta}\), une version centrée et réduite, de l'EMV \(\hat{\theta}\) qui est considérée (voir le texte ci-dessus). Pour plus de clarté, la limite asymptotique a été soustraite de la valeur exacte (c.-à-d. que quand on a convergé, les courbes doivent être uniformément à 0).
Comme on peut s'y attendre, puisqu'à taille d'échantillon \(n\) fixée, la variance de \(\hat{\theta}\) est \(\sigma_{\hat{\theta}}^2 = (1-\theta) \theta^2/n\), on observe une convergence à peu près deux fois plus rapide avec \(\theta=0.5\) (\(\sigma_{\hat{\theta}}^2 = 0.125/n\)) qu'avec \(\theta=0.1\) (\(\sigma_{\hat{\theta}}^2 = 0.225/n\)).
4.4.3 Convergence en loi vers la « bonne valeur » du paramètre
Théorème Soient \(X_1,\ldots,X_n\) des v.a. IID de densité (ou « fonction de masse ») \(f_0 = f(x;\theta_0) \in \mathcal{F}\) où \(\mathcal{F} = \{f(x;\theta) : \theta \in \Theta\}\) est notre ensemble de densités « candidates ». Définissons : \[M_n(\theta) \doteq \frac{1}{n} \sum_{i=1}^{n} \ln \frac{f(X_i;\theta)}{f(X_i;\theta_0)}\] et \[M(\theta) \doteq \mathrm{E}_0\{\ln \frac{f(X_i;\theta)}{f(X_i;\theta_0)}\} = -D(\theta_0,\theta) \; .\] Si \[\sup_{\theta \in \Theta}|M_n(\theta) - M(\theta)| \stackrel{P}{\rightarrow} 0\] et si pour tout \(\epsilon > 0\), \[\sup_{\theta : |\theta - \theta_0 | \ge \epsilon} M(\theta) < M(\theta_0) \; ,\] alors : \(\hat{\theta} \stackrel{P}{\rightarrow} \theta_0\), où \(\hat{\theta}\) désigne l'EMV.
Preuve Par définition de \(\hat{\theta}\), \(M_n(\theta)\) est maximale en \(\hat{\theta}_n\) donc \(M_n(\hat{\theta}_n) \ge M_n(\theta_0)\). D'où \[\begin{array}{l,l,l} M(\theta_0) - M(\hat{\theta}_n) & = & M_n(\theta_0) - M(\hat{\theta}_n) + M(\theta_0) - M_n(\theta_0) \, , \\ & \le & M_n(\hat{\theta}_n) - M(\hat{\theta}_n) + M(\theta_0) - M_n(\theta_0) \, , \\ & \le & \sup_{\theta \in \Theta} |M_n(\theta) - M(\theta)| + M(\theta_0) - M_n(\theta_0) \, , \\ & \stackrel{P}{\rightarrow} & 0 \, .\end{array}\] Ainsi, quelque soit \(\delta > 0\) : \[\mathrm{Pr}\left\{M(\hat{\theta}_n) < M(\theta_0) - \delta \right\} \rightarrow 0 \; .\] Choisissons un \(\epsilon > 0\) quelconque. Notre dernière hypothèse nous dit qu'il existe un \(\delta > 0\), tel que \(|\theta - \theta_0| \ge \epsilon\) implique \(M(\theta) < M(\theta_0) - \delta\). Donc \[\mathrm{Pr}\left\{|\hat{\theta}_n - \theta_0| \ge \epsilon\right\} \le \mathrm{Pr}\left\{M(\hat{\theta}_n) < M(\theta_0) - \delta \right\} \rightarrow 0 \; .\] Ce qui complète la preuve.
Remarques :
- lors du cours, nous avons vu une condition un peu moins générale que la seconde hypothèse ci-dessus (qui revient à supposer l'existence d'un maximum global à l'intérieur de \(\Theta\)) pour la convergence puisque, suivant le bouquin de Keith Knight, nous avions supposé que la suite de fonctions \(M_n\) était une suite de fonctions concaves (j'ai suivi ici le bouquin de Wasserman) ;
- pour pouvoir appliquer le théorème, il faut vérifier une condition stochastique (convergence uniforme des \(M_n\) vers \(M\)), mais cette condition est relativement facile à vérifier dès lors que les données sont IID, il faut vérifier ensuite une condition déterministe, qui dans le cas d'un paramètre scalaire peut se faire en construisant le graphe de la fonction.
4.4.4 Loi asymptotique de l'EMV
Pour \(f(X;\theta)\) une densité de probabilité (ou fonction de masse), on note dans la suite \(l(X;\theta) = \ln f(X;\theta)\) et \(l'\), \(l''\) et \(l'''\) désignent respectivement les dérivées première, seconde et troisième par-rapport à \(\theta\).
Théorème Soient \(X_1,\ldots,X_n\) des v.a. IID de densité (ou « fonction de masse ») \(f_0 = f(x;\theta_0) \in \mathcal{F}\) où \(\mathcal{F} = \{f(x;\theta) : \theta \in \Theta\}\) est notre ensemble de densités « candidates ». Si
- \(\hat{\theta}_n \stackrel{P}{\rightarrow} \theta_0\) ;
- \(\hat{\theta}_n\) est tel que \(\sum_i l'(X_i,\hat{\theta}_n) = 0\) (solution des équations de vraisemblance).
Si
- l'espace des paramètres \(\Theta\) est un sous-ensemble ouvert de \(\mathbb{R}\) ;
- l'ensemble \(A = \{x : f(x;\theta) > 0\}\) ne dépend pas de \(\theta\) ;
- \(f(x;\theta)\) est trois fois continument différentiable par-rapport à \(\theta\) pour tout \(x \in A\) ;
- \(\mathrm{E}_{\theta}\left[l'(X_i;\theta)\right] = 0\) \(\forall\, \theta\) et \(\mathrm{Var}_{\theta}\left[l'(X_i;\theta)\right] = I(\theta)\) où \(0 < I(\theta) < \infty\), \(\forall\, \theta\) ;
- \(\mathrm{E}_{\theta}\left[l''(X_i;\theta)\right] = -J(\theta)\) où \(0 < J(\theta) < \infty\), \(\forall\, \theta\) ;
- \(\forall\, \theta\) et \(\delta > 0\), \(|l'''(X_i;t)| \le M(X_i)\) pour \(|t - \theta| \le \delta\) où \(\mathrm{E}_{\theta}\left[M(X_i)\right]< \infty\).
Alors \[\sqrt{n}\left(\hat{\theta}_n - \theta_0\right) \stackrel{L}{\rightarrow} \mathcal{N}\left(0,I(\theta_0)/J^2(\theta_0) \right)\, .\] Quand \(I(\theta_0) = J(\theta_0)\) nous avons : \(\sqrt{n}\left(\hat{\theta}_n - \theta_0\right) \stackrel{L}{\rightarrow} \mathcal{N}\left(0,1/I(\theta_0) \right)\).
Preuve Je ne la reproduit pas ici ; celle donnée en cours suivait le bouquin de Knight.
4.5 Une théorème dont le hypothèses sont plus faibles
Les deux théorèmes que nous venons d'énoncer peuvent être un peu difficile à employer car les conditions à du premier (sur la convergence de l'EMV) ne sont pas toujours simples à vérifier. Nous présentons donc un théorème dont les hypothèses sont plus faibles mais qui ne garantit pas la convergence de l'EMV vers « \(\theta_0\) », il garantit seulement la convergence de l'EMV vers une racine des équations de vraisemblance (ainsi que la normalité asymptotique de l'EMV).
Théorème Soient \(X_1,\ldots,X_n\) des v.a. IID de densité (ou « fonction de masse ») \(f_0 = f(x;\theta_0) \in \mathcal{F}\) où \(\mathcal{F} = \{f(x;\theta) : \theta \in \Theta\}\) est notre ensemble de densités « candidates » et où \(\Theta\) est un ouvert de \(\mathbb{R}\). Si
- (R1)
- pour tout \(\theta \in \Theta\), les dérivées : \[\frac{\partial \log f(x;\theta)}{\partial \theta}, \; \frac{\partial^2 \log f(x;\theta)}{\partial \theta^2}, \; \frac{\partial^3 \log f(x;\theta)}{\partial \theta^3}\] existent pour tout \(x\) ;
- (R2)
- pour tout \(\theta_0 \in \Theta\) il existe des fonctions \(g(x)\), \(h(x)\) et \(H(x)\) (dépendants potentiellement de \(\theta_0\)) telles que pour tout \(\theta\) dans un voisinage \(V(\theta_0)\) les relations : \[\left| \frac{\partial f(x;\theta)}{\partial \theta} \right| \le g(x), \; \left| \frac{\partial^2 f(x;\theta)}{\partial \theta^2} \right| \le h(x), \; \left| \frac{\partial^3 \log f(x;\theta)}{\partial \theta^3} \right| \le H(x)\] sont vérifiées et : \[\int g(x) dx < \infty, \; \int h(x) dx < \infty, \; \mathrm{E}_{\theta}\left( H(x) \right) < \infty \textrm{ pour } \theta \in V(\theta_0)\, ;\]
- (R3)
- pour tout \(\theta \in \Theta\) : \[0 < \mathrm{E}_{\theta}\left\{ \left(\frac{\partial \log f(x;\theta)}{\partial \theta}\right)^2 \right\} < \infty;\]
alors les équations de vraisemblances admettent une suite de solutions \(\{\hat{\theta}_n\}\) telle que : \[ \lim_{n \rightarrow \infty} \hat{\theta}_n = \theta \] et \[\hat{\theta}_n \stackrel{L}{\rightarrow} \mathcal{N}\left(\theta,\frac{1}{n \, \mathrm{E}_{\theta}\left\{ \left(\partial \log f(x;\theta)/\partial \theta\right)^2 \right\}}\right) \, .\]
Remarques Les conditions (R1) permettent un développement de Taylor de \(\partial \log f(x;\theta) / \partial \theta\) considérée comme fonction de \(\theta\) pour tout \(x\). Les conditions (R2) permettent de dériver \(\int f(x;\theta) dx\) et \(\int \partial \log f(x;\theta) / \partial \theta dx\) par-rapport à θ sous le signe somme. Condition (R3) signifie que la variable aléatoire \(\partial \log f(x;\theta) / \partial \theta\) a une variance strictement positive et finie.
Preuve Voir le bouquin de Serfling (1980) (p 144-148) 2.
4.5.1 Exemple : échantillon IID de loi de Cauchy
Supposons que \(X_1,X_2,\ldots,X_n\) sont IID de loi de Cauchy dont nous écrirons la densité : \[f(x;\theta) = \frac{1}{\pi} \frac{1}{1+(x-\theta)^2}\; .\] La fonction de log-vraisemblance est alors : \[\mathcal{l}(\theta) = - n \log \pi - \sum_{i=1}^n \log \left(1+(\theta-X_i)^2\right) \, .\] L'équation de vraisemblance devient : \[\frac{d \mathcal{l}}{d \theta} (\hat{\theta}_n) = \sum_{i=1}^n \frac{2 \, (X_i - \hat{\theta}_n)}{1+(\hat{\theta}_n-X_i)^2} = 0 \, .\]
La loi de Cauchy est l'exemple type d'une loi « pathologique » dans la mesure où aucun de ses moments n'est défini. C'est en fait aussi un exemple assez pathologique pour la méthode du maximum de vraisemblance comme l'a montré Barnett (1966)3. Ici nous allons essentiellement faire ce que les gens ne font presque jamais (et par là comprendre pourquoi les gens ne le font presque jamais), c'est-à-dire vérifier que les hypothèses nécessaires à l'application de nos théorèmes sont remplies. Nous allons ici utiliser le dernier théorème et vérifier les trois « conditions de régularité », (R1), (R2) et (R3).
La première se vérifie facilement en calculant les dérivées par-rapport à \(\theta \in \Theta \equiv \mathbb{R}\) et en vérifiant quelles sont finies pour tout \(x\). Avec SymPy (que je charge de façon à ce qu'il interragisse bien avec pylab, c'est-à-dire en gardant un espace de noms séparé pour SymPy) cela donne :
import sympy as sy x, theta = sy.symbols('x,theta', real=True) f = 1/(1+(theta-x)**2)/sy.pi
La dérivée première du log de la densité est :
sy.simplify(sy.diff(sy.log(f),theta))
2*(-theta + x)/((theta - x)**2 + 1)
La seconde :
sy.simplify(sy.diff(sy.log(f),theta,2))
2*((theta - x)**2 - 1)/((theta - x)**2 + 1)**2
La troisième :
sy.simplify(sy.diff(sy.log(f),theta,3))
-4*(theta - x)*((theta - x)**2 - 3)/((theta - x)**2 + 1)**3
Où on voit quelles sont toutes définies pour \(x, \theta \in \mathbb{R}\) ce qui vérifie (R1).
Pour vérifier (R2), il faut travailler un peu plus… Tout d'abord nous allons chercher une fonction \(g\) qui domine la norme de la dérivée de la densité (dans un voisinage d'une racine de l'équation de vraisemblance) et qui est intégrable. La dérivé première de la densité est :
sy.simplify(sy.diff(f,theta))
2*(-theta + x)/(pi*((theta - x)**2 + 1)**2)
Si \(\theta_0\) est une solution de l'équation de vraisemblance et si nous considrons un voisinage du type \(V(\theta_0) = (\theta_0-\delta,\theta_0+\delta)\) où \(\delta > 0\), alors, pour \(|x-\theta_0| < \delta\), \(|-\theta +x| \le 2 \delta\). Pour \(x-\theta_0 \ge \delta\) nous voyons que \(\partial f(x;\theta) / \partial \theta \le 2 (x + \delta - \theta_0) / (\pi ((x - \delta - \theta_0)^2+1)^2)\) ; ainsi : \[g(x) = \left\{\begin{array}{l l} \frac{2 (-x + \delta + \theta_0)}{\pi ((x - \delta - \theta_0)^2+1)^2} & \quad \text{si} \quad -x+\theta_0 \le -\delta \\ 2 \delta & \quad \text{si} \quad |x-\theta_0| < \delta \\ \frac{2 (x + \delta - \theta_0)}{\pi ((x - \delta - \theta_0)^2+1)^2} & \quad \text{si} \quad x-\theta_0 \ge \delta \end{array} \right.\] domine la valeur absolue de la dérivée première pour tout \(\theta \in V(\theta_0)\) et est clairement intégrable sur \(\mathbb{R}\).
Quand on fait ce genre de calcul, il peut être prudent de faire quelques graphes afin de vérifier que notre fonction dominante, domine bien ce qu'elle est sensée dominer… On pourra le faire ici de la façon suivante (les graphes ne sont pas montrés dans ce document) :
xx = linspace(-5,5,501) def abs_df(x,theta): """Renvoie la valeur absolue de la derivee premiere de la densite""" return abs(2*(-theta + x)/(pi*((theta - x)**2 + 1)**2)) def g(x,delta,theta0=0): """Renvoie une fonction dominant abs_df sur un voisinage de longueur delta autour de theta0""" if abs(x-theta0) < delta: return 2*delta else: return 2*(abs(x-theta0)+delta)/pi/((abs(x-theta0)-delta)**2+1)**2 plot(xx,[abs_df(x,0) for x in xx],color='black') plot(xx,[abs_df(x,0.5) for x in xx],color='black') plot(xx,[abs_df(x,-0.5) for x in xx],color='black') plot(xx,[g(x,0.5) for x in xx],color='red')
La dérivé seconde de la densité est :
sy.simplify(sy.diff(f,theta,2))
2*(3*(theta - x)**2 - 1)/(pi*((theta - x)**2 + 1)**3)
On voit alors que : \[h(x) = \left\{\begin{array}{l l} \frac{6 (|x-\theta_0| + \delta)^2}{\pi ((|x - \theta_0| - \delta )^2+1)^3} & \quad \text{si} \quad |x-\theta_0| \ge 1/\sqrt{3} \\ 2 / \pi & \quad \text{si} \quad |x-\theta_0| < 1/\sqrt{3} \end{array} \right.\] domine la valeur absolue de la dérivée seconde et est intégrable.
On peut encore vérifier graphiquement qu'on ne sait pas trompé avec :
def abs_ddf(x,theta): """Renvoie la valeur absolue de la derivee seconde de la densite""" return abs(2*(3*(theta - x)**2 - 1)/(pi*((theta - x)**2 + 1)**3)) def h(x,delta,theta0=0): """Renvoie une fonction dominant abs_ddf sur un voisinage de longueur delta autour de theta0""" if abs(x-theta0) < 1/sqrt(3): return 2/pi else: return 6*(abs(x-theta0)+delta)**2/pi/((abs(x-theta0)-delta)**2+1)**3 plot(xx,[abs_ddf(x,0) for x in xx],color='black') plot(xx,[abs_ddf(x,0.5) for x in xx],color='black') plot(xx,[abs_ddf(x,-0.5) for x in xx],color='black') plot(xx,[h(x,0.5) for x in xx],color='red') plot(xx,[h(x,sqrt(3)) for x in xx],color='blue')
La dérivée troisième du log de la densité est :
sy.simplify(sy.diff(sy.log(f),theta,3))
-4*(theta - x)*((theta - x)**2 - 3)/((theta - x)**2 + 1)**3
Si nous choisissons \(V(\theta_0) = (\theta_0 - \sqrt{3},\theta_0 + \sqrt{3})\), choix compatible avec les deux cas précédents, alors : \[H(x) = \left\{\begin{array}{l l} \frac{4 (|x-\theta_0| + \sqrt{3})}{((|x - \theta_0| - \sqrt{3})^2+1)^2} & \quad \text{si} \quad |x-\theta_0| \ge \sqrt{3} \\ 12 \sqrt{3} & \quad \text{si} \quad |x-\theta_0| < \sqrt{3} \end{array} \right.\] domine la valeur absolue de la dérivée troisième du log de la densité. Il nous reste à montrer que l'espérance de \(H(x)\) par-rapport à toute densité \((\pi (1+(\theta - x)^2))^{-1}\) où \(\theta \in (\theta_0 - \sqrt{3},\theta_0 + \sqrt{3})\) existe. Remarquez, pour les quelques calculs qui restent, que nous avons une invariance par translation (c'est toujours la différence \(x - \theta_0\) qui apparaît) et nous pouvons ainsi poser \(\theta_0 = 0\). Alors le morceau central de \(H(x)\) (pour \(x < \sqrt{3}\)) ne pose pas de problème d'intégration par-rapport à la densité. Il nous faut considérer les deux morceaux (principaux) symétriques, celui de droite étant : \[\int_{\sqrt{3}}^{\infty} \frac{4 (x + \sqrt{3})}{((x - \sqrt{3})^2+1)^2} \frac{1}{\pi (1+(\theta - x)^2)} dx \, ,\] où \(\theta \in (-\sqrt{3},\sqrt{3})\). Mais on a clairement : \[\int_{\sqrt{3}}^{\infty} \frac{4 (x + \sqrt{3})}{((x - \sqrt{3})^2+1)^2} \frac{1}{\pi (1+(\theta - x)^2)} dx \le \int_{\sqrt{3}}^{\infty} \frac{4 (x + \sqrt{3})}{((x - \sqrt{3})^2+1)^2} \frac{1}{\pi (1+(\sqrt{3} - x)^2)} dx \le \frac{4}{\pi} \int_{\sqrt{3}}^{\infty} \frac{x + \sqrt{3}}{(x - \sqrt{3})^6+1} dx\] et cette dernière intégrale vaut :
x = sy.symbols('x',real=True) sy.simplify(4/sy.pi*sy.integrate((x+sy.sqrt(3))/(1+(x-sy.sqrt(3))**6),(x,sy.sqrt(3),sy.oo)))
28*sqrt(3)/9
Et on vérifie graphiquement que cela colle avec :
def abs_dddlogf(x,theta): """Renvoie la valeur absolue de la derivee troisieme de la log densite""" return abs(-4*(theta - x)*((theta - x)**2 - 3)/((theta - x)**2 + 1)**3) def H(x,theta0=0): """Renvoie une fonction dominant abs_dddlogf sur un voisinage de longueur sqrt(3) autour de theta0""" if abs(x-theta0) < sqrt(3): return 12*sqrt(3) else: return 4*(abs(x-theta0)+sqrt(3))/((abs(x-theta0)-sqrt(3))**2+1)**2 plot(xx,[abs_dddlogf(x,0) for x in xx],color='black') plot(xx,[abs_dddlogf(x,1) for x in xx],color='black') plot(xx,[abs_dddlogf(x,sqrt(3)) for x in xx],color='black') plot(xx,[abs_dddlogf(x,-1) for x in xx],color='black') plot(xx,[abs_dddlogf(x,-sqrt(3)) for x in xx],color='black') plot(xx,[H(x) for x in xx],color='red')
Ce qui achève la vérification de (R2).
Grâce à SymPy, vérifier (R3) est un jeu d'enfant, puisque nous obtenons l'expression analytique de l'espérance du carré de la dérivé première (par-rapport au paramètre) du log de la densité avec :
x = sy.symbols('x',real=True) sy.simplify(sy.integrate(sy.diff(sy.log(f),theta)**2*f,(x,-sy.oo,sy.oo)))
1/2
4.6 Intervalles de confiance
La méthode du maximum de vraisemblance que nous venons d'exposer, nous donne (dans les cas où elle s'applique) un estimateur qu'on peut montrer être optimal4. Mais, résumer des expériences et leur analyse par un seul nombre, fut-il « optimal » comme l'EMV n'est pas suffisant ! Nous avons en effet établi la loi asymptotique de l'EMV qui, à taille d'échantillon finie — qui est la seule taille atteignable en ce bas Monde — ne se réduit pas à une masse unité concentrée en un point ; cela signifie pratiquement que si nous (ou des collègues d'un autre laboratoire) reproduisons les mêmes expériences dans les mêmes conditions, nous n'aurons pas deux fois la même valeur de l'EMV. Les valeurs seront différentes et ce dont nous avons besoin, c'est d'un « mètre étalon » qui nous permette de dire si deux valeurs estimées pour le (ou les) même(s) paramètre(s) sont suffisamment proches pour être compatibles ou non. Nous en arrivons ainsi à la notion d'intervalle de confiance. L'idée clé est que nous n'allons pas rapporté la valeur de l'EMV, mais plutôt les bornes d'un intervalle incluant l'EMV et ayant une probabilité minimale donnée de contenir la vraie valeur du paramètre. Nous sommes contraints à fixer une probabilité (qui en générale sera plus petite que 1) pour les mêmes raisons qui font que notre EMV est la réalisation d'une variable aléatoire : les bornes de nos intervalles de confiance vont être des fonctions de nos échantillons et vont ainsi être elles aussi des réalisations de variables aléatoires. On s'attend dès lors à ce que les positions exactes de ces bornes fluctuent lorsque la même expérience / mesure est reproduite ; c'est-à-dire quand la même valeur \(\theta_0\) du paramètre a généré les données. On voit alors qu'on ne peut espérer faire mieux que de contrôler la fréquence / probabilité avec laquelle la vraie valeur \(\theta_0\) sera contenue dans l'intervalle (on dit aussi « la probabilité avec laquelle l'intervalle recouvrira \(\theta_0\) »). Cette probabilité minimale que nous allons appeler le niveau de l'intervalle est choisie par compromis entre convention et considérations pratiques. Les conventions typiques, celles que demandent par exemple la plupart des journaux scientifiques, sont d'avoir des niveaux égaux à 0,95 ou 0,99. Un niveau de 0,95 signifie que notre intervalle ne contiendra pas la vraie valeur du paramètre dans au plus 5% des cas. En pratique tout dépend de la conséquence de ce type d'erreur, s'il est grave de ne pas recouvrir la vraie valeur, on pourra opter pour un niveau de 0,99 ou plus ; dans le cas contraire, on pourra réduire le niveau. Maintenant, qualitativement, la largeur d'un intervalle de confiance (à un niveau donné) permet à une personne lisant le résultat de votre analyse de se faire une idée pas trop subjective de la précision avec laquelle le ou les paramètres d'intérêt ont été estimés. Cela permet aussi de comparer des répliques d'une même expérience comme l'illustre le cas suivant :
- le laboratoire A a publié que le constante de temps d'intérêt est contenue dans l'intervalle [0,91;1,23] avec un niveau de 0,95 ;
- le laboratoire B a publié que la même constante de temps est contenue dans l'intervalle [1,25;1,31] avec un niveau de 0,95.
Clairement, pour que les deux laboratoires aient effectivement mesuré la même constante de temps, celle-ci doit être hors de chacun des deux intervalles. La probabilité pour que cela ait lieu est inférieur ou égale à 0,05 dans chacun des deux cas. Comme on peut raisonnablement supposer que les deux expériences ont été effectuées indépendemment (au sens probabiliste / statistique du terme), la probabilité d'avoir \(\theta_0\) hors du premier intervalle et hors du second est le produit des probabilités de ces deux événements pris individuellement, c'est-à-dire qu'elle est inférieure ou égale à 0,05 x 0,05 = 0,0025. On peut douter que les deux labos ont effectivement mesuré la même chose…
4.6.1 Définitions
De façon un peu formelle, suivant le bouquin de Lejeune (p 136-137), on définit :
Définition Soit \(X_1,X_2,\ldots,X_n\) un échantillon issu d'une densité (ou fonction de masse) \(f(x;\theta_0)\) où \(\theta_0 \in \Theta\) est un paramètre inconnu de dimension 1. On appelle procédure d'intervalle de confiance de niveau \(\alpha\) tout couple de statistiques5 \((T_1,T_2)\) tel que, quelque soit \(\theta_0 \in \Theta\), on ait : \[\mathrm{Prob}_{\theta_0}\left(T_1 \le \theta_0 \le T_2\right) \ge \alpha \, .\]
Définition Dans le contexte de la définition précédente, soit \(x_1,x_2,\ldots,x_n\) une réalisation de \(X_1,X_2,\ldots,X_n\) conduisant à la réalisation \((t_1,t_2)\) de \((T_1,T_2)\). Alors l'intervalle \([t_1,t_2]\) est appelé intervalle de confiance de niveau \(\alpha\) pour \(\theta_0\) et l'on note : \[IC_{\alpha}(\theta_0) = [t_1,t_2] \, .\]
Remarque L'intervalle de confiance n'est rien d'autre que l'application numérique de la procédure suite à la réalisation de l'échantillon.
4.6.2 Construction
4.6.2.1 Méthode de Wald
Nos théorèmes sur la normalité asymptotique de l'EMV nous disent que, si les hypothèses de régularité sont vérifiées : \[\sqrt{n}\left(\hat{\theta}_n - \theta_0\right) \stackrel{L}{\rightarrow} \mathcal{N}\left(0,1/I(\theta_0) \right)\] où \[I(\theta_0) = \mathrm{Var}_{\theta_0}\left[l'(X_i;\theta_0)\right] \text{ et } l'(X_i;\theta) = \frac{\partial \log f(X_i;\theta)}{\partial \theta} \, .\] Dès lors que \(\hat{\theta}_n \stackrel{P}{\rightarrow} \theta_0\), on a aussi : \[\sqrt{n}\left(\hat{\theta}_n - \theta_0\right) \stackrel{L}{\rightarrow} \mathcal{N}\left(0,1/I(\hat{\theta}_n) \right)\] qui elle est directement utilisable en pratique. Notons : \[\widehat{es}_n \doteq \sqrt{\frac{1}{n I(\hat{\theta}_n)}} \, ,\] où « es » est un abréviation pour « erreur standard ». Si nous nous souvenons de notre définition des quantiles (ou percentiles) de la loi normale : \[ z_{\alpha} \doteq \Phi^{-1}(1-\alpha) \, , \] où \(\Phi\) désigne la fonction de répartition d'une variable aléatoire normale centrée, réduite (que nous désignons de façon générique par \(Z\)) et \(\Phi^{-1}\) désigne son inverse. On démontre :
Théorème Soit \[C_{\alpha} = \left[\hat{\theta}_n - z_{\alpha/2} \widehat{es}_n , \hat{\theta}_n + z_{\alpha/2} \widehat{es}_n \right] \, ;\] alors \(\mathrm{Prob}(\theta_0 \in C_{\alpha}) \rightarrow 1-\alpha\) quand \(n \rightarrow \infty\).
Preuve \[\begin{array}{l l l} \mathrm{Prob}(\theta_0 \in C_{\alpha}) & = & \mathrm{Prob}\left(\hat{\theta}_n - z_{\alpha/2} \widehat{es}_n \le \theta_0 \le \hat{\theta}_n + z_{\alpha/2} \widehat{es}_n \right) \\ & = & \mathrm{Prob}\left(- z_{\alpha/2} \le \frac{\theta_0-\hat{\theta}_n}{\widehat{es} _n} \le z_{\alpha/2} \right) \\ & \rightarrow & \mathrm{Prob}\left(- z_{\alpha/2} \le Z \le z_{\alpha/2} \right) = 1 - \alpha \end{array}\]
Remarque Pour \(\alpha=0,05\) on a \(z_{\alpha/2} = 1,96 \approx 2\), d'où la « règle » habituelle : \[\hat{\theta}_n \pm 2 \widehat{es}_n \] pour obtenir un intervalle de confiance de niveau (asymptotiquement) 0,95.
4.6.2.2 Méthode du rapport de vraisemblance
Comme d'habitude nous considérons l'échantillon \(X_1,X_2,\ldots,X_n\) de v.a. IID issues d'une densité (ou fonction de masse) \(f(x;\theta_0)\) où \(\theta_0 \in \Theta\).
Définition Nous notons \(\hat{\theta}_n\) l'EMV pour \(\theta_0\). La statistique du rapport de vraisemblance est alors définie par : \[\Lambda_n = \prod_{i=1}^n \frac{f(X_i;\hat{\theta}_n)}{f(X_i;\theta_0)} \, .\]
Théorème Sous les conditions de régularité qui garantissent la convergence et la normalité asymptotique de l'EMV (lorsque \(I(\theta) = J(\theta)\)), nous avons : \[2 \log \Lambda_n \stackrel{L}{\rightarrow} \chi^2_1 \, ,\] où \(\chi^2_1\) est une variable aléatoire suivant une loi du khi-deux à un degré de liberté.
Preuve Assez directe quand on a déjà établi la normalité asymptotique de l'EMV. Pour les détails, voir le bouquin de Knight (p 374-375) ou celui de Serfling (p 153).
Comment l'utiliser ? Notons \(k_{\alpha}\) le $1-α$-ième percentile (\(\alpha \in [0,1]\)) de la loi \(\chi^2_1\), et notons \(\mathcal{l}_n(\theta) = \sum_{i=1}^n \log f(X_i;\theta)\) ; nous avons alors par définition : \[\mathrm{Prob}\left(2 \left(l_n(\hat{\theta}_n) - l_n(\theta_0) \right) \le k_{\alpha}\right) \stackrel{L}{\rightarrow} 1 - \alpha \, .\] \(\hat{\theta}_n\) est défini comme la valeur de \(\theta\) à laquelle \(l_n(\theta)\) atteint son maximum, donc, localement au moins, lorsque \(\theta\) diminue à partir de \(\hat{\theta}_n\), \(l_n(\theta)\) doit diminuer de façon monotone ; de même quand \(\theta\) augmente à partir de \(\hat{\theta}_n\). Dans un voisinage \((\hat{\theta}_n-\delta_g,\hat{\theta}_n]\), \(l_n(\theta)\) doit donc devenir inversible ; notons \(l_{n,g}^{-1}\) cette fonction inverse. De même, dans un voisinage \([\hat{\theta}_n,\hat{\theta}_n+\delta_d)\), \(l_n(\theta)\) doit devenir inversible ; notons \(l_{n,d}^{-1}\) cette fonction inverse. Alors, l'événement \(2 \left(l_n(\hat{\theta}_n) - l_n(\theta_0) \right) \le k_{\alpha}\) qui est identique à \(l_n(\theta_0) \ge l_n(\hat{\theta}_n) - k_{\alpha}/2\) doit être identique (si \(k_{\alpha}/2\) n'est pas trop grand) à : \[l_{n,g}^{-1}\left(l_n(\hat{\theta}_n) - k_{\alpha}/2\right) \le \theta_0 \le l_{n,d}^{-1}\left(l_n(\hat{\theta}_n) - k_{\alpha}/2\right)\] et \[\mathrm{Prob}\left(l_{n,g}^{-1}\left(l_n(\hat{\theta}_n) - k_{\alpha}/2\right) \le \theta_0 \le l_{n,d}^{-1}\left(l_n(\hat{\theta}_n) - k_{\alpha}/2\right)\right) \stackrel{L}{\rightarrow} 1 - \alpha \, .\] Donc l'intervalle \[\left[ l_{n,g}^{-1}\left(l_n(\hat{\theta}_n) - k_{\alpha}/2\right), l_{n,d}^{-1}\left(l_n(\hat{\theta}_n)-k_{\alpha}/2\right)\right]\] est asymptotiquement \(IC_{\alpha}(\theta_0)\).
Vous vous demandez certainement pourquoi faut-il « s'embêter » à construire des intervalles de confiances par la méthode du rapport de vraisemblance (qui va clairement nécessiter, en général, deux inversions numériques de \(l_n\)) alors que la méthode de Wald, bien plus simple est disponible. L'exemple suivant devrait vous faire comprendre pourquoi.
4.7 Exemple : un compteur de photons à temps mort
Vous utilisez un compteur numérique de photons (à haute énergie). Votre compteur écrit les données qu'il collecte sur le disque de votre ordinateur. Les données sont les temps écoulés entre les arrivées successives de deux photons lorsque ceux-ci sont supérieurs à un « temps mort » \(\delta\). Si deux photons ou plus arrivent dans un intervalle de durée inférieure à \(\delta\), alors rien n'est enregistré. Vous êtes donc dans un contexte de données seuillées. Vous supposerez que la vraie distribution des intervalles entre temps d'arrivées est exponentielle, c'est-à-dire que la densité de probabilité pour que l'intervalle soit de durée \(t\) est : \[ p(t) = \nu \exp ( - t \nu)\; . \] Les données sont :
import scipy from scipy.stats import expon, uniform nu_vrai = 7./6. delta = 0.19 n_intervalles = 20 seed(20061001) itv = expon.ppf(uniform.rvs(loc=expon.cdf(delta,scale=1/nu_vrai),scale=1-expon.cdf(delta,scale=1/nu_vrai),size=n_intervalles),scale=1/nu_vrai) intervalles = np.round(itv,decimals=3) intervalles
array([ 1.138, 1.2 , 3.044, 3.026, 0.656, 2.574, 0.508, 0.704,
1.083, 0.836, 2.197, 0.228, 0.339, 5.402, 0.245, 1.166,
0.723, 3.045, 0.435, 1.119])
Les données ont été arrondies à la milliseconde la plus proche, mais nous ferons comme si elles avaient été enregistrées avec une précision arbitraire. La durée du temps mort \(\delta\) est de 0,19 s.
4.7.1 Expression analytique et valeur numérique de l'EMV
La densité exponentielle « complète » est \(p(t) = \nu \exp ( - t \nu)\), la fonction de répartition est donc \[ P(t) = 1 - \exp ( - t \nu) \] et \[ \textrm{Pr}\{T > \delta\} = \exp ( - \delta \nu) \; . \] La densité de probabilité supposée pour le problème est donc : \[ p(t \mid t \ge \delta) = \nu \exp \left( - (t-\delta) \nu\right)\; . \] La log vraisemblance du problème est ainsi : \[ l_n(\nu) = N \, \log \nu - \nu \sum_i (t_i-\delta) \; , \] où \(N=20\) et \(i=1,\ldots,20\). La fonction score (dérivée première) est : \[ l_n'(\nu) = N/\nu - \sum_i (t_i - \delta) \] et la dérivée seconde est \[ l_n''(\nu) = -N/\nu^2\; . \] Cette dernière est toujours négative (tant que \(N>0\), ce qui est le cas ici) et \(l_n'\) est donc concave et admet un maximum unique donné par : \[ \hat{\nu} = N / \sum_i (t_i - \delta) \; . \] Numériquement il vient :
nu_chapeau = 1/(mean(intervalles)-delta)
nu_chapeau
0.77315602288541818
4.7.2 Erreur type et intervalle de confiance à 95% avec la méthode de Wald
Le développement précédent nous donne : \[ \widehat{es}_{\hat{\nu}} = \hat{\nu} / \sqrt{N} \; , \] soit :
es_nu_chapeau = nu_chapeau/sqrt(n_intervalles)
es_nu_chapeau
0.17288294243851782
D'où l'intervalle de confiance à 95% avec la méthode de Wald :
np.round(nu_chapeau + 1.96*array([-1,1])*es_nu_chapeau,decimals=2)
array([ 0.43, 1.11])
4.7.3 Graphe comparant la fonction de log vraisemblance avec son approximation quadratique
Nous traçons le graphe de , \(l_n(\nu)\), pour \(\nu \in [-3*\sigma_{\hat{\nu}} + \hat{\nu},-3*\sigma_{\hat{\nu}} + \hat{\nu}]\). Nous y rajoutons celui de l'approximation quadratique que nous venons de faire (implicitement) pour obtenir votre intervalle de confiance : \(y = l_n(\hat{\nu}) - (\nu - \hat{\nu})^2/(2\, \widehat{es}_n^2)\).
def log_vrai(nu): return n_intervalles*((delta-mean(intervalles))*nu+log(nu)) nn = linspace(-3,3,101)*es_nu_chapeau + nu_chapeau plot(nn,[log_vrai(nu) for nu in nn],lw=2,color='black') xlabel('$\\nu$') ylabel('Log vraisemblance') y_max = log_vrai(nu_chapeau) y_min = min(log_vrai(nn[0]),log_vrai(nn[-1])) plot(nn,[y_max-(nu-nu_chapeau)**2/2/es_nu_chapeau**2 for nu in nn],lw=2,color='red') vlines(-1.96*es_nu_chapeau + nu_chapeau,y_min,y_max,color='black',linestyle='dashed') vlines(1.96*es_nu_chapeau + nu_chapeau,y_min,y_max,color='black',linestyle='dashed')
<matplotlib.collections.LineCollection object at 0x4b615d0>
savefig('img/coursIntroStats2014/comparaison-logvrai-et-quadratique-compteur-temps-mort.png') close() 'img/coursIntroStats2014/comparaison-logvrai-et-quadratique-compteur-temps-mort.png'
Figure 7 : La fonction de log vraisemblance (en noir) et son approximation quadratique (en rouge). En pointillés, les limites de l'intervalle de confiance à 95 % construit avec la méthode de Wald.
On voit que l'approximation quadratique commence à être « assez loin » de la log vraisemblance même dans le domaine défini par l'intervalle de confiance. Qualitativement, la convergence en loi de l'EMV vers une normale peut s'interpréter en disant que, si la taille de l'échantillon est suffisamment grande, le graphe de la log vraisemblance doit être très proche d'une parabole retournée. Le fait que le graphe ci-dessus s'éloigne « assez vite » de la parabole qui l'approche en son maximum, suggère que la taille de l'échantillon est trop petite pour que l'intervalle obtenu avec la méthode de Wald soit fiable.
4.7.4 Intervalle de confiance à 95% avec la méthode du rapport de vraisemblance
Numériquement, \(k_{0,05}\) vaut :
from scipy.stats import chi2 k_0p05 = chi2.ppf(1-0.05,1) k_0p05
3.8414588206941236
Nous allons donc chercher les abscisses des points d'intersection entre \(l_n(\nu)\) et une droite horizontale d'ordonnée \(l_n(\hat{\nu}) - k_{0,05}/2\). Pour trouver ces abscisses, nous devons trouver les racines de la fonction (de \(\nu\)) :
\[l_n(\hat{\nu}) - l_n(\nu) - k_{0,05}/2 \]
pour \(\nu \in [0,2;\hat{\nu}]\) d'une part et pour \(\nu \in [\hat{\nu};1,2]\) d'autre part. Nous allons faire cela avec la méthode de Brent mise en œuvre par la fonction brentq de scipy :
from scipy.optimize import brentq def cible(nu): return log_vrai(nu_chapeau) - log_vrai(nu) - k_0p05/2. IC_lr_g = brentq(cible,0.2,nu_chapeau) IC_lr_d = brentq(cible,nu_chapeau,1.2) [IC_lr_g,IC_lr_d]
[0.4818964626882697, 1.163206521355929]
plot(nn,[log_vrai(nu) for nu in nn],lw=2,color='black') xlabel('$\\nu$') ylabel('Log vraisemblance') hlines(log_vrai(nu_chapeau)-k_0p05/2.,0.2,1.4,color='red',lw=2) vlines(-1.96*es_nu_chapeau + nu_chapeau,y_min,y_max,color='black',linestyle='dashed') vlines(1.96*es_nu_chapeau + nu_chapeau,y_min,y_max,color='black',linestyle='dashed') vlines(IC_lr_g,y_min,y_max,color='red',linestyle='dashed') vlines(IC_lr_d,y_min,y_max,color='red',linestyle='dashed')
<matplotlib.collections.LineCollection object at 0x4c61ed0>
savefig('img/coursIntroStats2014/logvrai-et-logratio-compteur-temps-mort.png') close() 'img/coursIntroStats2014/logvrai-et-logratio-compteur-temps-mort.png'
Figure 8 : La fonction de log vraisemblance (en noir) et (en rouge) la ligne horizontale marquant le niveau « critique » du rapport de vraisemblance donnant (asymptotiquement) un niveau de 0,95. En pointillés noirs, les limites de l'intervalle de confiance à 95 % construit avec la méthode de Wald. En pointillés rouge, les limites de l'intervalle de confiance à 95 % construit avec la méthode du rapport de vraisemblance.
On voit que l'intervalle de la méthode du rapport de vraisemblance est « décalé » vers la droite par-rapport à l'intervalle obtenu avec l'approximation normale. Ceci est cohérent avec la différence entre l'approximation quadratique et la fonction de log vraisemblance.
4.7.5 Exercice
Vous prendrez la valeur de \(\hat{\nu}\) obtenue comme la vraie valeur. Vous simulerez de 500 à 1000 échantillons de taille 20 avec cette valeur. Pour chaque échantillon simulé, vous calculerez les \(IC_{0,95}\) avec la méthode de Wald et avec le méthode du rapport de vraisemblance. Vous obtiendrez ainsi les probabilités de recouvrement empiriques de vos intervalles. Conclusion ?
4.7.6 Solution
Pour ce type d'exercice ou d'étude basés sur la répétition d'une même analyse sur une collection de réplique, je vous recommande de commencer par définir de courtes fonctions qui effectuent une partie bien précise de l'analyse demandée. Ici, pour chaque réplique (échantillon de 20 observations simulées) nous allons construire un \(IC_{0,95}\) avec la méthode de Wald et un autre avec la méthode du rapport de vraisemblance. Il me semble donc raisonnable de commencer par définir deux fonctions, une qui, pour une réplique donnée, renvoie l'\(IC_{0,95}\) avec la méthode de Wald, l'autre qui renvoie l'\(IC_{0,95}\) obtenu avec la méthode du rapport de vraisemblance. La première des deux fonctions est simple à définir, il suffit de retrouver les quelques lignes de code utilisées ci-dessus pour calculer l'intervalle sur les données originales et de remplacer dans le code les données originales par l'argument de la fonction :
def IC_wald(data): nu_chapeau = 1/(mean(data)-delta) es_nu_chapeau = nu_chapeau/sqrt(n_intervalles) return [nu_chapeau - 1.96*es_nu_chapeau,nu_chapeau + 1.96*es_nu_chapeau]
Remarquez que la fonction retourne une liste dont les deux éléments sont les bornes de notre intervalle de confiance. Quand nous avions fait les calculs pas à pas sur les données originales, nous avions les bornes contenues dans un vecteur numpy. La liste, plus classique, choisie ici rend le traitement ultérieur un peu plus simple, c'est pourquoi elle a été choisie.
Quand on développe de courtes fonctions comme IC_wald, on a tout intérêt à effectuer de petits tests pour s'assurer qu'aucune erreur margeur n'a été commise. Ici, la première à faire est de vérifier que notre fonction nous redonne l'intervalle calculé précédemment « à la main » quand on l'applique aux mêmes données, les données originales :
IC_wald(intervalles)
[0.43430545570592327, 1.112006590064913]
Nous continuons en définissant une fonction qui calcule un \(IC_{0,95}\) par la méthode du rapport de vraisemblance. Ici, la tâche est un peu plus délicate car le calcul nécessite deux appels à brentq, appels pour lesquels une fonction cible doit être fournie. Cette fonction dépend des données et va donc devoir être redéfinie pour chaque nouveau jeu de données ; nous allons donc devoir la définir comme une fonction locale. Enfin, les bornes entre lesquelles la racine est cherchée doivent être fournies lors des deux appels à brentq. La borne droite, lors du premier appel (qui est la borne gauche lors du second est connue) est connue lors de l'appel puisqu'elle correspond à l'EMV. Le problème est le choix de la borne gauche (et celui de la borne droite lors du second appel). Nous avons précédemment résolu ce problème en examinant le graphe de la fonction, mais nous ne voulons pas utiliser cette approche ici puisque nous voulons une génération automatique de l'\(IC_{0,95}\). Une première stratégie consiste à prendre des bornes assez éloignées de l'EMV. En considérant que l'approximation quadratique n'est pas trop mauvaise, on se dit que fixer les bornes à un plus que 2 fois l'erreur type (\(\widehat{es}\)) ne devrait pas être trop mal. Dans un premier temps, j'avais décidé d'être « généreux » et j'avais fixer les bornes à \(5 \times \widehat{es}\) de part et d'autre de l'EMV. Là, les premiers essais m'ont générés des erreurs car le log d'un nombre négatif était demandé : en clair, l'EMV était « trop » proche de 0 et \(\widehat{es}\) était « trop » large ce qui donnait \(\hat{\nu} - 5 \times \widehat{es}\). J'ai donc décider de fixer la limite gauche lors du premier appel à brentq au maximum de \(\hat{\nu} - 5 \times \widehat{es}\) et d'un nombre suffisamment petit que j'ai fixé à 0,1. D'où la fonction :
def IC_rv(data): nu_chapeau = 1/(mean(data)-delta) def log_vrai(nu): return n_intervalles*((delta-mean(data))*nu+log(nu)) def cible(nu): return log_vrai(nu_chapeau) - log_vrai(nu) - k_0p05/2. es_nu_chapeau = nu_chapeau/sqrt(n_intervalles) IC_lr_g = brentq(cible,max(nu_chapeau-5*es_nu_chapeau,0.1),nu_chapeau) IC_lr_d = brentq(cible,nu_chapeau,nu_chapeau+5*es_nu_chapeau) return [IC_lr_g,IC_lr_d]
Là encore, nous vérifions qu'appliquée aux données originales, notre fonction nous redonne l'\(IC_{0,95}\) obtenue précédemment « à la main » :
IC_rv(intervalles)
[0.4818964626882665, 1.1632065213559313]
Nous pouvons alors effectuer notre série de simulations. Mais avant de nous lancer dans une simulation à taille réelle, il vaut mieux en faire une avec peu de répliques (disons 10) et vérifier que rien de franchement pathologique n'apparaît. Après seulement, on peut se lancer avec beaucoup de répliques. Ici j'ai en fait constaté que les calculs aller tellement vite que j'ai fini par faire 10000 répliques au lieu de 1000 :
wald = [] rv = [] nu_sim = 1/(mean(intervalles)-delta) for i in range(10000): echantillon = expon.ppf(uniform.rvs(loc=expon.cdf(delta,scale=1/nu_sim),scale=1-expon.cdf(delta,scale=1/nu_sim),size=n_intervalles),scale=1/nu_sim) echantillon = np.round(echantillon,decimals=3) wald.append(IC_wald(echantillon)) rv.append(IC_rv(echantillon))
Nous voulons maintenant, pour chacun des intervalles obtenus, tester si la vraie valeur (nu_sim) et, oui ou non, contenue dedans, puis compter combien de fois, elle l'est. Pour les intervalles calculés avec la méthode de Wald nous obtenons :
sum([ic[0] <= nu_sim <= ic[1] for ic in wald])
9538
Pour ceux calculés avec la méthode du rapport de vraisemblance nous avons :
sum([ic[0] <= nu_sim <= ic[1] for ic in rv])
9510
Dans ce cas, l'espérance du nombre de oui est 10000 x 0,95 = 9500 ; nous faisons donc un peu mieux avec la seconde méthode, mais la première ne donne pas des résultats catastrophiques.
4.7.7 Remarques
Cet exemple est clairement « un peu » artificiel (du point de vue méthodologique). En effet, comme l'EMV est une fonction de la moyenne empirique, nous aurions mieux fait de procéder comme dans la section 4.4.2. Nous aurions même pu décider de reparamétriser la loi des données en travaillant avec le temps caractéristique de l'exponentielle, plutôt que sa fréquence caractéristique.
5 Quelques exercices
5.1 Maximum de vraisemblance : structure de l'ADN
L'ADN des eukaryotes — groupe d'organismes dont nous faisons parti et dont les cellules contiennent un noyau — présente des structure à de nombreuses échelles différentes comme l'illustre la figure ci-dessous6 :
Les données que vous allez analyser portent sur la structure visible sur le quatrième panneau (en partant de la gauche) formée par les brins d'ADN de 30 nm de diamètre associés aux protéines de structure (scaffold protein). Les modèles utilisés pour décrire ces structures sont en fait simples voir très simples :
- les gens considèrent les boucles individuels – formées par le brin de 30 nm de diamètre entre deux contacts avec l'élément de structure, visibles sur le troisième panneau – comme des unités « homogènes » assimilables aux monomères d'un polymère linéaire ;
- la chaîne de monomères est modélisée comme une marche aléatoire à 3D (je sais, c'est un peu grossier comme hypothèse !), c'est-à-dire qu'on suppose que l'espace euclidien à 3D est équipé d'un réseau uniforme, que les monomères peuvent occuper les noeuds de ce réseau et que la chaîne est construite en ajoutant les monomères successifs au hasard parmi les 6 noeuds plus proches voisins, même s'ils sont déjà occupés ;
- la distance euclidienne entre deux éléments de la chaîne doit alors suivre une distribution gaussienne isotrope à 3D.
Expérimentalement, les gens peuvent marquer, avec des molécules fluorescentes, des séquences spécifiques de l'ADN d'un chromosome. Il est alors possible de tester expérimentalement le modèle simple « de marche aléatoire » de la façon suivante :
- deux morceaux d'un chromosome dont la séparation « linéaire » mesurée en millions de paires de bases (Mbp) est connue sont marqués ;
- une centaine de cellules, toutes marquées de façon identique et préparées dans les mêmes conditions, sont congelées très rapidement et « fixées » chimiquement ;
- la distance euclidienne entre les deux marques est mesurée dans le plan focal d'un microscope à fluorescence ;
- la projection dans le plan d'une gaussienne à 3D étant une gaussienne à 2D, la distance entre les marques doit suivre une loi de Rayleigh7 dont la densité est : \[f(r;θ) = \frac{r}{θ^2} \exp \left(\frac{-r^2}{2θ^2}\right)\, , \quad r \ge 0 \quad \mathrm{et} \quad θ > 0 \; ;\]
- il reste à ajuster le paramètre θ de la loi de Rayleigh aux données et à vérifier l'adéquation du modèle ajusté aux données.
Vous disposez de trois jeux de données obtenus sur le chromosome 4 (humain) et la figure ci-dessous, dans sa partie haute, vous permettra de visualiser les positions relatives des marqueurs8 :
- le fichier http://xtof.disque.math.cnrs.fr/data/CoursStat2013short.txt contient 96 mesures avec les marqueurs placés aux positions
C4-71etC4-15; c'est-à-dire avec une distance linéaire de 10 Mbp ; - le fichier http://xtof.disque.math.cnrs.fr/data/CoursStat2013medium.txt contient 249 mesures avec les marqueurs placés aux positions
E4etC4-46; c'est-à-dire avec une distance linéaire de 64 Mbp ; - le fichier http://xtof.disque.math.cnrs.fr/data/CoursStat2013long.txt contient 132 mesures avec les marqueurs placés aux positions
E4etC4-161; c'est-à-dire avec une distance linéaire de 192 Mbp.
Chaque fichier contient les distances mesurées en μm. Vous pourrez charger ces données dans votre espace de travail avec, par exemple :
from urllib2 import urlopen ## Si Python 3 utilisez la commande suivante a la place ce celle ci-dessus ## from urllib.request import urlopen u = urlopen("http://xtof.disque.math.cnrs.fr/data/CoursStat2013short.txt") petit = [float(x) for x in u.readlines()] u.close() u = urlopen("http://xtof.disque.math.cnrs.fr/data/CoursStat2013medium.txt") moyen = [float(x) for x in u.readlines()] u.close() u = urlopen("http://xtof.disque.math.cnrs.fr/data/CoursStat2013long.txt") grand = [float(x) for x in u.readlines()] u.close()
On vérifie alors que les listes générées ont au moins le bon nombre d'éléments :
[len(x) for x in [petit,moyen,grand]]
[96, 249, 132]
5.1.1 Questions
- Question 2.1 : vous écrirez la log-vraisemblance, la fonction score (dérivée de la log-vraisemblance par-rapport au paramètre) et l'information observée (opposée de la dérivée seconde de la log-vraisemblance par-rapport au paramètre) pour un échantillon de taille N, IID, suivant une loi de Rayleigh. Vous en déduirez l'expression analytique de l'estimateur du maximum de vraisemblance ;
- Question 2.2 : pour chacun des trois jeux de données vous trouverez l'estimateur du maximum de vraisemblance du paramètre θ de la loi de Rayleigh ainsi qu'un intervalle de confiance à 95% avec la méthode de Wald ;
- Question 2.3 : pour chacun des trois jeux de données vous construirez le graphe de la fonction de log-vraisemblance au voisinage de son maximum (sur un domaine de longueur comparable à celle de l'intervalle de confiance construit, par exemple, 3 fois l'erreur type) auquel vous superposerez l'approximation quadratique : \[y = l(\hat{θ}) - (\hat{θ} - θ)^2 / (2 \widehat{es}^2)\; ; \]
- Question 2.4 : vous obtiendrez un intervalle de confiance à 95% avec la méthode du rapport de vraisemblance pour chacun des trois jeux de données ;
- Question 2.5 : pour chacun des trois jeux de données vous construirez un histogramme des observations (en choisissant la largeur des classes par validation croisée) auquel vous superposerez la loi de Rayleigh ajustée. Le modèle ajusté vous semble-t-il satisfaisant ?
- Question 2.6 : pour chacun des trois jeux, vous construirez le graphe de la fonction de répartition empirique, dont le le code se trouve au début du cours, à laquelle vous rajouterez une bande de confiance à 95% (le code se trouve peu après celui définissant la construction du graphe de la fonction de répartition empirique) avant de rajouter la fonction de répartition ajustée ;
- Question 2.7 : vous construirez un graphe représentant votre paramètre estimé \(\hat{θ}\) en fonction de la racine carrée de la distance linéaire séparant les marqueurs. Qu'en concluez-vous sachant que l'écart type de la distance euclidienne entre l'origine et la fin d'une marche aléatoire croît comme la racine du nombre de pas quelle comporte ?
- Question 2.8 : pour un des jeux de données, vous étudierez la probabilité de recouvrement d'un intervalle de confiance à 95% obtenu avec la méthode de Wald par bootstrap paramétrique (comme nous l'avons fait dans l'exercice de la section 4.7.4).
Le module scipy.stats fournit une collection de méthodes qui vous permettent de calculer la densité, la fonction de répartition et de générer des nombres (pseudo-)aléatoires suivant une loi de Rayleigh.
5.1.2 Réponses
5.1.2.1 Question 2.1
Soient \(R_1,\ldots,R_N\) N variables aléatoires IID suivant une loi de Rayleigh de paramètre θ. La densité de probabilité conjointe s'écrit : \[p(R_1=r_1,\ldots,R_N=r_n) = \prod_{i=1}^N \frac{r_i}{θ^2} \, \exp\left(\frac{-r_i^2}{2\, θ^2}\right) \; .\] La log-vraisemblance s'écrit donc : \[\mathcal{l}(θ) = -2 N \log θ - \frac{1}{2\, θ^2} \sum_{i=1}^N r_i^2 \, ,\] où le terme \(\sum_{i=1}^N \log r_i\) a été éliminé puisqu'il ne dépend pas de θ. La fonction score est donc : \[S(θ) = -\frac{2 N}{θ} + \frac{1}{θ^3} \sum_{i=1}^N r_i^2 \] et l'information observée : \[\mathcal{J}(θ) = -\frac{2 N}{θ^2} + \frac{3}{θ^4} \sum_{i=1}^N r_i^2 \; .\] L'estimateur du maximum de vraisemblance (EMV), dans les bons cas au moins, est la (ou une des) racine(s) de la fonction score, ce qui nous donne ici : \[\hat{θ} = \sqrt{\frac{\sum_{i=1}^N r_i^2}{2 N}} \; .\] On voit de plus que : \[\mathcal{J}(\hat{θ}) = \frac{8 N^2}{\sum_{i=1}^N r_i^2} > 0\] on a donc bien un maximum puisque l'information observée est l'opposée de la dérivée seconde.
Utilisation de SymPy comme aide
Les suites ne sont pas encore mises en œuvre en tant que telles dans SymPy (dans la version stable, elles se trouvent dans la version en développement), nous ne pouvons donc par représenter un objet du type \(R_1,\ldots,R_n\), mais comme les données sont supposées IID, cela ne pose pas de gros problèmes, il faudra juste multiplier par \(n\) les scalaires et remplacer \(r\) par \(\sum_{i=1}^n r_i\) dans ce qui suit. Nous commençons donc avec :
import sympy as sy r, theta = sy.symbols('r,theta',real=True,positive=True) f = r*sy.exp(-r**2/2/theta**2)/theta**2
Puis nous obtenons la contribution d'une observation à la log vraisemblance :
sy.expand_log(sy.log(f))
-r**2/(2*theta**2) + log(r) - 2*log(theta)
La (contribution d'une observation à la) dérivée première de la log vraisemblance est :
sy.simplify(sy.diff(sy.log(f),theta))
r**2/theta**3 - 2/theta
La (contribution d'une observation à la) dérivée seconde de la log vraisemblance est :
sy.expand(sy.simplify(sy.diff(sy.log(f),theta,2)))
-3*r**2/theta**4 + 2/theta**2
On peut vérifier simplement que \(\mathrm{E}_{\theta}\left\{ \partial \log f(r;\theta) / \partial \theta \right\} = 0\) :
sy.integrate(sy.diff(sy.log(f),theta)*f,(r,0,sy.oo))
0
On trouve également directement l'expression de l'information de Fischer (\(\mathrm{E}_{\theta}\left\{\left(\partial \log f(r;\theta) / \partial \theta\right)^2\right\}\)) :
sy.integrate(sy.diff(sy.log(f),theta)**2*f,(r,0,sy.oo))
4/theta**2
Et on montre de même que \(\mathrm{E}_{\theta}\left\{\left( \partial \log f(r;\theta) / \partial \theta \right)^2\right\} = - \mathrm{E}_{\theta}\left\{\left( \partial^2 \log f(r;\theta) / \partial \theta^2 \right)^2\right\}\) :
-sy.integrate(sy.diff(sy.log(f),theta,2)*f,(r,0,sy.oo))
4/theta**2
5.1.2.2 Question 2.2
Il suffit d'écrire une fonction qui renvoie par exemple l'EMV, l'erreur type (racine carrée de l'inverse de l'information observée évaluée à l'EMV) et les bornes gauches et droites de l'intervalle de confiance. Nos données sont pour l'instant représentées en mémoire sous forme de liste or certains calculs de la fonction qui suit s'écrivent plus légèrement avec des array numpy, nous définissons donc la fonction comme acceptant une fonction d'un argument de type array et nous devrons donc convertir nos listes au moment de l'appel :
def tout_en_un_wald(distances): N = len(distances) r2 = sum(distances**2) theta_chapeau = sqrt(r2/2./N) es_chapeau = sqrt(r2/2)/2/N gauche = theta_chapeau - 1.96*es_chapeau droite = theta_chapeau + 1.96*es_chapeau return [theta_chapeau,es_chapeau,gauche,droite]
Telle que nous l'avons définie, la fonction tout_en_un_wald renvoie une liste à quatre éléments : l'EMV, l'erreur type, les limites gauche et droite de l'intervalle de confiance calculé avec la méthode de Wald.
Nous obtenons donc pour les trois jeux de données :
petit_res = tout_en_un_wald(array(petit)) moyen_res = tout_en_un_wald(array(moyen)) grand_res = tout_en_un_wald(array(grand)) [petit_res,moyen_res,grand_res]
[[1.1237775765989759, 0.057347534313519348, 1.0113764093444779, 1.2361787438534739], [2.0812132505770546, 0.065945765370177822, 1.9519595504515062, 2.2104669507026031], [3.31684629100925, 0.14434720687606015, 3.0339257655321723, 3.5997668164863277]]
5.1.2.3 Question 2.3
Le plus simple est de définir une fonction qui génère un graphe comme demandé pour un jeu de données passé comme paramètre (pour faciliter la lecture des graphes que nous allons juxtaposer horizontalement, je fais le graphe de \(l_n(\theta)-l_n(\hat{\theta})\)) :
def graphe_approx_quad(distances): distances = array(distances) stats = tout_en_un_wald(distances) N = len(distances) r2 = sum(distances**2) def lv(theta): return -2*N*log(theta) - r2/2./theta**2 tt = linspace(-stats[1]*3+stats[0],stats[1]*3+stats[0],401) plot(tt,lv(tt)-lv(stats[0]),color='black',lw=2) plot(tt,-(tt-stats[0])**2/stats[1]**2/2,color='red',linestyle='dashed',lw=2) xlabel("$\\theta$")
graphe_approx_quad
Et on obtient les figures avec :
subplot(131)
graphe_approx_quad(petit)
ylabel("$l_n(\\theta) - l_n(\hat{\\theta})$")
subplot(132)
graphe_approx_quad(moyen)
subplot(133)
graphe_approx_quad(grand)
savefig('img/coursIntroStats2014/Stat2013exam20130606F4.png') close() 'img/coursIntroStats2014/Stat2013exam20130606F4.png'
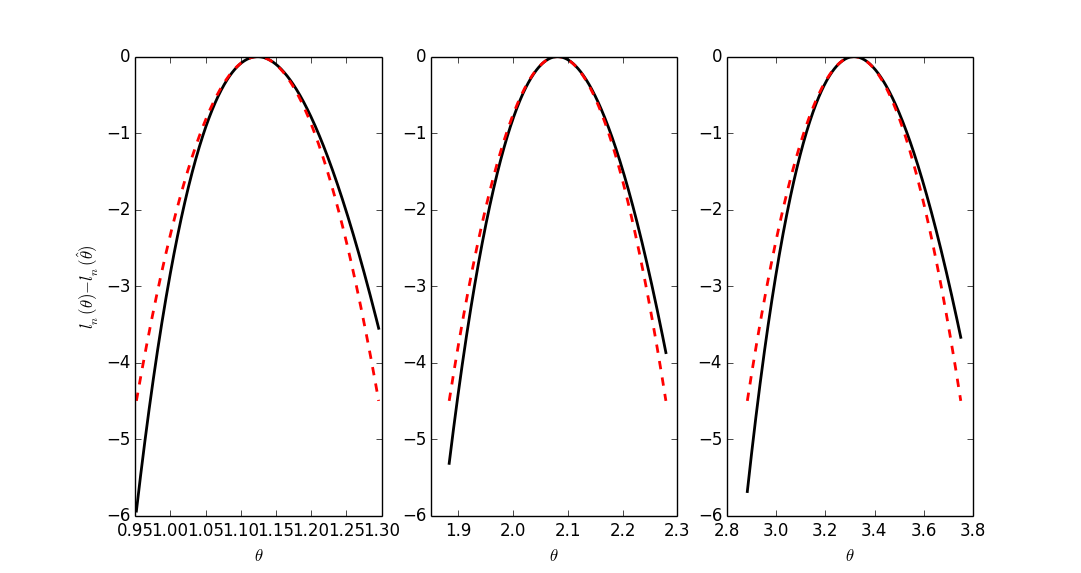
Figure 11 : Log-vraisemblances normalisées (\(l_n(\theta)-l_n{\hat{\theta}}\)) et approximations quadratiques pour les trois jeux de données : petit (gauche), moyen (milieu) et grand (droite).
On constate que nos fonctions de log-vraisemblance sont légèrement asymétriques et on s'attend donc à ce que nos intervalles basés sur la méthode de Wald soient légèrement faux.
5.1.2.4 Question 2.4
Pour obtenir les intervalles de confiance avec la méthode du rapport de vraisemblance, il suffit d'adapter la fonction IC_rv que nous avons définie précédemment :
from scipy.stats import chi2 from scipy.optimize import brentq k_0p05 = chi2.ppf(1-0.05,1) def tout_en_un_rv(distances): distances = array(distances) stats = tout_en_un_wald(distances) theta_chapeau = stats[0] N = len(distances) r2 = sum(distances**2) def log_vrai(theta): return -2*N*log(theta) - r2/2./theta**2 def cible(theta): return log_vrai(theta_chapeau) - log_vrai(theta) - k_0p05/2. es_theta_chapeau = stats[1] IC_lr_g = brentq(cible,max(theta_chapeau-6*es_theta_chapeau,0.1),theta_chapeau) IC_lr_d = brentq(cible,theta_chapeau,theta_chapeau+6*es_theta_chapeau) return [theta_chapeau,es_theta_chapeau,IC_lr_g,IC_lr_d]
Nous obtenons donc pour les trois jeux de données :
petit_res_rv = tout_en_un_rv(array(petit)) moyen_res_rv = tout_en_un_rv(array(moyen)) grand_res_rv = tout_en_un_rv(array(grand)) [petit_res_rv,moyen_res_rv,grand_res_rv]
[[1.1237775765989759, 0.057347534313519348, 1.020102594108281, 1.2462806227367074], [2.0812132505770546, 0.065945765370177822, 1.9583585222706963, 2.2174714041476324], [3.31684629100925, 0.14434720687606015, 3.052850354989577, 3.621204131468048]]
5.1.2.5 Question 2.5
Pour construite nos histogrammes en choisissant le nombre de classe par minimisation de l'erreur quadratique intégrée moyenne, nous suivons l'exercice de la section 3.3.3.1 et nous devons, si nous ne l'avons pas déjà fait, évaluer les définitions des fonctions fait_fre, j_chapeau, histogramme et histogramme_fct.
Pour le « petit » jeu de données nous avons alors :
mm_petit = arange(1,len(petit)) j_chapeau_petit = array([j_chapeau(array(petit),i) for i in mm_petit]) mm_petit[argmin(j_chapeau_petit)]
7
On construit le graphe de l'erreur quadratique intégrée moyenne en fonction du nombre de classes de l'histogramme ainsi que l'histogramme avec le nombre « optimal » de classe auquel on superpose la densité théorique (le module scipy.stats fourni une version de la densité de Rayleigh) :
cb_petit,f_chapeau_petit = histogramme(array(petit),mm_petit[argmin(j_chapeau_petit)]) subplot(121) plot(mm_petit,j_chapeau_petit,color="black",lw=2) grid() xlabel("Nombre de classes") ylabel(u"Erreur quadratique intégrée moyenne") subplot(122) plot(cb_petit[1:],f_chapeau_petit,ls='steps',color='black',lw=2) ylabel(u'Densité estimée') xlabel("Distance ($\\mu{}m$)") xx_petit = linspace(min(petit),max(petit),201) from scipy.stats import rayleigh plot(xx_petit, rayleigh.pdf(xx_petit,scale=petit_res[0]),color='red',lw=2)
savefig('img/coursIntroStats2014/Stat2013exam20130606F5.png') close() 'img/coursIntroStats2014/Stat2013exam20130606F5.png'
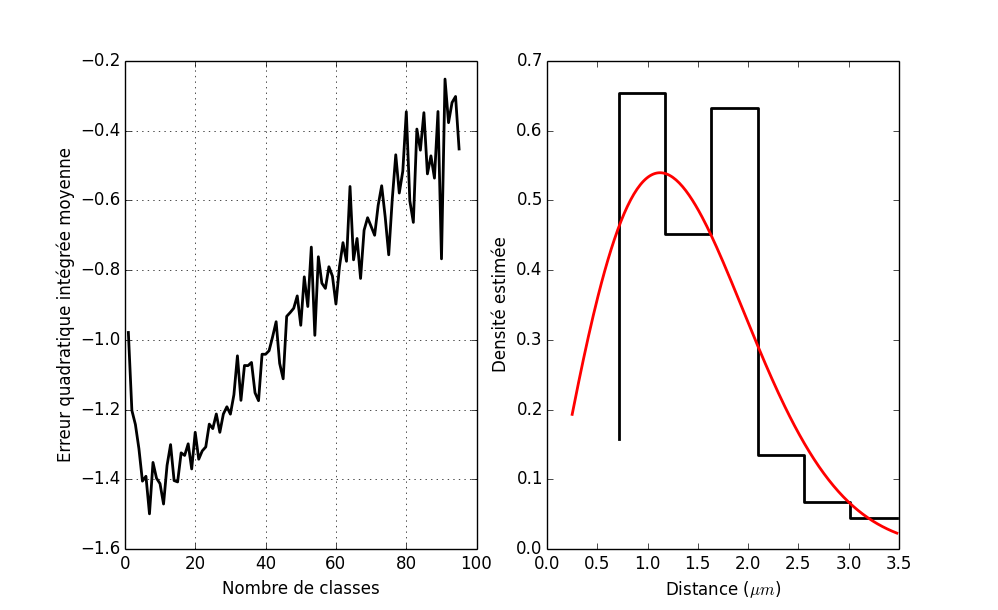
Figure 12 : Analyse de l'échantillon « petit ». À gauche, l'erreur quadratique intégrée moyenne en fonction du nombre de classes de l'histogramme. À droite, l'estimation de densité construite avec le nombre optimal de classe (noir) et la densité théorique superposée (rouge) après avoir fixé la valeur de son paramètre par la méthode du maximum de vraisemblance.
On constate que l'erreur quadratique intégrée moyenne ne varie pas trop entre 7 et 10 classes ; on pourrait aussi légitimement choisir de construire notre estimation de densité avec un peu plus de classes.
On répète cette séquence de commandes avec le jeu de données « moyen ».
mm_moyen = arange(1,len(moyen)) j_chapeau_moyen = array([j_chapeau(array(moyen),i) for i in mm_moyen]) mm_moyen[argmin(j_chapeau_moyen)]
6
cb_moyen,f_chapeau_moyen = histogramme(array(moyen),11) subplot(121) plot(mm_moyen,j_chapeau_moyen,color="black",lw=2) xlim([0,100]) grid() xlabel("Nombre de classes") ylabel(u"Erreur quadratique intégrée moyenne") subplot(122) plot(cb_moyen[1:],f_chapeau_moyen,ls='steps',color='black',lw=2) ylabel(u'Densité estimée') xlabel("Distance ($\\mu{}m$)") xx_moyen = linspace(min(moyen),max(moyen),201) plot(xx_moyen, rayleigh.pdf(xx_moyen,scale=moyen_res[0]),color='red',lw=2)
savefig('img/coursIntroStats2014/Stat2013exam20130606F6.png') close() 'img/coursIntroStats2014/Stat2013exam20130606F6.png'
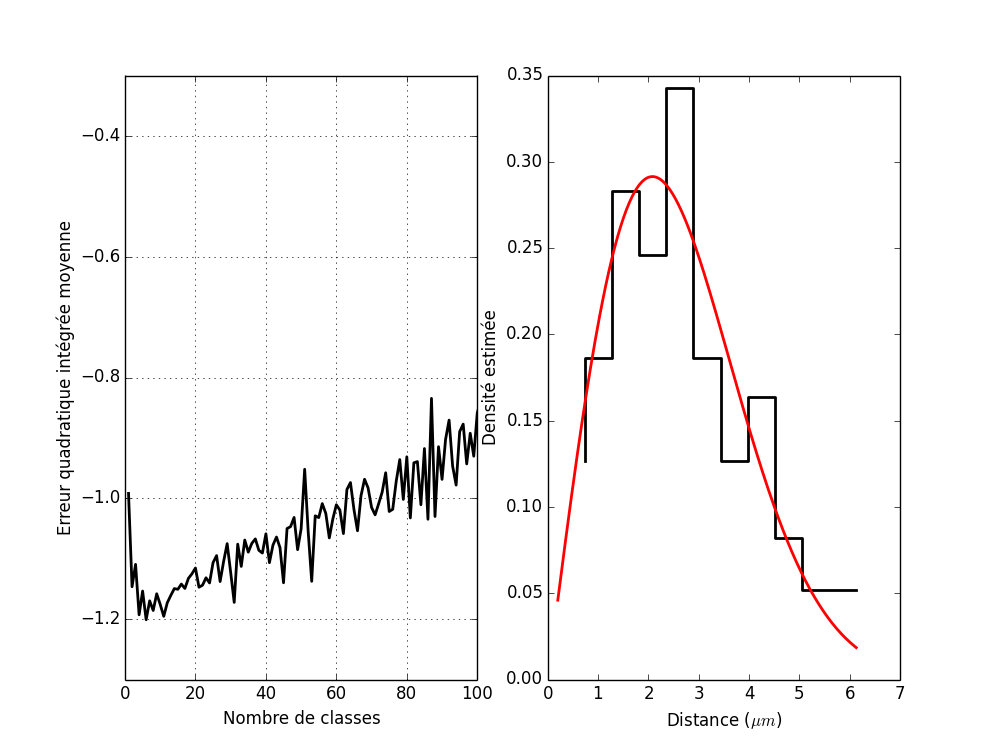
Figure 13 : Analyse de l'échantillon « moyen ». À gauche, l'erreur quadratique intégrée moyenne en fonction du nombre de classes de l'histogramme. À droite, l'estimation de densité construite avec le nombre presque optimal de classe (noir) — j'ai choisi d'utiliser 11 classes au lieu de 6 après avoir examiné le graphe de gauche — et la densité théorique superposée (rouge) après avoir fixé la valeur de son paramètre par la méthode du maximum de vraisemblance.
Puis avec le jeu de données « grand » :
mm_grand = arange(1,len(grand)) j_chapeau_grand = array([j_chapeau(array(grand),i) for i in mm_grand]) mm_grand[argmin(j_chapeau_grand)]
10
cb_grand,f_chapeau_grand = histogramme(array(grand),mm_grand[argmin(j_chapeau_grand)]) subplot(121) plot(mm_grand,j_chapeau_grand,color="black",lw=2) grid() xlabel("Nombre de classes") ylabel(u"Erreur quadratique intégrée moyenne") subplot(122) plot(cb_grand[1:],f_chapeau_grand,ls='steps',color='black',lw=2) ylabel(u'Densité estimée') xlabel("Distance ($\\mu{}m$)") xx_grand = linspace(min(grand),max(grand),201) plot(xx_grand, rayleigh.pdf(xx_grand,scale=grand_res[0]),color='red',lw=2)
savefig('img/coursIntroStats2014/Stat2013exam20130606F7.png') close() 'img/coursIntroStats2014/Stat2013exam20130606F7.png'
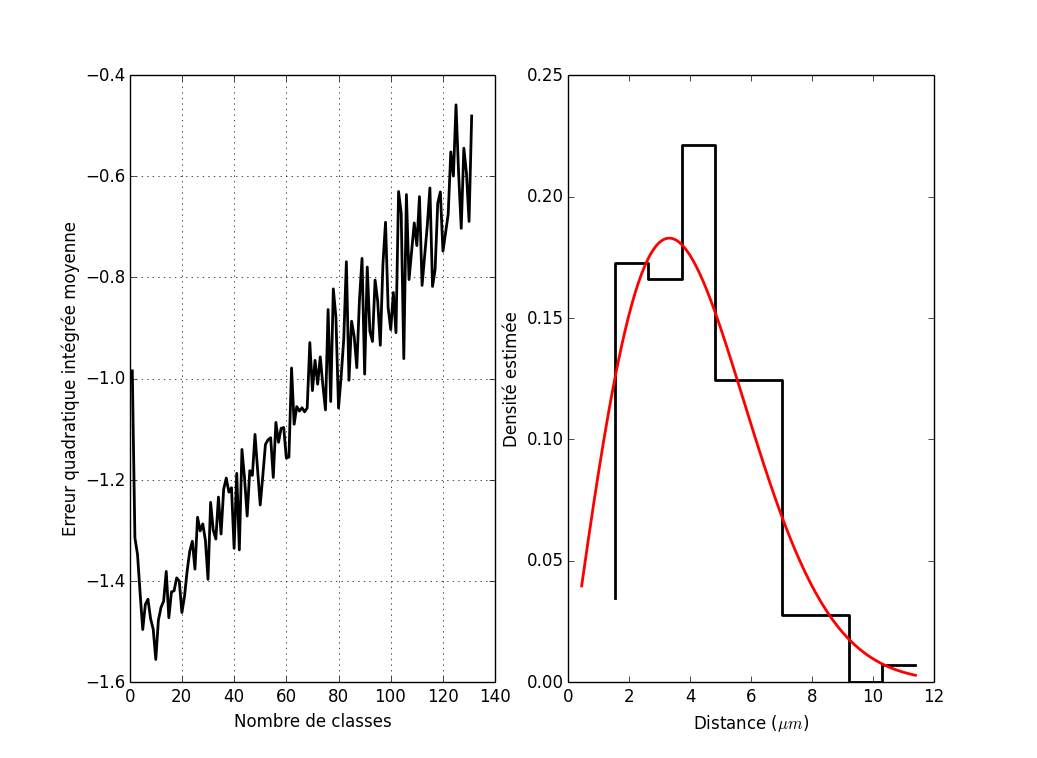
Figure 14 : Analyse de l'échantillon « grand ». À gauche, l'erreur quadratique intégrée moyenne en fonction du nombre de classes de l'histogramme. À droite, l'estimation de densité construite avec le nombre optimal de classe (noir) et la densité théorique superposée (rouge) après avoir fixé la valeur de son paramètre par la méthode du maximum de vraisemblance.
Conclusion Les ajustements sont compatibles avec les données (présentées sous forme d'histogramme en tout cas). On constate néanmoins que les histogrammes « tombent » à zéro vers la gauche (lorsqu'on s'approche de l'origine) plus vite que les densités estimées. Cela doit s'expliquer par le fait que les données viennent de mesures effectuées au microscope optique dont le pouvoir de résolution est limitée par la diffraction. De ce point de vue, si on examine les dix plus petites valeurs de chacun des trois échantillons, on pourrait être amené à penser que des objectifs différents ont été utilisés pour les données « petit » et « moyen » d'une part et « grand » d'autre part :
[sorted(donnees)[:10] for donnees in [petit,moyen,grand]]
[[0.25, 0.41, 0.43, 0.49, 0.5, 0.57, 0.58, 0.69, 0.73, 0.74], [0.2, 0.25, 0.25, 0.25, 0.25, 0.28, 0.37, 0.37, 0.43, 0.47], [0.44, 0.57, 0.79, 0.87, 1.01, 1.18, 1.54, 1.57, 1.62, 1.65]]
C'est une situation typique où une interaction directe entre le « statisticien », c'est-à-dire la personne qui fait l'analyse, et l'« expérimentateur » permet d'avancer plus vite. J'aurais personnellement tendance à utiliser plutôt un modèle à résolution limitée (proche de celui de notre compteur à temps mort) pour ce type de données. Mais avant de prendre ce genre de décision, il faut discuter avec les gens qui font les mesures et qui sont sensés connaître leurs instruments.
5.1.2.6 Question 2.6
La fonction de répartition est ici définie par :
\[F(r;\theta) = \int_{x=0}^r \frac{x}{\theta^2} \exp \left(-\frac{x^2}{\theta^2}\right) dx \]
d'où on déduit immédiatement que :
\[F(r;\theta) = 1-\exp \left(-\frac{r^2}{\theta^2}\right) \, .\]
Vous pouvez bien sûr utiliser SymPy pour trouver cette solution :
x = sy.symbols('x',real=True,positive=True) sy.integrate(f.subs(r,x),(x,0,r))
1 - exp(-r**2/(2*theta**2))
Mais si vous avez besoin de SymPy pour ça, vous avez un peu de soucis à vous faire…
Nous n'avons pas besoin de définir une fonction Python calculant la fonction de répartition d'une loi de Rayleigh puisque celle-ci est déjà définie dans scipy.stats. Donc, après avoir évaluer les définitions de plot_fre et de plot_fre_band, la réponse à la question est générée en quelques lignes :
subplot(1,3,1) plot_fre(petit) plot_fre_band(petit) ylabel(u"Fréquence") xlabel("Distance ($\\mu{}m$)") title("petit") plot(xx_petit,rayleigh.cdf(xx_petit,scale=petit_res[0]),color='red',lw=2) subplot(1,3,2) plot_fre(moyen) plot_fre_band(moyen) xlabel("Distance ($\\mu{}m$)") title("moyen") plot(xx_moyen,rayleigh.cdf(xx_moyen,scale=moyen_res[0]),color='red',lw=2) subplot(1,3,3) plot_fre(grand) plot_fre_band(grand) xlabel("Distance ($\\mu{}m$)") title("grand") plot(xx_grand,rayleigh.cdf(xx_grand,scale=grand_res[0]),color='red',lw=2)
savefig('img/coursIntroStats2014/Stat2013exam20130606F8.png') close() 'img/coursIntroStats2014/Stat2013exam20130606F8.png'
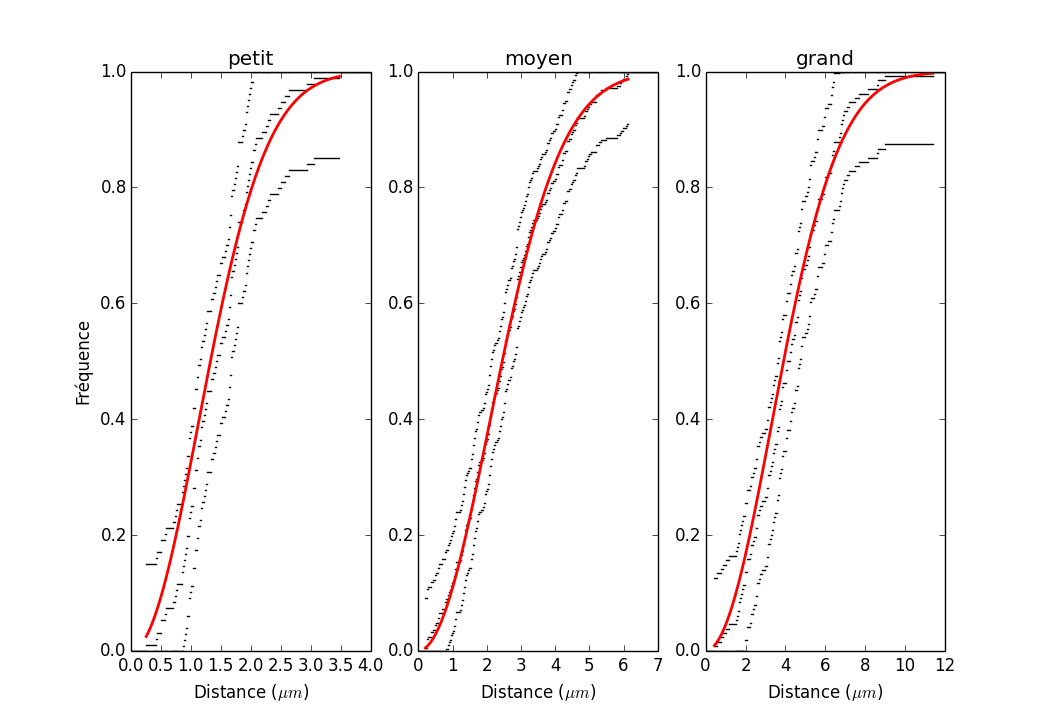
Figure 15 : Fonctions de répartition empiriques avec bande de confiance à 95% (noir) et fonction de répartition ajustées (rouge) pour les trois jeux de données.
Attention ! ici, les bandes de confiance ne constituent pas un test puisque la courbe théorique a été ajustée sur les mêmes données que celles utilisées pour construire les bandes. Néanmoins, comme nous n'avons ajusté qu'un seul paramètre et que la taille des jeux de données est de l'ordre de 100, on s'attend à ce que des bandes ayant une probabilité de 0,95 de contenir la vraie fonction de répartition soient très proches de celles représentées sur notre figure.
5.1.2.7 Question 2.7
Les distances entre marqueurs pour les trois jeux de données sont : 10, 64 et 194 Mbp, nos vecteurs de valeurs d'abscisse et d'ordonnée sont donc :
racine_distances = [sqrt(x) for x in [10,64,194]] theta_vecteur = [petit_res[0],moyen_res[0],grand_res[0]] plot(racine_distances,theta_vecteur,'ro') xlabel(u"Racine carrée de la distance entre marqueurs") ylabel(u"Paramètre estimé de la loi de Rayleigh ($\\mu{}m$)")
Text(50.625,0.5,u'Param\xe8tre estim\xe9 de la loi de Rayleigh ($\\mu{}m$)')
savefig('img/coursIntroStats2014/Stat2013exam20130606F9.png') close() 'img/coursIntroStats2014/Stat2013exam20130606F9.png'
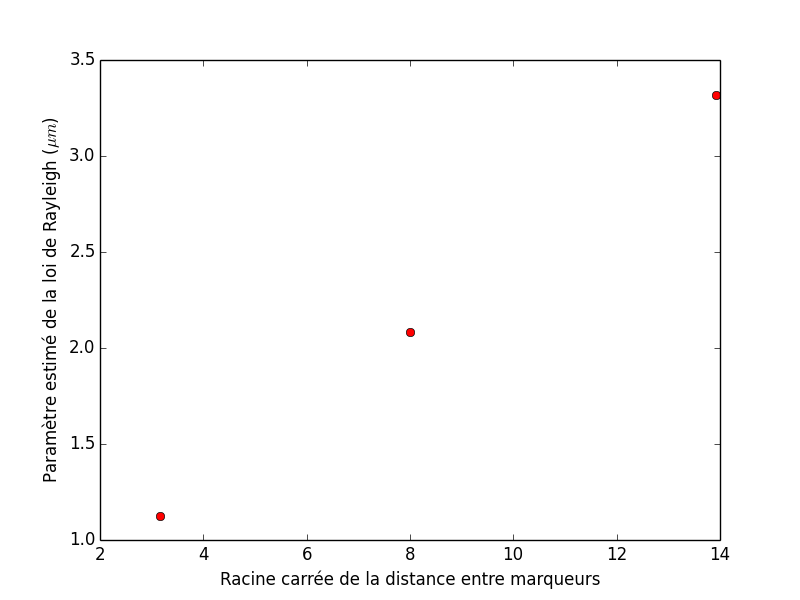
Figure 16 : Relation entre la racine carrée de la distance entre marqueurs (exprimée en Mbp) et le paramètre \(\theta\) de la loi de Rayleigh estimé par la méthode du maximum de vraisemblance.
Conclusion : nous n'avons que trois jeux de données, mais observer un tel accord entre théorie (très « naïve ») et vraies données expérimentales et assez rare ! (Nous sommes d'accord que la théorie prédit que les points devraient être alignés.)
5.1.2.8 Question 2.8
Nous allons considérer l'échantillon le plus défavorable du point de vue de l'inférence asymptotique, c'est-à-dire celui qui contient le moins d'observations. Il se trouve que c'est notre jeu de données « petit ». Nous allons en fait faire un peu plus que ce qui est demandé puisque nous allons sortir aussi nos EMV estimés ainsi que les logarithmes des rapports de vraisemblances (multipliés par 2) et les comparer à la loi normale asymptotique pour les premiers et à la loi du \(\chi^2_1\) pour les seconds. Nous calculons également des intervalles de confiance à 95% par la méthode du rapport de vraisemblance :
seed(20110928) wald = [] rv = [] theta_vrai = petit_res[0] taille = len(petit) from scipy.stats import chi2 k_0p05 = chi2.ppf(1-0.05,1) deux_N_log_theta_vrai = 2*taille*log(theta_vrai) theta_vrai_carre = theta_vrai**2 for i in range(10000): echantillon = rayleigh.rvs(scale=theta_vrai,size=taille) estimation_wald = tout_en_un_wald(echantillon) wald.append(estimation_wald) r2 = sum(echantillon**2) theta_chapeau = estimation_wald[0] es_theta_chapeau = estimation_wald[1] def log_vrai(theta): return -2*taille*log(theta) - r2/2./theta**2 def cible(theta): return log_vrai(theta_chapeau) - log_vrai(theta) - k_0p05/2. IC_lr_g = brentq(cible,max(theta_chapeau-6*es_theta_chapeau,0.1),theta_chapeau) IC_lr_d = brentq(cible,theta_chapeau,theta_chapeau+6*es_theta_chapeau) rapport = 2*(log_vrai(theta_chapeau) + deux_N_log_theta_vrai + r2/2./theta_vrai_carre) rv.append([rapport,IC_lr_g,IC_lr_d])
On vérifie alors que la loi normale asymptotique de l'EMV est bien atteinte (la variance de la loi normale doit alors être l'inverse de l'information de Fischer divisée par la taille de l'échantillon) :
subplot(121) plot_fre_band([x[0] for x in wald],0.99) xlabel("$\hat{\\theta}$") ylabel(u"Fréquence") xlim([0.9,1.4]) from scipy.stats import norm ww = linspace(0.9,1.4,201) plot(ww,norm.cdf(ww,loc=theta_vrai,scale=sqrt(theta_vrai**2/4/taille)),color='red') subplot(122) plot_fre_band([x[0] for x in rv],0.99) xlim([0,6]) xlabel("$2(\log \hat{\\theta} - \log \\theta_0)$") chichi = linspace(0,6,201) plot(chichi,chi2.cdf(chichi,1),color='red')
savefig('img/coursIntroStats2014/Stat2013exam20130606F10.png') close() 'img/coursIntroStats2014/Stat2013exam20130606F10.png'
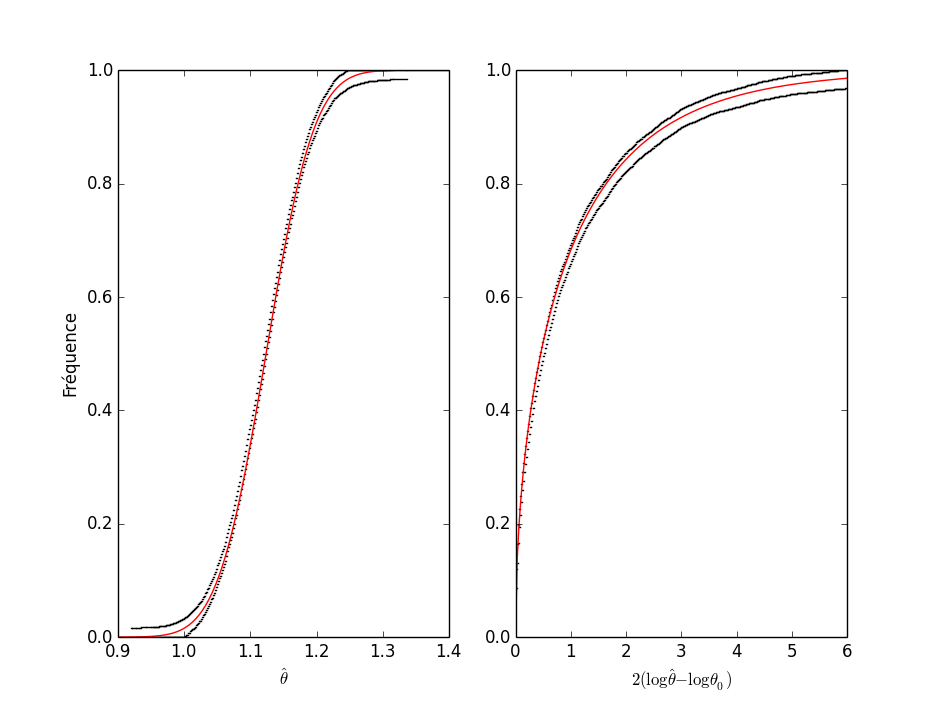
Figure 17 : À gauche : bande de confiance à 99% (noir) pour l'EMV du paramètre d'une loi de Rayleigh — lorsque la vraie valeur de celui-ci est round(theta_vrai,3) 1.124 et que la taille d'échantillon est taille 96 — et fonction de répartition pour la loi normale asymptotique (rouge). À droite : bande de confiance à 99% (noir) pour le double du log du rapport de vraisemblance et fonction de répartition pour la loi du \(\chi^2_1\) asymptotique (rouge).
La courbe théorique pour l'EMV (à gauche) sort très légèrement de la bande de confiance. C'est probablement dû à un léger biais de l'EMV (la courbe rouge se trouve plutôt du côté droit de la bande).
Le nombre d'intervalles de confiance obtenus avec la méthode de Wald qui contiennent effectivement la vraie valeur du paramètre est quand à lui :
sum([x[2] <= theta_vrai <= x[3] for x in wald])
9445
Cette valeur est un peu faible, comme le montre :
from scipy.stats import binom binom.cdf(sum([x[2] <= theta_vrai <= x[3] for x in wald]),len(wald),0.95)
0.0068274635784784455
Par contre avec le rapport de vraisemblance nous obtenons respectivement :
sum([x[1] <= theta_vrai <= x[2] for x in rv])
9469
et :
binom.cdf(sum([x[1] <= theta_vrai <= x[2] for x in rv]),len(rv),0.95)
0.08179457147689824
Nous devrions donc plutôt utiliser des intervalles calculés par la méthode du rapport de vraisemblance et, peut être, corriger le biais (mais je ne vous ai pas expliqué comment le faire).
5.2 Examen du 12 juin 2014
L'énoncer et le corrigé de l'examen sont disponibles. Pour les curieux, le fichier source est aussi disponible.
Notes de bas de page:
Nous avons supposé ici que toutes les réalisations sont différentes (\(x_i \neq x_j\) pour \(i \neq j\)) ; si tel n'est pas le cas, on aura moins d'éléments dans la version ordonnée et la hauteur des sauts sera égale à la multiplicité des valeurs correspondantes dans l'échantillon de départ.
Robert J. Serfling (1980) Approximation Theorems of Mathematical Statistics. Wiley.
Barnett, V. D. (1966) Evaluation of the Maximum-Likelihood Estimator where the Likelihood Equation has Multiple Roots. Biometrika 53, 151-165.
L'EMV est « optimal » lorsque la densité (ou fonction de masse) \(f_0\) qui a généré les données fait partie de la famille de modèles considérée (\(f_0 \in \mathcal{F}\) ou \(f_0(x) = f(x;\theta_0)\) avec \(\theta_0 \in \Theta\)) dans la mesure où \(\hat{\theta}_n \stackrel{P}{\rightarrow} \theta_0\) et où la variance de l'estimateur est (asymptotiquement) minimale.
Une statistique est une fonction définie sur l'espace des échantillons (lui même, dans le cas IID, produit cartésien de l'espace des épreuves associé à un \(X_i\)) ; c'est donc une variable aléatoire (on suppose la fonction mesurable).
Prenez une loi gaussienne istrope à 2D et passez en coordonnées polaires : http://fr.wikipedia.org/wiki/Loi_de_Rayleigh.
Figure 1 de Yokota et col. (1995) Evidence for the organization of chromatin in megabase pair-sized loops arranged along a random walk path in the human G0/G1 interphase nucleus. The Journal of Cell Biology 130(6), 1239-1249.