Cours d'introduction à la statistique et à l'analyse de données : Notes de cours
Table des matières
- 1. Introduction
- 2. Prise en main de
R- 2.1. Notes sur la régression linéaire par la méthode des moindres carrés
- 2.2. Un exemple de régression linéaire par la méthode des moindres carrés
- 2.2.1. Téléchargement des données
- 2.2.2. Analyse avec
R- 2.2.2.1. Matrice \(\mathbf{X}\) du plan d'expérience
- 2.2.2.2. Décomposition QR
- 2.2.2.3. Estimateur des moindres carrés
- 2.2.2.4. Tests d'adéquation
- 2.2.2.5. Critique et modification du modèle initial
- 2.2.2.6. Intervalles de confiance des paramètres
- 2.2.2.7. Faire tout cela en une seule ligne de commande de
R - 2.2.2.8. Pourquoi s'embêter à homogénéiser la variance ?
- 2.2.3. Analyse avec
GNU octave - 2.2.4. Analyse en
Common Lisp
- 3. L'estimation par « maximum de vraisemblance »
- 3.1. La fonction de vraisemblance
- 3.2. La fonction de log-vraisemblance
- 3.3. L'estimateur du maximum de vraisemblance
- 3.4. Fonctions associées à la fonction de log-vraisemblance
- 3.5. Ce que dit la théorie
- 3.6. Premier exemple simple
- 3.7. Un deuxième exemple à peine plus compliqué
- 3.8. Retour sur les données de fertilité de la communauté Hutterite considérées par Ihaka
- 4. Quelques exercices
- 4.1. Une épidémie de rougeole : le sujet d'examen de juin 2011
- 4.1.1. Question 1
- 4.1.2. Réponse 1
- 4.1.3. Question 2
- 4.1.4. Réponse 2
- 4.1.5. Complément 2
- 4.1.6. Question 3
- 4.1.7. Réponse 3
- 4.1.8. Question 4
- 4.1.9. Réponse 4
- 4.1.10. Complément 4
- 4.1.11. Question 5
- 4.1.12. Réponse 5
- 4.1.13. Complément 5
- 4.1.14. Question 6
- 4.1.15. Réponse 6
- 4.1.16. Question 7
- 4.1.17. Réponse 7
- 4.1.18. Question 8
- 4.1.19. Réponse 8
- 4.1.20. Question 9
- 4.1.21. Réponse 9
- 4.1.22. Question 10
- 4.1.23. Réponse 10
- 4.1.24. Question 11
- 4.1.25. Réponse 11
- 4.2. Un compteur de photons à temps mort
- 4.3. Données censurées ou tronquées
- 4.1. Une épidémie de rougeole : le sujet d'examen de juin 2011
- 5. Examen du 6 juin 2013
(defadvice org-mode-flyspell-verify (after my-org-mode-flyspell-verify activate) "Don't spell check src blocks." (setq ad-return-value (and ad-return-value (not (org-in-src-block-p)) (not (member 'org-block-begin-line (text-properties-at (point)))) (not (member 'org-block-end-line (text-properties-at (point))))))) (unless (find "xetex-fr" org-latex-classes :key 'car :test 'equal) (add-to-list 'org-latex-classes '("xetex-fr" "\\documentclass{scrartcl} \\usepackage{xunicode,fontspec,xltxtra} \\usepackage[frenchb]{babel} \\usepackage{graphicx,longtable,url,rotating} \\usepackage{minted} \\usepackage{unicode-math} \\newminted{common-lisp}{fontsize=\\footnotesize} \\frenchbsetup{og=«, fg=»} \\usepackage[xetex, colorlinks=true, urlcolor=blue, plainpages=false, pdfpagelabels, bookmarksnumbered]{hyperref} \\setromanfont[Mapping=tex-text]{Liberation Serif} \\setsansfont[Mapping=tex-text]{Liberation Sans} \\setmonofont[Mapping=tex-text]{Liberation Mono} \\setmathfont{Latin Modern Math} [NO-DEFAULT-PACKAGES] [EXTRA]" ("\\section{%s}" . "\\section*{%s}") ("\\subsection{%s}" . "\\subsection*{%s}") ("\\subsubsection{%s}" . "\\subsubsection*{%s}") ("\\paragraph{%s}" . "\\paragraph*{%s}") ("\\subparagraph{%s}" . "\\subparagraph*{%s}")))) (add-to-list 'org-latex-minted-langs '(R "r")) (setq org-latex-minted-options '(("bgcolor" "shadecolor") ("fontsize" "\\scriptsize"))) (setq org-latex-pdf-process '("xelatex -shell-escape -interaction nonstopmode -output-directory %o %f" "xelatex -shell-escape -interaction nonstopmode -output-directory %o %f" "xelatex -shell-escape -interaction nonstopmode -output-directory %o %f")) (setq org-babel-export-evaluate nil)
1 Introduction
Le cours va être orienté vers des applications « réelles » (ou assez proche de celles-ci). Je ne passerai pas de temps à prouver les théorèmes que nous allons employer, mais après (ou avant) les avoir énoncés, j'emploierai des simulations les illustrant. Les bouquins indiqués en fin d'introduction contiennent les preuves. Je précise aussi que j'emploie la locution « analyse de données » dans l'intitulé du cours au sens « naïf » du terme, c'est-à-dire pas comme les statisticiens français qui entendent par là un ensemble de méthodes d'analyse exploratoire impliquant principalement l'analyse en composantes principales (ACP). Ici « analyse de données » correspond à la situation familière à toute personne ayant passé ne serait-ce qu'une journée dans un laboratoire expérimentale : une expérience a été effectuée, les données sont « bruitées », on souhaite estimer certains paramètres — décrivant les données ou propres au modèle théorique supposé sous-jacent — ainsi que quantifier la précision de cette évaluation.
Comme faire de la statistique dans un contexte « réaliste » implique, de nos jours au moins, de manipuler de grands vecteurs ou table de données, nous ne pouvons pas vraiment nous passer d'utiliser un logiciel ; c'est pourquoi nous allons employer relativement « intensivement » dans ce cours le logiciel R. C'est un logiciel open source, gratuit et disponible sur tous les systèmes d'exploitation que vous êtes susceptibles de rencontrer. Les débutants ne connaissant pas emacs auront intérêt à utiliser R avec l'interface graphique RStudio, ce que nous ferons dans le cours. Les utilisateurs de emacs pourront installer le paquet ESS (Emacs Speaks Statistics) et consulter les excellents didacticiels (en anglais) de Stephen Eglen. Les curieux qui voudraient se mettre à emacs peuvent commencer, après avoir pris le tour, avec Being Productive With Emacs de Phil Sung (encore en anglais). Les utilisateurs de MATLAB® pourront consulter MATLAB® / R Reference de David Hiebeler.
Quelques bouquins de référence :
- « Statistique : la théorie et ses applications » de Michel Lejeune chez Springer, excellent ;
- Mathematical Statistics and Data Analysis de John Rice, aussi excellent mais en anglais ;
- All of Statistics et All of Nonparametric Statistics de Larry Wasserman, très bonnes synthèses mais un peu secs pour les débutants ;
- Mathematical Statistics de Keith Knight, ma meilleure source pour les preuves des théorèmes ;
- « Le logiciel R » de Pierre Lafaye de Micheaux, Rémy Drouilhet et Benoît Liquet, chez Springer ; c'est pour moi le meilleur bouquin généraliste sur
R, même si je prends en compte les (très nombreux) bouquins en anglais.
2 Prise en main de R
options(OutDec=",")
.
Nous allons consacrer les deux ou trois premiers cours à une prise en main du logiciel R et, comme je suis paresseux, nous allons le faire en suivant le début du cours de Ross Ihaka — un des deux, avec Robert Gentleman, développeurs originaux de R — intitulé Statistical Computing (Graduate). Nous utiliserons en particulier :
- R basics ;
- Programming ;
- Matrices ;
- Numerics.
Rassurez-vous, cette prise en main de R est aussi l'occasion d'introduire pas mal de concepts clés en statistique.
2.1 Notes sur la régression linéaire par la méthode des moindres carrés
J'essaie ici « d'éclaircir » le contenu des dernières diapos (59-71) du troisième cours d'Ihaka (sur les matrices). (Je vais suivre le premier chapitre du bouquin de Douglas Bates et Donald Watts Nonlinear Regression Analysis and Its Applications publié chez John Wiley & Sons en 1988.) Nous allons ici utiliser un jeu de données du bouquin ; jeu de données qu'on trouvera dans le paquet NRAIA sur CRAN (the Comprehensive R Archive Network). Nous devrons donc probablement commencer par installer le paquet, avec la commande install.packages ou via les menus déroulants pour ceux qui utilisent Rstudio :
install.packages("NRAIA")
Lorsque vous utilisez install.packages pour la première fois dans une session, R va typiquement vous demander (par une fenêtre « pop-up ») quel miroir vous souhaitez utiliser ; en général, je choisis le miroir autrichien qui est proche du haut de la liste et qui est le dépôt central (donc à priori plus à jour, même si cela ne fait pas grande différence).
Une fois le paquet installé, nous le chargeons dans l'espace de travail avec la commande library :
library(NRAIA)
| NRAIA |
| lattice |
| stats |
| graphics |
| grDevices |
| utils |
| datasets |
| methods |
| base |
Nous allons maintenant pouvoir avoir accès aux données PCB avec :
data(PCB)
Ce jeu de données se présente sous forme d'un data.frame à 28 lignes et 2 colonnes. Il contient des mesures de concentrations de Polychlorobiphényle (PCB) dans des poissons capturés dans le lac Cayuga (Nord de l'état de New-York). Les poissons avaient marqués lors de leur seconde année de vie, ce qui permettait de déterminer leur âge au moment de la capture. Pour avoir plus de détails sur ce jeu de données, tapez :
?PCB
La première colonne de PCB contient l'âge du poisson (en année) et la seconde, la concentration de PCB exprimée en Partie par million (ppm).
On obtient un graphe en « nuage de points » des données avec :
par(cex=2) with(PCB,plot(age, conc, xlab="âge (année)",ylab="Concentration de PCB (ppm)"))
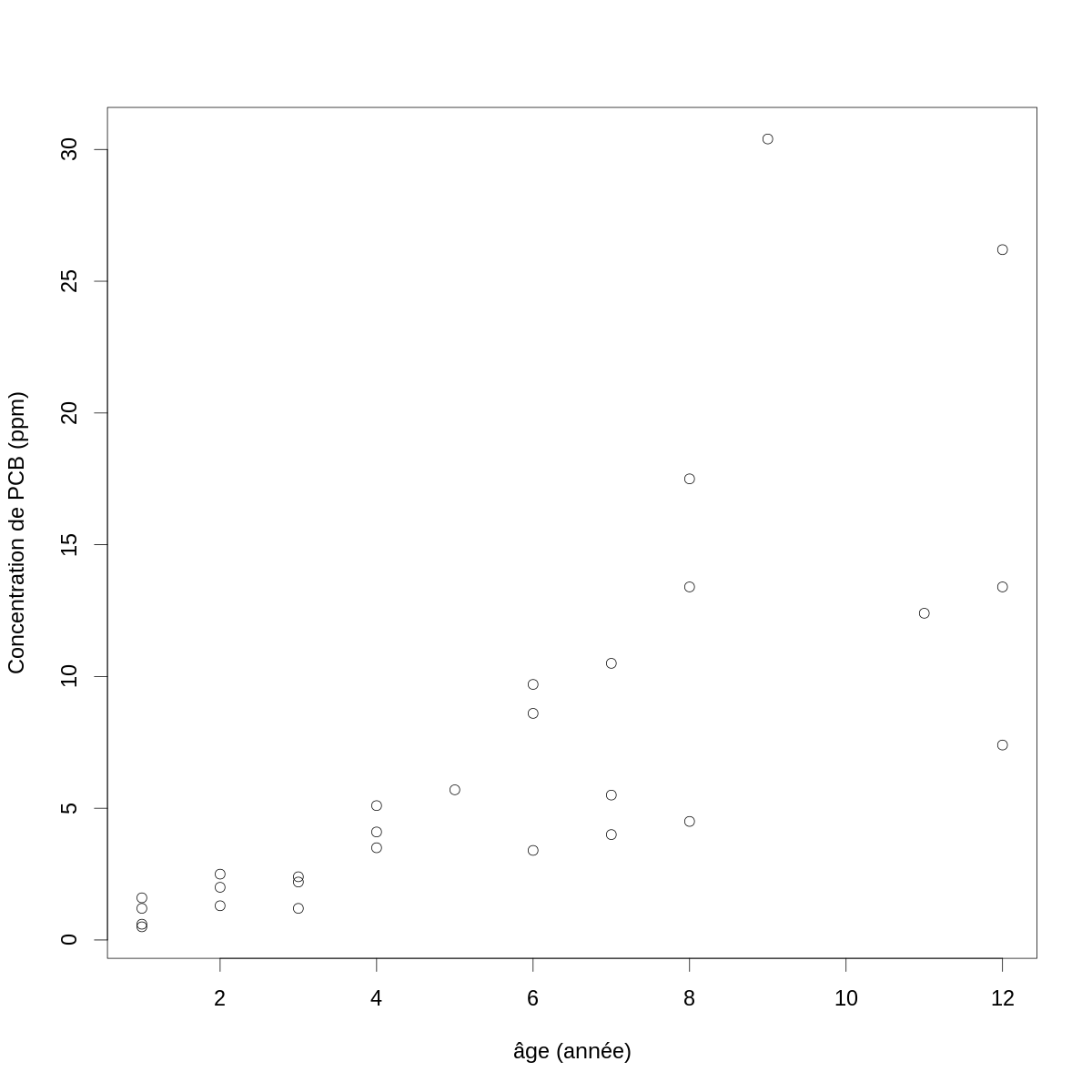
Figure 1 : Concentration de PCB en fonction de l'âge chez des poissons du lac Cayuga.
Lorsqu'on effectue une régression linéaire, on modélise une série d'observations d'une « variable expliquée » (ici les mesures de concentrations) comme une combinaison linéaire de « variables prédictives » (ici il n'y en a qu'une seule, l'âge du poisson). Concrètement, pour chacune des 28 mesures de concentration, \(conc_i\), nous allons supposer que : \[Y_i = f(conc_i) = β_0 + β_1 \, g(age_i) + Z_i \; ,\] où \(f\) et \(g\) sont des fonctions que nous pouvons choisir. Dans le cas le plus simple, nous les prendrons toutes deux égales à l'identité ; mais cela n'est clairement pas possible ici. \(β_0\) et \(β_1\) sont des paramètres à déterminer et \(Z_i\) est une variable aléatoire, elle décrit « le bruit ». On note typiquement \(\mathbf{Y}\) la variable expliquée et \(\mathbf{y}\) son observation. Ici \(\mathbf{y}\) est (en prenant l'identité pour \(f\)) :
options(OutDec=",") PCB$conc
[1] 0,6 1,6 0,5 1,2 2,0 1,3 2,5 2,2 2,4 1,2 3,5 4,1 5,1 5,7 3,4 [16] 9,7 8,6 4,0 5,5 10,5 17,5 13,4 4,5 30,4 12,4 13,4 26,2 7,4
La première commande ci-dessus, options(OutDec=","), me permet d'avoir une virgule à la place d'un point comme séparateur des parties entières et décimales dans les résultats affichés par R (labels des axes de figures compris) mais pas dans les commandes passées à l'interpréteur pour lequel le point reste la règle.
On note typiquement \(\mathbf{X}\) la matrice des variables explicatives, matrice dont la première colonne est constituée uniformément de 1 si on souhaite inclure dans le modèle une ordonnée à l'origine. Ici \(\mathbf{X}\) est (en prenant l'identité pour \(g\)) :
cbind(1,PCB$age)
| 1 | 1 |
| 1 | 1 |
| 1 | 1 |
| 1 | 1 |
| 1 | 2 |
| 1 | 2 |
| 1 | 2 |
| 1 | 3 |
| 1 | 3 |
| 1 | 3 |
| 1 | 4 |
| 1 | 4 |
| 1 | 4 |
| 1 | 5 |
| 1 | 6 |
| 1 | 6 |
| 1 | 6 |
| 1 | 7 |
| 1 | 7 |
| 1 | 7 |
| 1 | 8 |
| 1 | 8 |
| 1 | 8 |
| 1 | 9 |
| 1 | 11 |
| 1 | 12 |
| 1 | 12 |
| 1 | 12 |
Avec cette représentation, chaque ligne correspond à un individu. On emploie ainsi la notation matricielle suivante : \[\mathbf{Y} = \mathbf{X} \, \mathbf{β} + \mathbf{Z} \; ,\] où \(\mathbf{Y}\) est une variable aléatoire vectorielle à \(n\) éléments (le nombre d'observations), \(\mathbf{X}\) est une matrice \(n \times p\), \(\mathbf{β}\) est un vecteur à \(p\) éléments et \(\mathbf{Z}\) est une variable aléatoire vectorielle à \(n\) éléments que nous allons typiquement considérer comme IID de moyenne nulle et de variance finie σ2.
Le premier problème que nous devons résoudre, si nous voulons en rester à la régression linéaire, est trouver une fonction \(f\) qui nous atténue les « écarts aux hypothèses » clairement visibles sur la figure \ref{fig:conc-vs-age} : la variance augmente avec la concentration. Les fonctions \(f\) à tester dans ces cas là sont des fonctions racine, \(f(x)=x^{1/k}\), \(k > 1\) et la fonction log. Ici avec la fonction log donne :
par(cex=2) with(PCB,plot(age, conc, xlab="âge (année)",ylab="Concentration de PCB (ppm)",log="y"))
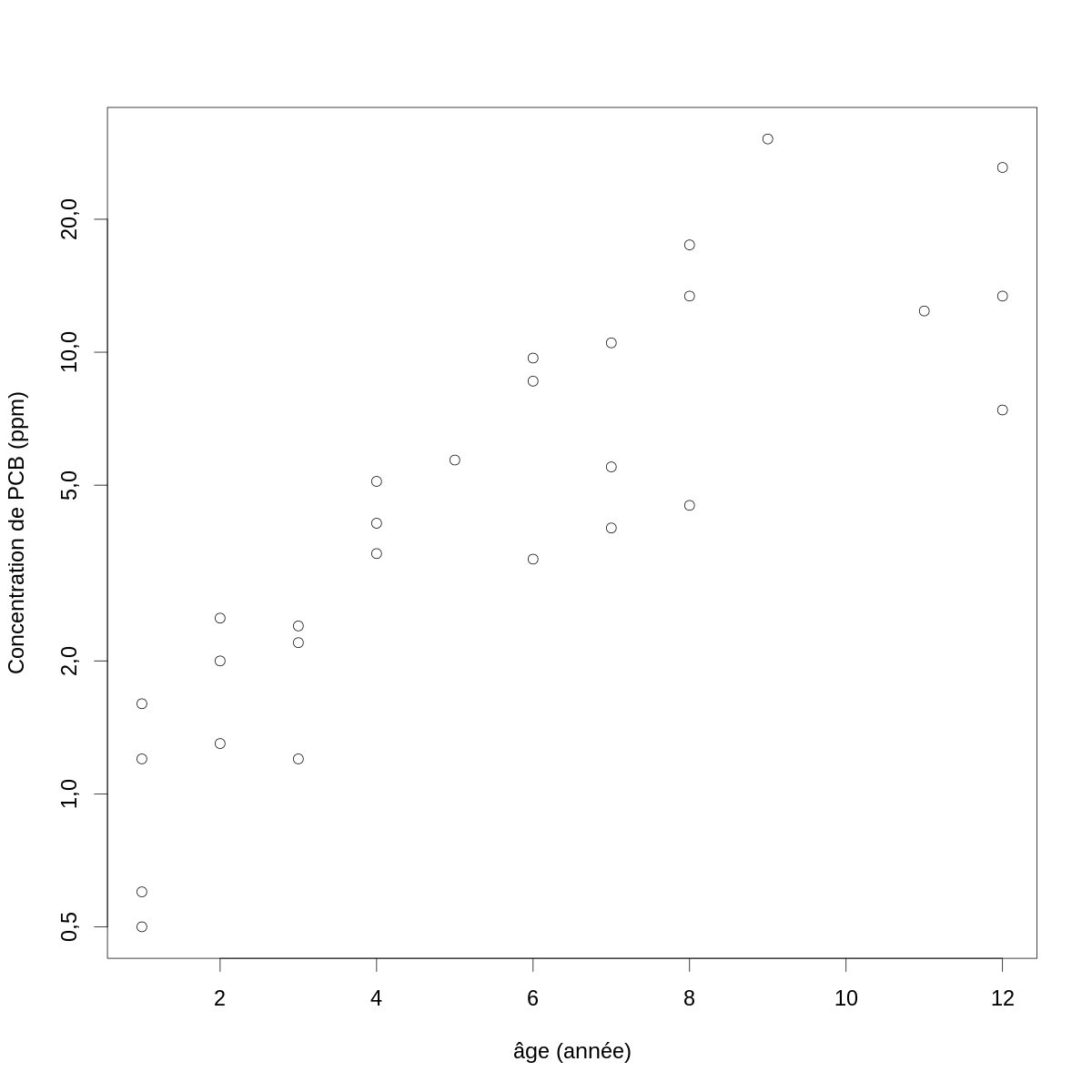
Figure 2 : Log (naturel) de la concentration de PCB en fonction de l'âge chez des poissons du lac Cayuga.
À ce stade vous avez peut-être l'impression que la courbe « qui passe à travers les points » serait légèrement concave (surtout pour les petites valeurs de l'abscisse). Ce que vous voudriez faire est écarter un peu les abscisses quand celles-ci sont petites et les rapprocher quand elles sont grandes, c'est-à-dire tester les mêmes transformations que précédemment. Avec la racine cubique nous obtenons :
par(cex=2) with(PCB,plot(age^(1/3), conc, xlab="Racine cubique de l'âge",ylab="Concentration de PCB (ppm)",log="y"))
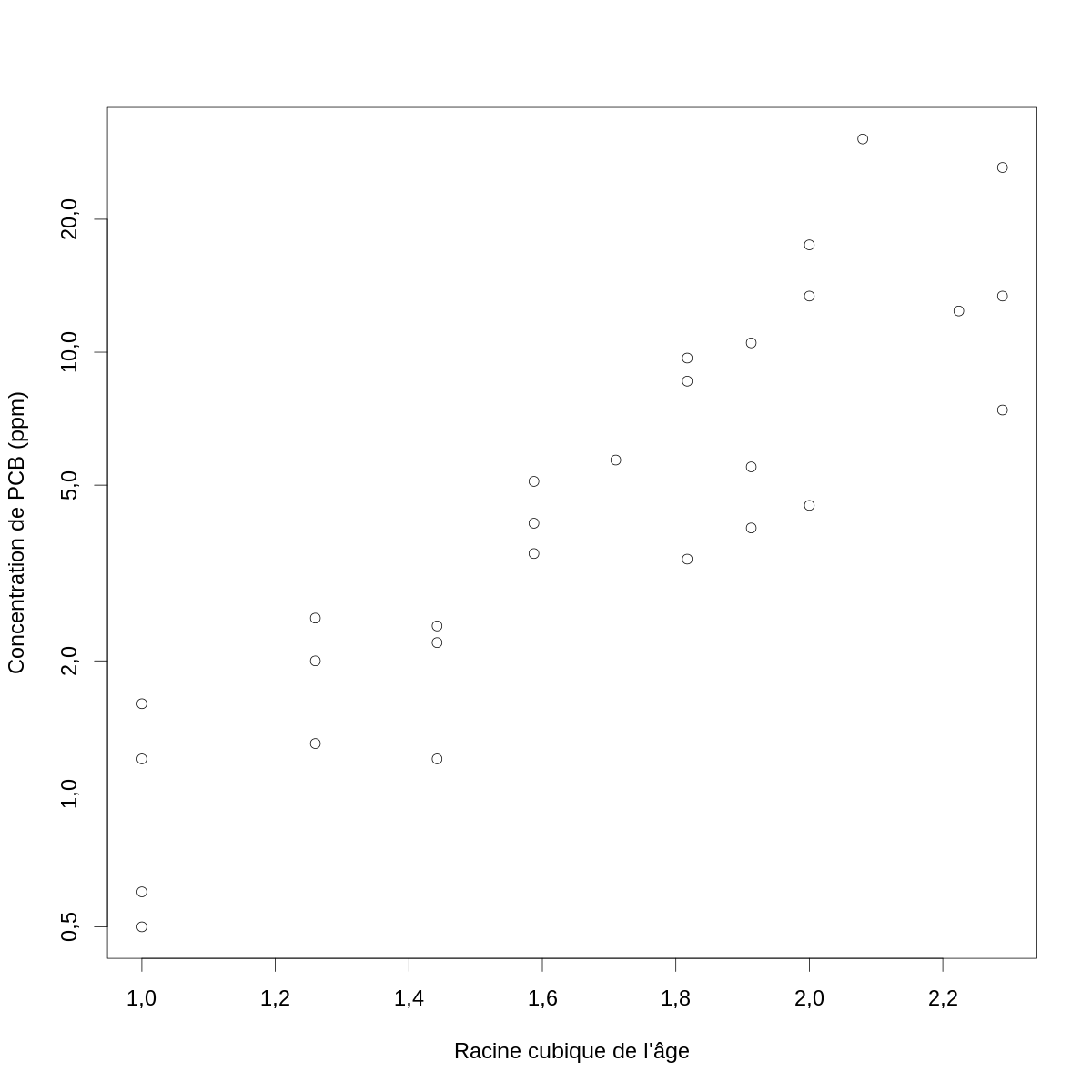
Figure 3 : Log (naturel) de la concentration de PCB en fonction de la racine cubique de l'âge chez des poissons du lac Cayuga.
2.2 Un exemple de régression linéaire par la méthode des moindres carrés
Nous allons considérer un jeu de données portant sur le test de dureté Janka qui est utilisé pour déterminer la résistance du bois : « il mesure la force nécessaire pour enfoncer dans le bois, jusqu'à la moitié de son diamètre, une bille d'acier de 11,284 mm (0,444 pouce). » (Wikipédia). Le jeu de données se trouve à l'adresse : http://www.uow.edu.au/~mwand/webspr/janka.txt sous forme d'un fichier texte (ASCII). Le jeu de donnée comprend 36 mesures effectuées sur des échantillons (de bois) d'Eucalyptus de densité variable. Le but des mesures est de déterminer la relation entre densité et dureté.
2.2.1 Téléchargement des données
Commençons par télécharger les données (avec la fonction wget) :
wget http://www.uow.edu.au/~mwand/webspr/janka.txt
2.2.2 Analyse avec R
Nous chargeons les données dans l'espace de travail :
janka <- read.table("janka.txt",header=TRUE)
| 24.7 | 484 |
| 24.8 | 427 |
| 27.3 | 413 |
| 28.4 | 517 |
| 28.4 | 549 |
| 29 | 648 |
| 30.3 | 587 |
| 32.7 | 704 |
| 35.6 | 979 |
| 38.5 | 914 |
| 38.8 | 1070 |
| 39.3 | 1020 |
| 39.4 | 1210 |
| 39.9 | 989 |
| 40.3 | 1160 |
| 40.6 | 1010 |
| 40.7 | 1100 |
| 40.7 | 1130 |
| 42.9 | 1270 |
| 45.8 | 1180 |
| 46.9 | 1400 |
| 48.2 | 1760 |
| 51.5 | 1710 |
| 51.5 | 2010 |
| 53.4 | 1880 |
| 56 | 1980 |
| 56.5 | 1820 |
| 57.3 | 2020 |
| 57.6 | 1980 |
| 59.2 | 2310 |
| 59.8 | 1940 |
| 66 | 3260 |
| 67.4 | 2700 |
| 68.8 | 2890 |
| 69.1 | 2740 |
| 69.1 | 3140 |
Le jeu de données n'étant pas trop grand, nous pouvons l'afficher dans son ensemble :
janka
dens hardness 1 24,7 484 2 24,8 427 3 27,3 413 4 28,4 517 5 28,4 549 6 29,0 648 7 30,3 587 8 32,7 704 9 35,6 979 10 38,5 914 11 38,8 1070 12 39,3 1020 13 39,4 1210 14 39,9 989 15 40,3 1160 16 40,6 1010 17 40,7 1100 18 40,7 1130 19 42,9 1270 20 45,8 1180 21 46,9 1400 22 48,2 1760 23 51,5 1710 24 51,5 2010 25 53,4 1880 26 56,0 1980 27 56,5 1820 28 57,3 2020 29 57,6 1980 30 59,2 2310 31 59,8 1940 32 66,0 3260 33 67,4 2700 34 68,8 2890 35 69,1 2740 36 69,1 3140
Comme toujours, la première chose à faire est une figure de la variable à expliquer en fonction de la (des) variable(s) explicatives (ou prédictives) :
par(cex=2) with(janka,plot(dens,hardness,col="blue",xlab="Densité",ylab="Dureté")) grid(10,10,lwd=2)
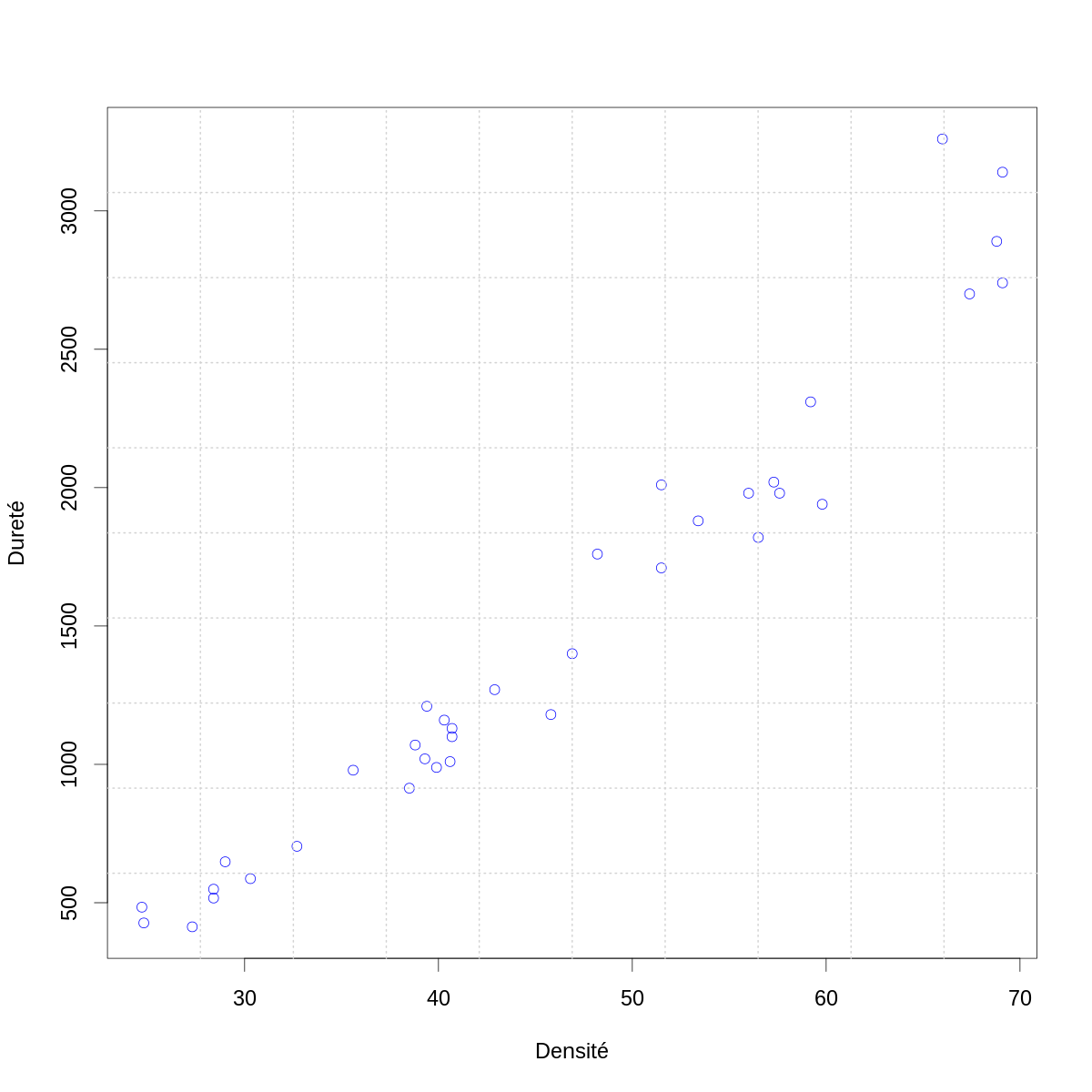
Figure 4 : La dureté (résultat du test de dureté de Janka) en fonction de la densité pour un échantillon d'eucalyptus.
On peut remarquer plusieurs choses :
- la densité apparaît comme un bon prédicteur de la dureté ;
- la variance de la dureté semble augmenter avec la densité ;
- la « fonction de régression » semble être légèrement incurvée vers le haut pour les plus grandes valeurs de la densité.
2.2.2.1 Matrice \(\mathbf{X}\) du plan d'expérience
La matrice « du plan d'expérience » est la matrice \(\mathbf{X}\) de l'équation : \[\mathbf{Y} = \mathbf{X} \, \mathbf{β} + \mathbf{Z} \; .\] Comme nous avons constaté une légère courbure sur le graphe précédent, nous allons inclure dans notre modèle un terme proportionnel au carré de la densité en plus d'un terme proportionnel à la densité — nous n'oublions pas non plus d'inclure une colonne de 1 pour l'ordonnée à l'origine — ce qui nous donne :
X <- cbind(rep(1,dim(janka)[1]),janka$dens,janka$dens^2)
| 1 | 24.7 | 610.09 |
| 1 | 24.8 | 615.04 |
| 1 | 27.3 | 745.29 |
| 1 | 28.4 | 806.56 |
| 1 | 28.4 | 806.56 |
| 1 | 29 | 841 |
| 1 | 30.3 | 918.09 |
| 1 | 32.7 | 1069.29 |
| 1 | 35.6 | 1267.36 |
| 1 | 38.5 | 1482.25 |
| 1 | 38.8 | 1505.44 |
| 1 | 39.3 | 1544.49 |
| 1 | 39.4 | 1552.36 |
| 1 | 39.9 | 1592.01 |
| 1 | 40.3 | 1624.09 |
| 1 | 40.6 | 1648.36 |
| 1 | 40.7 | 1656.49 |
| 1 | 40.7 | 1656.49 |
| 1 | 42.9 | 1840.41 |
| 1 | 45.8 | 2097.64 |
| 1 | 46.9 | 2199.61 |
| 1 | 48.2 | 2323.24 |
| 1 | 51.5 | 2652.25 |
| 1 | 51.5 | 2652.25 |
| 1 | 53.4 | 2851.56 |
| 1 | 56 | 3136 |
| 1 | 56.5 | 3192.25 |
| 1 | 57.3 | 3283.29 |
| 1 | 57.6 | 3317.76 |
| 1 | 59.2 | 3504.64 |
| 1 | 59.8 | 3576.04 |
| 1 | 66 | 4356 |
| 1 | 67.4 | 4542.76 |
| 1 | 68.8 | 4733.44 |
| 1 | 69.1 | 4774.81 |
| 1 | 69.1 | 4774.81 |
2.2.2.2 Décomposition QR
Ensuite, nous effectuons la décomposition QR de \(\mathbf{X}\), comme nous l'avons vu dans le cours d'Ihaka et dans le bouquin de Bates et Watts :
\[\mathbf{X} = \mathbf{Q} \, \mathbf{R} \; ,\]
où \(\mathbf{Q}\) est une matrice orthogonale n x p et où \(\mathbf{R}\) est triangulaire supérieure p x p. La décomposition QR est effectuée par la fonction qr qui renvoie une liste dont le premier composant qr est une matrice n x p qui contient « sous forme compacte », la matrice \(\mathbf{R}\) et l'information nécessaire à la construction de \(\mathbf{Q}\). Ces deux dernières matrices sont extraites au moyen des fonctions qr.R et qr.Q appliquées à la liste retournée par qr (pour plus de détails, tapez ?qr en ligne de commande) :
XdecompQR <- qr(X) Q <- qr.Q(XdecompQR)
R <- qr.R(XdecompQR)
| -6 | -274.4 | -13625.0033333333 |
| 0 | 80.3408986755812 | 7586.66501596641 |
| 0 | 0 | -1032.05530547884 |
On vérifie simplement que la matrice Q est de bonne dimension :
dim(Q)
[1] 36 3
et qu'elle est othogonale :
t(Q) %*% Q
[,1] [,2] [,3]
[1,] 1,000000e+00 -5,551115e-17 5,551115e-17
[2,] -5,551115e-17 1,000000e+00 1,665335e-16
[3,] 5,551115e-17 1,665335e-16 1,000000e+00
2.2.2.3 Estimateur des moindres carrés
Maintenant nous pouvons obtenir l'estimateur \(\hat{β}\) des moindres carrés, c'est-à-dire, le vecteur \(β\) qui minimise :
\[(\mathbf{Y} - \mathbf{X} \, \mathbf{β})^{T} \, (\mathbf{Y} - \mathbf{X} \, \mathbf{β})\, \]
qui est aussi, comme nous l'avons vu solution de :
\[\mathbf{X}^{T} \, (\mathbf{Y} - \mathbf{X} \, \hat{β}) = \mathbf{0} \; ,\]
avec le développement suivant :
\[\begin{array}{l l l}
\mathbf{X}^{T} \, \mathbf{Y} & = & \mathbf{X}^{T} \, \mathbf{X} \, \hat{β} \\
\mathbf{R}^{T} \, \mathbf{Q}^{T} \, \mathbf{Y} & = & \mathbf{R}^{T} \, \mathbf{Q}^{T} \, \mathbf{Q} \, \mathbf{R} \, \hat{β} \\
\mathbf{R}^{T} \, \mathbf{Q}^{T} \, \mathbf{Y} & = & \mathbf{R}^{T} \, \mathbf{R} \, \hat{β} \quad (\mathbf{Q}^{T} \, \mathbf{Q} = \mathbf{I})\\
\mathbf{Q}^{T} \, \mathbf{Y} & = & \mathbf{R} \, \hat{β}
\end{array}\]
où nous avons utilisé, pour le passage de l'avant dernière à la dernière ligne, le fait que, si le rang du sous-espace vectoriel engendré par les colonnes de \(\mathbf{X}\) est p, alors \(\mathbf{R}\) et sa transposée sont invertibles. Après avoir effectué la décomposition QR d'une matrice on peut vérifier que le champ rank de la liste retournée est bien égale au nombre de colonnes de la matrice de départ :
XdecompQR$rank
[1] 3
À ce stade, nous avons encore besoin de savoir que R dispose d'une fonction adaptée à la solution de système d'équations linéaires dont la matrice des coefficients est triangulaire, il s'agit de la fonction backsolve, nous obtenons donc :
(beta.chapeau <- backsolve(R, t(Q) %*% janka$hardness))
[,1]
[1,] -118.0073759
[2,] 9.4340214
[3,] 0.5090775
2.2.2.4 Tests d'adéquation
La première chose à faire à ce stade est de rajouter la courbe ajustée aux données sur une figure :
par(cex=2) with(janka,plot(dens,hardness,col="blue",xlab="Densité",ylab="Dureté")) domaine.densite <- range(janka$dens) dd <- seq(domaine.densite[1],domaine.densite[2],len=501) lines(dd,cbind(rep(1,501),dd,dd^2) %*% beta.chapeau,col="red",lwd=2)
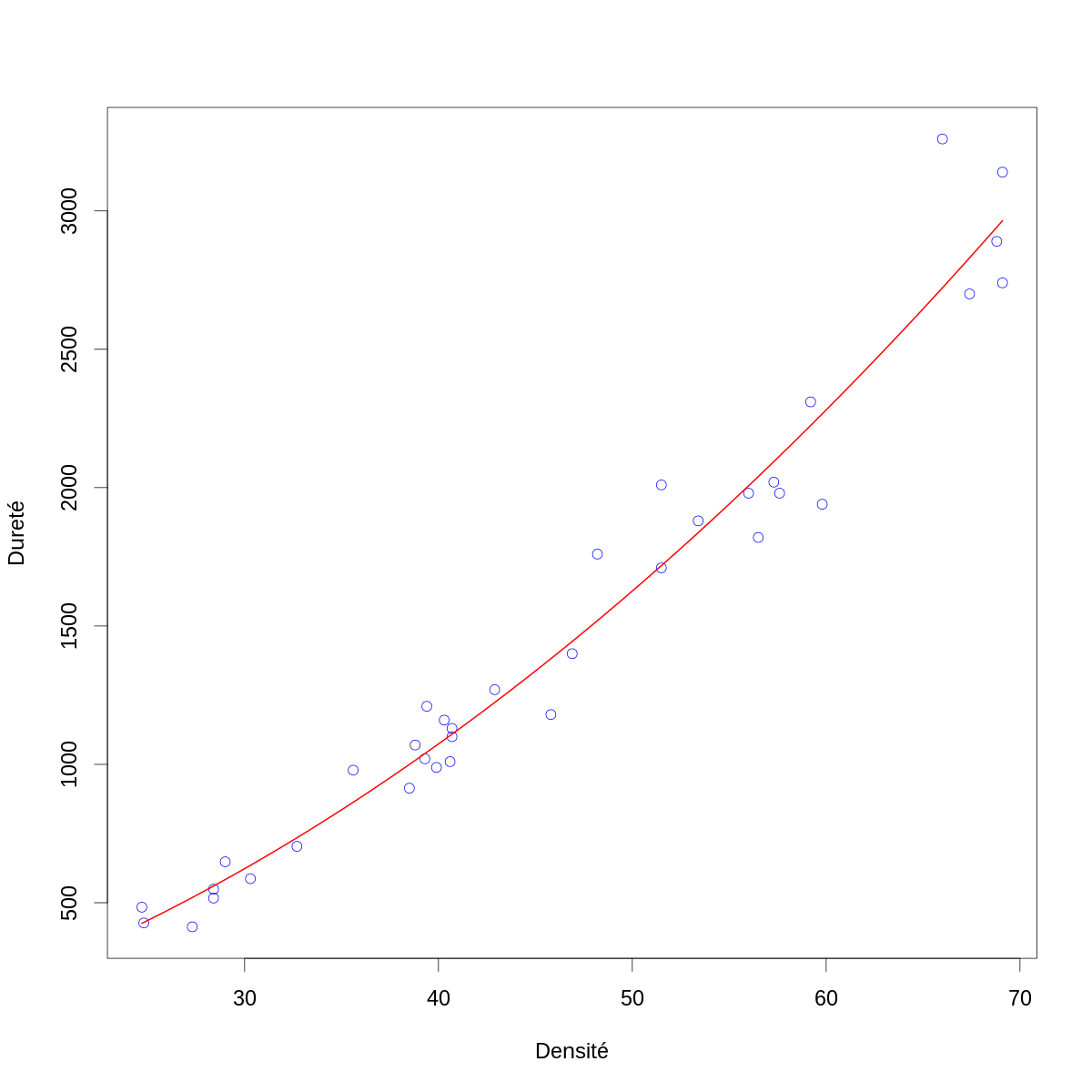
Figure 5 : La dureté (résultat du test de dureté de Janka) en fonction de la densité pour un échantillon d'eucalyptus (cercles bleus) avec modèle linéaire ajusté par la méthode des moindres carrés (courbe rouge).
À ce stade aucune « pathologie majeure » n'est visible. Nous devons encore construire deux graphes obligatoires :
- les résidus, \(\hat{\mathbf{Z}} \equiv \mathbf{Y} - \mathbf{X} \, \hat{β}\) en fonction des valeurs ajustées ou prédites, \(\hat{\mathbf{Y}} \equiv \mathbf{X} \, \hat{β}\) ;
- un diagramme Quantile-Quantile avec les quantiles d'une loi normale centrée réduite en abscisse et les quantiles des résidus en ordonnée.
Y.chapeau <- X %*% beta.chapeau Z.chapeau <- janka$hardness - Y.chapeau layout(matrix(1:2,nr=2)) par(cex=2) plot(Y.chapeau, Z.chapeau, col="blue",xlab="Valeurs prédites",ylab="Résidus") abline(h=0,col="red",lwd=2) qqnorm(Z.chapeau, col="blue",main="", xlab="Quantiles théoriques (loi normale)",ylab="Quantiles empiriques") qqline(Z.chapeau,col="red",lwd=2)
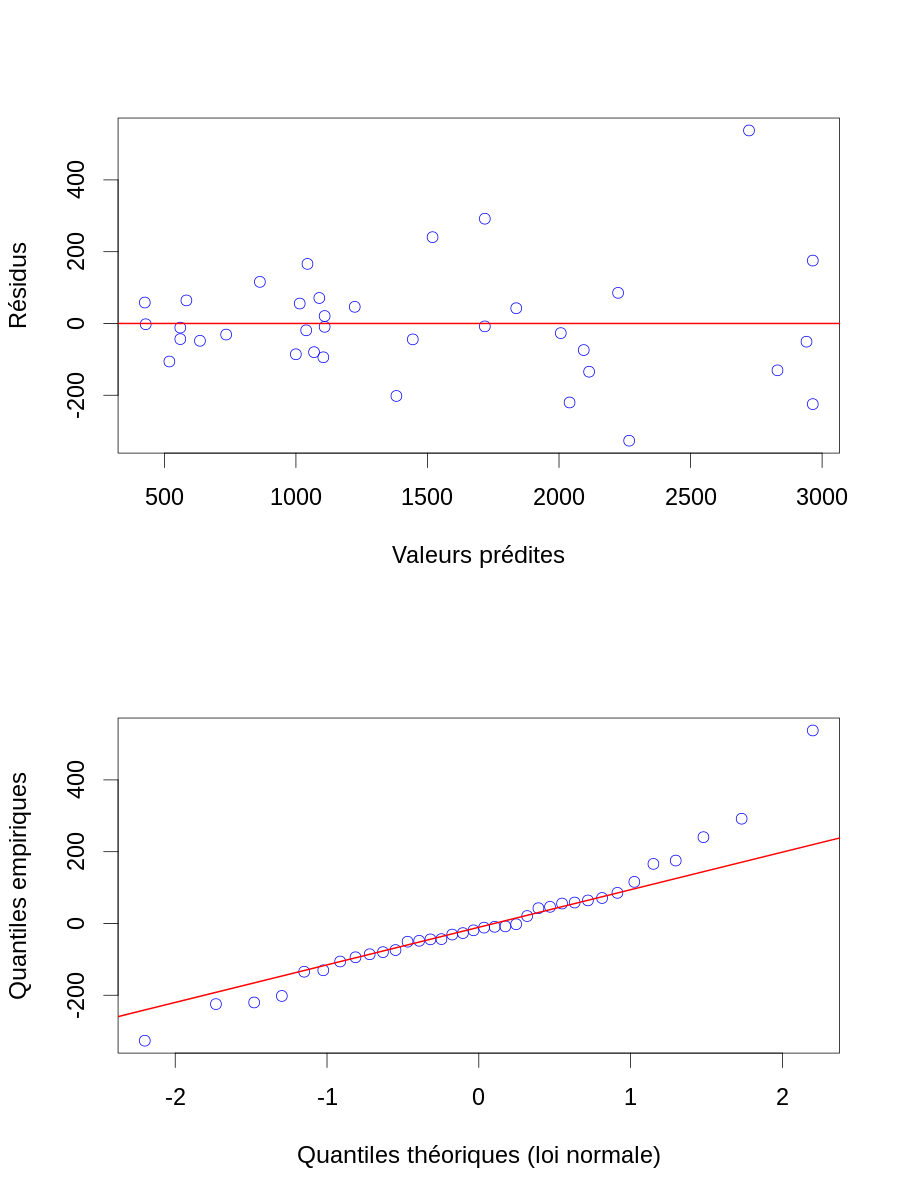
Figure 6 : Résidus en fonction des valeurs prédites (en haut) et diagramme quantile-quantile des résidus (en bas) pour les données de dureté (résultat du test de dureté de Janka) en fonction de la densité pour un échantillon d'eucalyptus. Les valeurs prédites viennent d'un modèle linéaire ajusté par la méthode des moindres carrés.
2.2.2.5 Critique et modification du modèle initial
2.2.2.5.1 Transformation des variables
Comme nous l'avions deviné lors de notre première visualisation des données, les résidus ne sont pas homogènes, ils fluctuent plus pour de grandes valeurs prédites que pour des petites. La stratégie classique est d'essayer de transformer la variable prédite afin d'homogénéiser sa variance ; par exemple avec une transformation log. On peut aussi en profiter pour transformer les variables explicatives afin d'avoir une ordonnée à l'origine qui a plus de sens, ce qu'on peut obtenir en travaillant avec la dureté centrée sur sa moyenne :
Xb <- cbind(rep(1,dim(janka)[1]),janka$dens-mean(janka$dens),(janka$dens-mean(janka$dens))^2) Yb <- log(janka$hardness) XbdecompQR <- qr(Xb) Qb <- qr.Q(XbdecompQR) Rb <- qr.R(XbdecompQR) (beta.chapeau.b <- backsolve(Rb, t(Qb) %*% Yb))
[,1]
[1,] 7.2298939843
[2,] 0.0436978417
[3,] -0.0005227877
2.2.2.5.2 Tests d'adéquation
Ce qui nous donne la figure :
Yb.chapeau <- Xb %*% beta.chapeau.b Zb.chapeau <- Yb - Yb.chapeau layout(matrix(1:3,nr=3)) par(cex=2) plot(janka$dens,Yb,col="blue",xlab="Densité",ylab="log(Dureté)") ddb <- seq(domaine.densite[1],domaine.densite[2],len=501)-mean(janka$dens) lines(dd,cbind(rep(1,501),ddb,ddb^2) %*% beta.chapeau.b,col="red",lwd=2) plot(Yb.chapeau, Zb.chapeau, col="blue",xlab="Valeurs prédites",ylab="Résidus") abline(h=0,col="red",lwd=2) qqnorm(Zb.chapeau, col="blue",main="", xlab="Quantiles théoriques (loi normale)",ylab="Quantiles empiriques") qqline(Zb.chapeau,col="red",lwd=2)
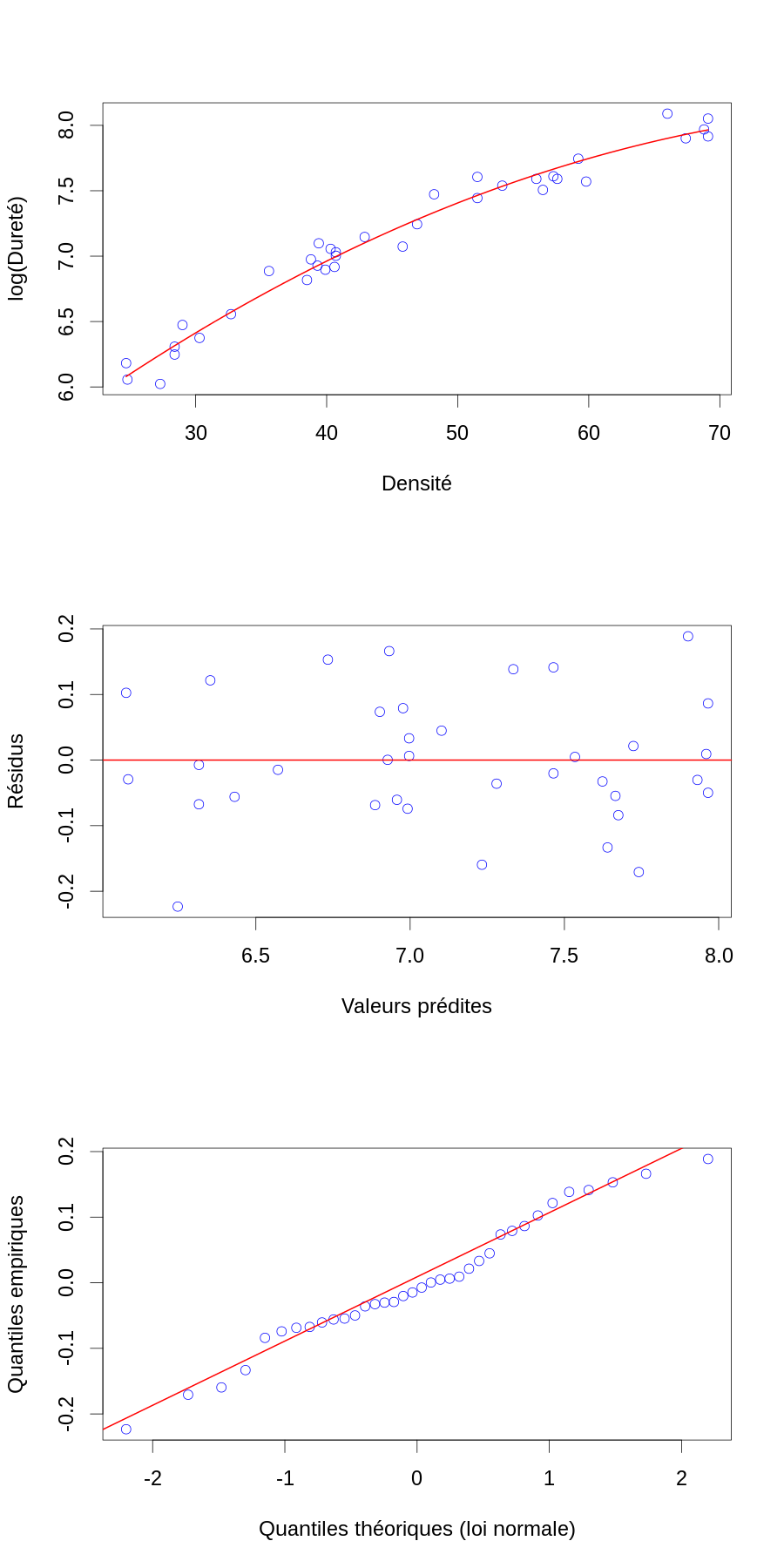
Figure 7 : En haut, le logarithme de la dureté (résultat du test de dureté de Janka) en fonction de la densité pour un échantillon d'eucalyptus (cercles bleus) avec modèle linéaire ajusté par la méthode des moindres carrés (courbe rouge). Au milieu, résidus en fonction des valeurs prédites. En bas, diagramme quantile-quantile des résidus.
2.2.2.6 Intervalles de confiance des paramètres
Une fois qu'un modèle en bonne adéquation avec les données a été obtenu, et seulement à ce moment là, on peut se mettre à calculer des intervalles de confiances sur les paramètres — les hypothèses faites pour dériver ces intervalles supposent en effet que le « modèle est bon », c'est donc une erreur, ou pour le moins une attitude très optimiste, d'appliquer une théorie donnant des intervalles de confiance reposant sur des hypothèses fausses. Plus concrètement, si notre modèle et bon nous avons :
\[\mathbf{Y} = \mathbf{X} \, \mathbf{β} + \mathbf{Z} \; .\]
L'estimateur des moindres carrés est quant à lui défini par :
\[\hat{β} \equiv (\mathbf{X}^{T} \, \mathbf{X})^{-1} \, \mathbf{X}^{T} \, \mathbf{Y} \; ,\]
d'où en substituant \(\mathbf{Y} = \mathbf{X} \, \mathbf{β} + \mathbf{Z}\) et en simplifiant :
\[\hat{β} = β + (\mathbf{X}^{T} \, \mathbf{X})^{-1} \, \mathbf{X}^{T} \, \mathbf{Z} \; .\]
Notez bien que pour en arriver là nous n'avons fait qu'une seule hypothèse : le sous-espace vectoriel engendré par les p colonnes de \(\mathbf{X}\) est de rang p (dit autrement, les p colonnes de \(\mathbf{X}\) sont linéairement indépendantes). Nous rajoutons maintenant une hypothèse sur \(\mathbf{Z}\) :
\[\mathbf{Z} \equiv (z_1,\ldots,z_n)^{T} \quad \textrm{avec} \quad z_{1,\ldots,n} \sim \mathcal{N}(0,σ^2) \quad \textbf{et IID} \; .\]
La matrice de variance-covariance de \(\mathbf{Z}\), définie par (l'espérance du produit externe des écarts à la moyenne) :
\[\textrm{Var}[\mathbf{Z}] \equiv \textrm{E}\left[\left(\mathbf{Z} - \textrm{E}[\mathbf{Z}]\right) \, \left(\mathbf{Z} - \textrm{E}[\mathbf{Z}]\right)^{T} \right]\]
et alors
\[\textrm{Var}[\mathbf{Z}] = σ^2 \, I_n \; ,\]
où \(I_n\) désigne la matrice identité de \(\mathbb{R}^n\). D'où :
\[\textrm{Var}[\hat{β}] = σ^2 \, (\mathbf{X}^{T} \, \mathbf{X})^{-1} \; ,\]
soit en utilisant la décomposition QR de \(\mathbf{X}\) :
\[\textrm{Var}[\hat{β}] = σ^2 \, (\mathbf{R}^{T} \, \mathbf{R})^{-1} \; .\]
Écrit autrement :
\[\hat{β} \sim \mathcal{N}\left(β,σ^2 \, (\mathbf{R}^{T} \, \mathbf{R})^{-1} \right) \; .\]
Comme dans le général, en pratique, nous ne connaissons pas \(σ^2\), mais nous l'estimons par :
\[\hat{σ}^2 \equiv \frac{(\mathbf{Y} - \mathbf{X} \, \hat{β})^{T} \, (\mathbf{Y} - \mathbf{X} \, \hat{β})}{n-p} \; ,\]
nous avons (l'égalité n'est strictement vraie que quand \(n \rightarrow \infty\)) :
\[\hat{β} \approx \mathcal{N}\left(β,\hat{σ}^2 \, (\mathbf{R}^{T} \, \mathbf{R})^{-1} \right) \; .\]
Par contre nous avons pour tout n :
\[\frac{\hat{β}_i - β_i}{\hat{σ} \, \sqrt{(\mathbf{R}^{T} \, \mathbf{R})_{i,i}^{-1}}} \sim \mathcal{t}_{n-p} \quad \textrm{pour} \quad i=1,\ldots,p \; ,\]
où \(\mathcal{t}_{n-p}\) désigne la loi de student à n-p degrés de liberté.
Forts de ses résultats nous formons une matrice dont la première colonne est \(\hat{β}\), l'élément \(i\) de la deuxième est l'erreur type : \(\hat{σ} \, \sqrt{(\mathbf{R}^{T} \, \mathbf{R})_{i,i}^{-1}}\), l'élément \(i\) de la troisième et la statistique « \(t_i\) » : \(\hat{β}_i/\left(\hat{σ} \, \sqrt{(\mathbf{R}^{T} \, \mathbf{R})_{i,i}^{-1}}\right)\) et l'élément \(i\) de la quatrième est la probabilité d'observer une valeur plus grande ou égale à \(|t_i|\) si \(β_i = 0\) :
sigma2.chapeau.b <- sum(Zb.chapeau^2)/-diff(dim(Xb)) beta.chapeau.b.se <- sqrt(sigma2.chapeau.b*diag(solve(t(Rb) %*% Rb))) beta.chapeau.b.t <- beta.chapeau.b/beta.chapeau.b.se beta.chapeau.b.p <- pt(abs(beta.chapeau.b.t),-diff(dim(Xb)),lower.tail=FALSE) beta.chapeau.b.resume <- cbind(beta.chapeau.b, beta.chapeau.b.se, beta.chapeau.b.t, beta.chapeau.b.p) colnames(beta.chapeau.b.resume) <- c("est","se","t","p") round(beta.chapeau.b.resume, digits=3)
est se t p
[1,] 7.230 0.024 298.015 0
[2,] 0.044 0.001 33.947 0
[3,] -0.001 0.000 -5.354 0
2.2.2.7 Faire tout cela en une seule ligne de commande de R
R étant un logiciel très orienté vers la statistique, il dispose d'une fonction, lm, qui nous permet de faire tout, ou presque, ce que nous venons de faire en une seule ligne de commande. Vous pouvez voir en fait ce qui précède comme une « décomposition » de ce que lm fait en interne.
janka <- transform(janka,d=dens-mean(dens)) janka.lm <- lm(log(hardness) ~ d + I(d^2), data=janka) summary(janka.lm)
Call:
lm(formula = log(hardness) ~ d + I(d^2), data = janka)
Residuals:
Min 1Q Median 3Q Max
-0.22331 -0.05708 -0.01104 0.07500 0.18871
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.230e+00 2.426e-02 298.015 < 2e-16 ***
d 4.370e-02 1.287e-03 33.947 < 2e-16 ***
I(d^2) -5.228e-04 9.764e-05 -5.354 6.49e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1008 on 33 degrees of freedom
Multiple R-squared: 0.9723, Adjusted R-squared: 0.9706
F-statistic: 578.9 on 2 and 33 DF, p-value: < 2.2e-16
L'objet de classe lm janka.lm retourné par l'appel à lm ci-dessus peut-être directement passé comme argument de la fonction générique plot pour générer les graphes d'adéquations que nous avons fait précédemment ainsi que pas mal d'autres. Sur ces graphes, vous pourrez consulter le bouquin de Lafaye de Micheaux, Drouilhet et Liquet donné en référence du cours, ainsi que Residuals and Influence in Regression de Cook et Weisberg. J'ai trouvé l'exemple que nous venons d'explorer dans le bouquin An introduction to R: software for statistical modelling and computing, course notes de Kuhnert et Venables (p. 111-118).
Faites attention au fait que je n'ai pas discuter ici du problème de la sélection de variables (dit autrement de la construction de \(\mathbf{X}\)) dans les cas où de nombreuses données / valeurs de variables sont disponibles pour chaque individu. En effet, le choix des variables utiles pour la prédiction se pose alors très vite. Ce problème important et discuté dans le bouquin de Lafaye de Micheaux et col. ainsi que dans The Elements of Statistical Learning de Hastie, Tibshirani et Friedman.
2.2.2.8 Pourquoi s'embêter à homogénéiser la variance ?
Nous venons de voir que nos calculs d'intervalles de confiance sur \(\hat{β}\) repose sur l'hypothèse « normale IID de variance \(σ^{2}\) » des éléments de \(\mathbf{Z}\). Une façon de voir l'effet de déviations par-rapport à cette hypothèse est :
- prendre les
beta.chapeau.betsigma2.chapeau.bcomme les « vraies valeurs » dans une séries de simulations, disons 1000, où des observations \(\mathbf{Y}\) sont simulées suivant \(\log(\mathbf{Y}) \sim \mathcal{N}\left(\mathbf{X}_{b} \, \hat{β}_{b}, \hat{σ}_{b}^2 I_{n} \right)\) ; - pour chaque observation simulée \(\mathbf{y}^{(i)}\) (vecteur à
ncomposants) on calcule un \(\hat{β}^{(i)} = (\mathbf{X}^{T} \, \mathbf{X})^{-1} \, \mathbf{X}^{T} \, \mathbf{y}^{(i)}\) et un \(\hat{σ}^{2,(i)} = (\mathbf{y}^{(i)} - \mathbf{X} \, \hat{β}^{(i)})^{T} (\mathbf{y}^{(i)} - \mathbf{X} \, \hat{β}^{(i)}) / (n-p)\) avant de calculer \(m^{(i)} \equiv (\hat{β}^{(i)} - \hat{β})^{T} \, (\mathbf{R}^{T} \, \mathbf{R}) \, (\hat{β}^{(i)} - \hat{β}) / \hat{σ}^{2,(i)}\) et on calcule de même \(\hat{β}_{b}^{(i)} = (\mathbf{X}_{b}^{T} \, \mathbf{X}_{b})^{-1} \, \mathbf{X}_{b}^{T} \, \log(\mathbf{y}^{(i)})\) et un \(\hat{σ}_{b}^{2,(i)} = (\log(\mathbf{y}^{(i)}) - \mathbf{X}_{b} \, \hat{β}_{b}^{(i)})^{T} (\log(\mathbf{y}^{(i)}) - \mathbf{X}_{b} \, \hat{β}_{b}^{(i)}) / (n-p)\) avant de calculer \(m_{b}^{(i)} \equiv (\hat{β}_{b}^{(i)} - \hat{β}_{b})^{T} \, (\mathbf{R}_{b}^{T} \, \mathbf{R}_{b}) \, (\hat{β}_{b}^{(i)} - \hat{β}_{b}) / \hat{σ}_{b}^{2,(i)}\) ; - \(m_{b}^{(i)}/p\) devrait suivre la loi Fisher (ou Fisher-Snedector) à
p= 3 etn-p= 33 degrés de liberté alors que les \(m^{(i)}/p\) devrait s'en écarter.
Nous commençons par simuler les données :
set.seed(20110928,"Mersenne-Twister") nrep <- 1000 n <- dim(Xb)[1] logYvrai <- as.vector(Xb %*% beta.chapeau.b) logY <- logYvrai + matrix(rnorm(nrep*n)*sqrt(sigma2.chapeau.b), nr=n,nc=nrep)
Puis nous effectuons les calculs :
NmP <- -diff(dim(X)) p <- dim(X)[2] RtransposexRb <- t(Rb) %*% Rb beta.chapeau.centre <- backsolve(Rb, t(Qb) %*% janka$hardness) mV <- apply(logY,2, function(lY) { Y <- exp(lY) beta.circonflexe <- backsolve(Rb, t(Qb) %*% Y) s2 <- sum((Y - X %*% beta.circonflexe)^2) / NmP delta.beta <- beta.circonflexe - beta.chapeau.centre t(delta.beta) %*% RtransposexRb %*% delta.beta / s2 / p}) mVb <- apply(logY,2, function(lY) { Y <- lY beta.circonflexe <- backsolve(Rb, t(Qb) %*% Y) s2 <- sum((Y - Xb %*% beta.circonflexe)^2) / NmP delta.beta <- beta.circonflexe - beta.chapeau.b t(delta.beta) %*% RtransposexRb %*% delta.beta / s2 / p})
Ici j'ai aussi utilisé la version « centrée » de la densité pour l'ajustement sur la dureté. Ce qui nous donne la figure :
layout(matrix(1:2,nr=2)) par(cex=2) ff <- qf(ppoints(1000),3,33) plot(range(ff),range(mV),type="n", xlab="Quantiles d'une loi de Fisher à 3 et 33 degrés de liberté", ylab="Quantiles empiriques") points(ff,sort(mV),pch=".") plot(range(ff),range(mVb),type="n", xlab="Quantiles d'une loi de Fisher à 3 et 33 degrés de liberté", ylab="Quantiles empiriques") abline(a=0,b=1,col="red",lwd=2) points(ff,sort(mVb),pch=".")
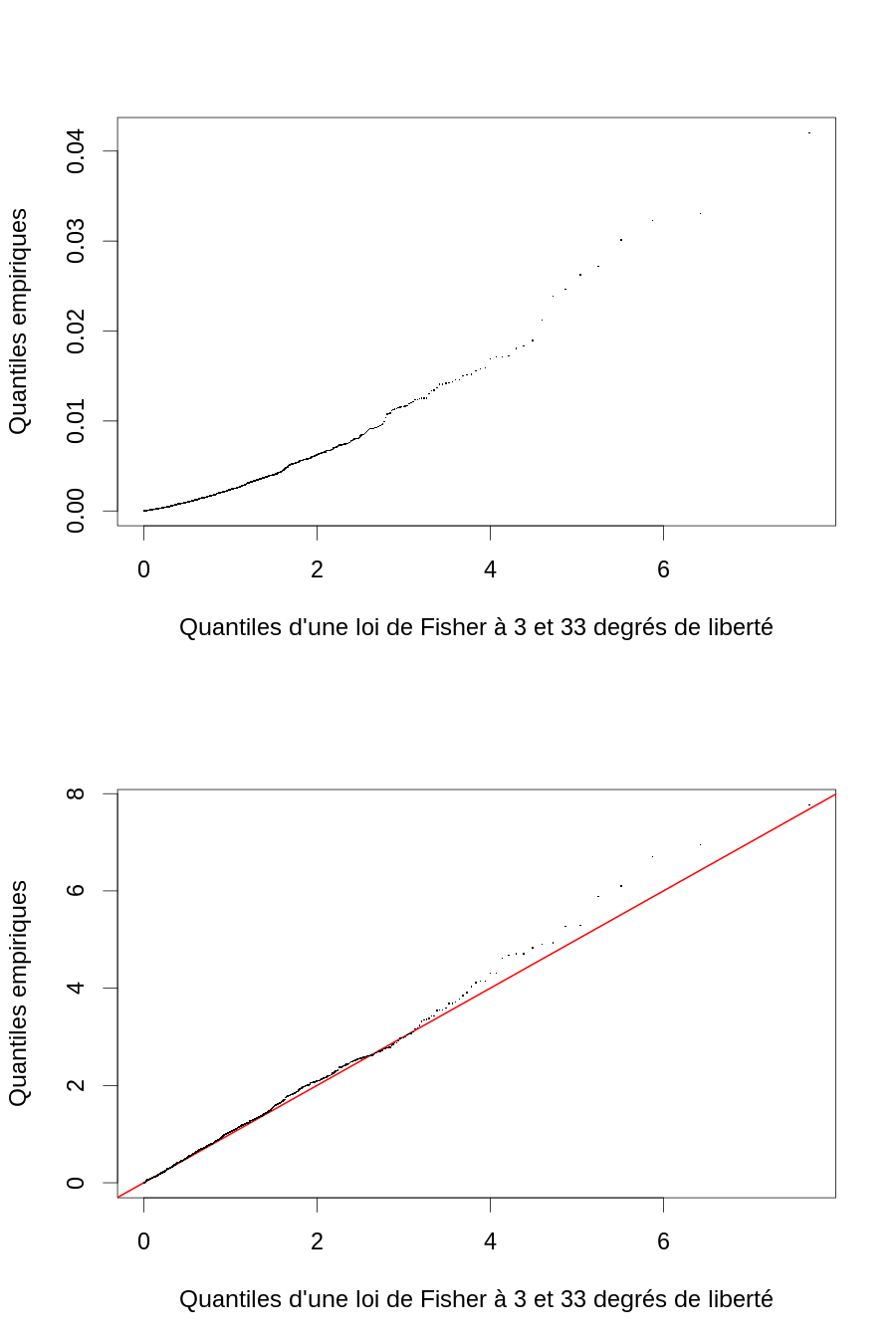
Figure 8 : Diagramme quantile-quantile des écarts normalisés des estimations de β à β lorsque le mauvais modèle est utilisé (en haut) et lorsque le bon modèle est utilisé (en bas).
Le problème avec l'ajustement sur la dureté (par opposition avec l'ajustement sur la log(dureté)) est que la variance se trouve fortement surestimée.
En exercice complémentaire, vous pourrez calculer les probabilités empiriques de recouvrement des intervalles de confiance à 95% pour chacun des trois paramètres du modèle dans les deux cas.
2.2.3 Analyse avec GNU octave
J'utilise ici GNU octave un logiciel libre qui ressemble beaucoup à Matlab.
Je commence par charger les données :
janka = dlmread("janka.txt") janka = janka(2:37,1:2)
Je construis ensuite la matrice du plan d'expérience :
X = [ones(36,1) janka(:,1) janka(:,1).^2]
J'obtiens la décomposition QR de celle-ci :
[Q,R] = qr(X)
Puis \(\hat{β}\) :
beta_chapeau = R(1:3,1:3)\(Q(:,1:3)'*janka(:,2)) ans = beta_chapeau
| -118.0073758808507 |
| 9.434021375904702 |
| 0.5090774624693807 |
GNU octave ne semble pas avoir l'équivalent de backsolve.
Je répète l'opération en travaillant avec la log(dureté) et en centrant la densité :
Xb = [ones(36,1) janka(:,1)-mean(janka(:,1)) (janka(:,1)-mean(janka(:,1))).^2] [Qb,Rb] = qr(Xb) beta_chapeau_b = Rb(1:3,1:3)\(Qb(:,1:3)'*log(janka(:,2))) ans = beta_chapeau_b
| 7.229893984289252 |
| 0.04369784165485691 |
| -0.0005227876890040932 |
Il suffit alors de continuer de la sorte pour obtenir des résultats équivalents, pour ne pas dire identiques, à ceux de R…
2.2.4 Analyse en Common Lisp
Les plus aventureux pourons jetter un oeil sur une manière de reproduire cette analyse en utilisant le Common Lisp.
3 L'estimation par « maximum de vraisemblance »
3.1 La fonction de vraisemblance
La vraisemblance ou fonction de vraisemblance (likelihood function) est la pierre angulaire des statistiques (paramétriques) modernes. Cette fonction est obtenue en « inversant » les rôles des observations et des paramètres dans un modèle probabiliste. Plus précisément, supposons que N est une variable aléatoire de loi de poisson, c.-à-d. que : \[ \mathrm{Pr}\left(N=n | λ\right) = \frac{λ^n}{n!} \, \exp(-λ),\quad \mathrm{avec} \quad x=0,1,\ldots \quad{et} \quad λ > 0 \; .\] Supposons aussi que nous observons n et que nous cherchons une estimation de λ basée sur cette observation et notre hypothèse sur le mécanisme de génération de données décrit par la loi de Poisson ; nous introduisons alors la fonction de vraisemblance : \[ \mathcal{L}(λ | n) \equiv \frac{λ^n}{n!} \, \exp(-λ),\quad \mathrm{avec} \quad x=0,1,\ldots \; .\] Attention \(\mathcal{L}\) est une fonction de λ, les données étant déjà observées et donc fixées. Cela implique que même si \(\mathrm{Pr}\left(N=n | λ\right)\) est normalisée (\(\sum_{n=0}^{\infty} \mathrm{Pr}\left(N=n|λ \right) = 1\)), aucune contrainte de ce type n'existe pour \(\mathcal{L}\) !
Supposons que X est une variable aléatoire de loi exponentielle, c'est-à-dire que : \[ \mathrm{Pr}\left(X \in [x-δ/2,x+δ/2] | τ\right) = \int_{x-δ/2}^{x+δ/2} exp(-u/τ)/τ \, du\; \quad \mathrm{avec} \quad x \ge 0 \quad \mathrm{et} \quad τ > 0 \; ,\] que nous observons x avec une précision δ (\(δ \ll τ\)) et que nous voulons estimer τ, basé sur x et sur notre modèle. Nous introduisons alors la fonction de vraisemblance : \[\mathcal{L}(τ | x,δ) \equiv exp(-x/τ)/τ \, δ \; \quad \mathrm{avec} \quad x \ge 0 \quad \mathrm{et} \quad τ > 0 \; ,\] qui est une fonction de τ, les données étant observées et donc fixées. De même que dans le cas de la variable aléatoire discrète précédente, il n'y a pas de contrainte de normalisation sur \(\mathcal{L}(τ | x,δ)\). Il est d'usage de « laisser tomber » le facteur δ lié à la précision de la mesure et ainsi d'écrire : \[\mathcal{L}(τ | x) \equiv exp(-x/τ)/τ \; \quad \mathrm{avec} \quad x \ge 0 \quad \mathrm{et} \quad τ > 0 \; .\] En général, cela ne pose pas de problème mais il faut quand même garder à l'esprit que cette simplification a été faite lorsqu'on rassemble des données collectées avec deux appareils de mesure de précisions différentes. Dans ce dernier cas, laissez tomber le δ n'est plus acceptable puisque cela revient, implicitement, à considérer que la précision des mesures et la même pour les deux jeux de données.
3.2 La fonction de log-vraisemblance
Comme son nom l'indique la fonction de log-vraisemblance est le logarithme (naturel) de la fonction de vraisemblance. Comme nous allons souvent (toujours en pratique) utiliser la vraisemblance sur un ordinateur et que celle-ci peut être soit très grande en valeur absolue soit très petite, on a tout intérêt pour des raisons de précision numérique à travailler avec la log-vraisemblance.
3.3 L'estimateur du maximum de vraisemblance
Lorsqu'on dispose de données \(x_1,x_2,\ldots,x_n\) supposées IID de densité de probabilité \(p(X=x|θ)\), la log-vraisemblance devient :
\[l(θ) = \sum_{i=1}^n \log p(x_i|θ)\]
et l'estimateur du maximum de vraisemblance, \(\hat{θ}\), est par définition :
\[\hat{θ} \equiv \arg \max_{θ} \, l(θ) \; .\]
Quelques remarques :
- la fonction logarithme étant strictement croissante, maximiser la log-vraisemblance va donner le même \(\hat{θ}\) que maximiser la vraisemblance ;
- on peut « se débarrasser », dans la définition de la (log-)vraisemblance, de tous les termes ne faisant pas intervenir les paramètres, dès lors qu'on cherche \(\hat{θ}\) ;
- choisir l'estimateur du maximum de vraisemblance revient à choisir à posteriori la valeur du (vecteur de) paramètre(s) qui donne la plus grande (densité de) probabilité aux données observées, ce qui ne semble intuitivement pas absurde.
3.4 Fonctions associées à la fonction de log-vraisemblance
La fonction score est la dérivée premières (le gradient) de la fonction de log-vraisemblance : \[S(θ) = \frac{\partial l(θ)}{\partial θ} \; .\] L'information observée (observed information) est l'opposée de la dérivée seconde (le « hessien ») de la fonction de log-vraisemblance : \[\mathcal{J}(θ) = - \nabla \nabla^T l(θ) \; .\] L'information observée normalisée est l'information observé divisée par le nombre d'observations : \[\mathcal{J}_n(θ) = - \frac{1}{n} \, \nabla \nabla^T l(θ) \; .\] L'information de Fisher (Fisher information) est l'espérance par-rapport à la vraie densité de l'information observée normalisée : \[\mathcal{I}(θ) = \mathrm{E} \mathcal{J}_n(θ) \; .\] Pour une value de θ fixée, la fonction score est un vecteur aléatoire et l'information observée est une matrice aléatoire. L'information de Fisher étant définie comme une espérance est une matrice non aléatoire.
3.5 Ce que dit la théorie
- si les \(x_1,x_2,\ldots,x_n\) sont
IIDde densité de probabilité \(p(X=x|θ_0)\) ; - si l'espace des paramètres Θ est compact ;
- si le modèle est identifiable, c'est-à-dire si \(p(\;|θ) \neq p(\;|θ_0)\) pour tout \(θ \neq θ_0\) ;
- si on peut échanger intégration et différentiation dans « des expressions du type » : \(\frac{\partial}{\partial θ} \sum_i \int \log \left(p(x_{i}|θ)\right) \, p(x_{i}|θ_0) \, dx_i\)
alors \(\hat{θ}\) converge en probalilité vers θ0. De plus si :
- θ0 est un point intérieur de Θ ;
- \(p(x|θ)\) considérée comme fonction de θ est > 0 et est deux fois continûment différentiable dans un voisinage de θ0 ;
- quelques autres condition plus techniques spécifiées à l'adresse suivante sont vérifiées ;
alors : \[ \sqrt{n} \left(\hat{θ}-θ_0 \right) \stackrel{\mathrm{loi}}{\rightarrow} \mathcal{N}\left(0,\mathcal{I}^{-1}(θ_0)\right) \; .\] En pratique, comme l'information observée normalisée converge en probabilité vers l'information de Fisher on utilise : \[ \sqrt{n} \left(\hat{θ}-θ_0 \right) \stackrel{\mathrm{loi}}{\rightarrow} \mathcal{N}\left(0,\mathcal{J}_n^{-1}(\hat{θ})\right) \; ,\] ce qui revient à : \[ \left(\hat{θ}-θ_0 \right) \stackrel{\mathrm{loi}}{\rightarrow} \mathcal{N}\left(0,\mathcal{J}^{-1}(\hat{θ})\right) \; .\] À taille d'échantillon finie, nous pourrons donc utiliser : \[ \left(\hat{θ}-θ_0 \right) \sim \mathcal{N}\left(0,\mathcal{J}^{-1}(\hat{θ})\right) \] pour construire des « ensembles de confiances » qu'on appelle dans ce cas des ensembles de Wald puisqu'ils dérivent du test de Wald.
Une autre méthode, généralement plus fiable à taille d'échantillon finie, pour construire des ensembles de confiance est la méthode du rapport de vraisemblance basée sur : \[2 \left( l(\hat{θ}) - l(θ_0) \right) \stackrel{\mathrm{loi}}{\rightarrow} χ_p^2 \; ,\] où p est la dimension de Θ.
3.6 Premier exemple simple
On considère une expérience de mesure de durée de vie de disques durs d'ordinateurs. À t=0 l'ordinateur (ou, plus vraisemblablement l'appareil de test) est mis en route jusqu'à ce que le disque tombe en panne. On peut raisonnablement supposer que les durées de vie des disques sont indépendantes et on décide de travailler (pour commencer au moins) avec un modèle simple de durée de vie exponentielle de paramètre τ. Si nous notons Di la variable aléatoire décrivant la durée de vie du ième disque on suppose donc :
\[p(D_i = d_i | τ) = (1/τ) \, \exp(-d_i/τ) \; .\]
Comme les Di sont aussi supposées IID on a pour la loi conjointe :
\[p(D_1=d_1,\ldots,D_n=d_n | τ) = \prod_{i=1}^n \left((1/τ) \, \exp(-d_i/τ) \right) \; ,\]
soit pour la log-vraisemblance :
\[l(τ | d_1,\ldots,d_n) = -n \, \log τ - \frac{\sum_{i=1}^n d_i}{τ} \; .\]
On montre alors immédiatement en annulant la fonction score que :
\[ \hat{τ} = \frac{1}{n} \sum_{i=1}^n d_i \; .\]
Ainsi l'estimateur du maximum de vraisemblance (EMV) d'une loi exponentielle est la moyenne empirique.
On montre aussi facilement que l'information observée en \(\hat{τ}\) est :
\[\mathcal{J}(\hat{τ}) = \frac{n}{\hat{τ}^2} \; ,\]
d'où :
\[ \hat{τ} - τ_0 \approx \mathcal{N}(0,\frac{\hat{τ}^2}{n}) \; .\]
Nous pouvons tester cela avec des simulations dans R :
taillesDEchantillon <- seq(10,1000,10) nombreDeRepliques <- 1000 tau.vrai <- 1 set.seed(20061001,"Mersenne-Twister") dureeDeVie <- sapply(taillesDEchantillon, function(n) { sapply(1:nombreDeRepliques, function(i) mean(rexp(n,1/tau.vrai)))})
On construit alors un graphe avec la variance empirique de l'EMV comparée à sa valeur théorique avec :
par(cex=1,5) plot(taillesDEchantillon,1/taillesDEchantillon, xlab="Taille de l'échantillon", ylab="Variance de l'estimateur", type="l",lwd=2,col="red") points(taillesDEchantillon, apply(dureeDeVie,2,var))
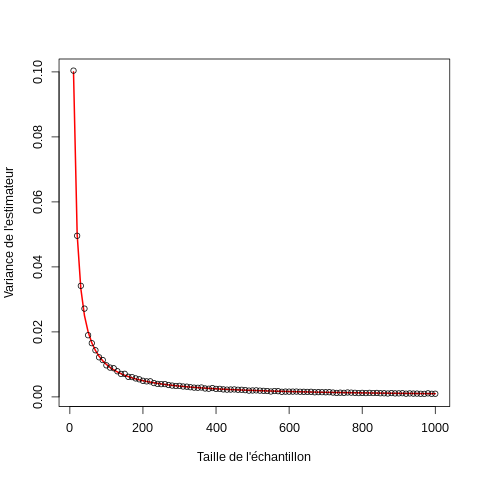
3.6.1 Propriétés empiriques de la statistique de Wald
Nous allons construire des intervalles de confiances suivant deux méthodes : celle de Wald et celle des rapports de vraisemblance, en réduisant encore la taille de l'échantillon considéré, c.-à-d. en prenant une taille de 5 au lieu de la plus petite taille de 10. Commençons donc par construire un échantillon de taille 5 :
echantillon5 <- sapply(1:nombreDeRepliques, function(i) rexp(5,1/tau.vrai))
D'après la théorie ci-dessus, si la limite asymptotique est atteinte, l'EMV de τ, c'est-à-dire dans ce cas la moyenne empirique, doit suivre une loi normale centrée sur la vraie valeur (1) avec une variance égale à \(1^2/n\), c'est-à-dire, 0.2. Nous pouvons ici construire une estimation de la densité de probabilité de \(\hat{τ}\) avec un histogramme et lui superposer la densité théorique :
par(cex=2) hist(apply(echantillon5,2,mean),breaks=50, main="",xlab=expression(hat(tau)), ylab="Densité empirique",probability=TRUE) toto <- seq(-0.5,2.5,len=501) lines(toto,dnorm(toto,1,sqrt(0.2)),col=2,lwd=2)
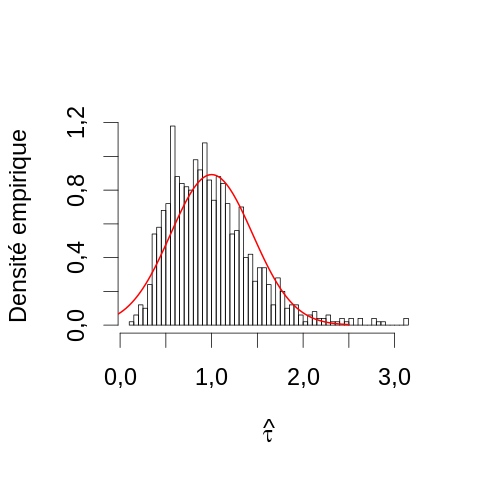
On voit ici deux problèmes :
- la « théorie » prise au pieds de la lettre nous prévoit des valeurs possibles de \(\hat{τ}\) que nous savons être impossibles car négatives (puisque l'EMV est par définition dans ce cas une moyenne empirique d'observations strictement positives) ;
- la densité empirique (l'histogramme) est bien plus asymétrique que ne le prévoit la loi asymptotique, le mode (pic) est un peu à gauche de 1 et d'assez grandes déviations positives sont observées.
Une façon plus quantitative de vérifier l'adéquation entre un histogramme – construit avec une taille de bin suffisamment petite – est une densité théorique est le hanging rootogram. L'idée est la suivante : soit \(p_i\) la probabilité d'observer un événement dans le bin i – théoriquement on a \(p_i = \int_{g_i}^{d_i} f(x) \, dx\), où f est la densité théorique et où le bin i est défini comme l'intervalle \([g_i,d_i]\) et soit n le nombre total d'observations IIDs effectuées. Le nombre d'observations dans le bin i devrait suivre, si la théorie est exacte, une loi binomiale de paramètres \(p_i\) et n (c'est-à-dire avoir une espérance de \(n \, p_i\) et une variance \(n \, p_i \, (1-p_i)\)). Maintenant si \(n\) devient très grand et si \(p_i\) devient très petit avec un produit \(λ_i \equiv n \, p_i\) constant, la loi binomiale tend vers une loi de Poisson de paramètre \(λ_i\). Si nos hypothèses sur f (ici une loi normale centré sur 1 de variance 0.2) sont correctes nos comptes par bin devraient suivre approximativement une loi de Poisson. Cela implique que si le bin est dans une région où f est grande l'amplitude des écarts entre prédiction théorique et observations devraient être typiquement plus grands que si le bin est dans une région où f est petite (puisque que la variance d'une variable aléatoire de Poisson est égale à sa moyenne) cela signifie que nous ne devrions pas avoir des écarts homogènes entre densité empirique (histogramme) et densité théorique; dit autrement, juger à l'œil l'écart entre la courbe rouge et l'histogramme de la figure précédente pourrait nous induire en erreur. Pour rendre une telle comparaison plus objective, nous allons chercher une transformation de nos observations qui stabilise leur variance. Pour ce faire nous partons de la convergence en loi d'une loi de Poisson paramètre \(λ_i\) vers une loi normale d'espérance et de variance \(λ_i\) – ça se monte bien avec les fonctions caractéristiques, les transformées de Fourier, pour vous en convaincre, faites quelques figures avec \(λ_i \ge 25\). Si nous notons \(B_i\) la variable aléatoire modélisant notre nombre d'observations dans le bin i nous avons approximativement : \[ B_i \sim \mathcal{N}(λ_i,λ_i) \] et nous pouvons écrire pour chacune de nos observations : \[ b_i = λ_i + \sqrt{λ_i} \, ε_i \] où \(ε_i\) est la réalisation d'une variable aléatoire normale centrée réduite (de moyenne 0 et de variance 1). Si nous définissons une nouvelle variable aléatoire \(Z_i \equiv g(B_i)\), où g est une fonction inversible (on peut démontrer ce qui suit avec des conditions moins restrictives sur g) on a alors : \[ z_i \approx g(λ_i) + \sqrt{λ_i} \, g'(λ_i) \, ε_i \; .\] Dit autrement, \(Z_i\) est approximativement normale de moyenne \(g(λ_i)\) et de variance \(λ_i \, g'(λ_i)^2\) (en Physique vous appelez ça la propagation des incertitudes ou des erreurs, en Stats cela s'appelle la méthode delta). Ici il nous reste à trouver g telle que \(\sqrt{x} \, g'(x) = Cste\) soit \(g'(x) α 1/\sqrt{x}\). On voit donc que \(g(x) \equiv \sqrt{x}\) fait ce qu'on veut. Ainsi, avec \(Z_i = \sqrt{B_i}\) on a : \[ z_i \approx \sqrt{λ_i} + 1/2 \, ε_i \] et \(Z_i\) est approximativement normale de moyenne \(\sqrt{λ_i}\) et de variance 1/4. On pourra s'en convaincre facilement avec une petite simulation :
λV <- c(25,50,100,500,1000) rbind(λV, sapply(λV, function(λ) var(sqrt(rpois(10000,λ)))))
| 25 | 50 | 100 | 500 | 1000 |
| 0.248511073137574 | 0.254422562155565 | 0.249791185332671 | 0.249296479745432 | 0.250690072359889 |
Pour faire notre test visuel nous prenons la racine des comptes par bin et nous soustrayons la racine carrée de la densité théorique multipliée par la taille du bin et par le nombre total d'événements dans l'échantillon. Nous pouvons rajouter au graphe des lignes horizontales correspondant à plus ou moins 2 fois l'écart type théorique (0.5) :
par(cex=2) mesBornes <- seq(0,3.5,0.1) histTaille5 <- hist(apply(echantillon5,2,mean), breaks=mesBornes,plot=FALSE) theoTaille5 <- diff(pnorm(histTaille5$breaks,1,sqrt(0.2)))*dim(echantillon5)[2] plot(histTaille5$mids, sqrt(histTaille5$counts)-sqrt(theoTaille5), type="l",lwd=2, main="",xlab=expression(hat(tau)), ylab="") abline(h=c(-1,1),col=2,lty=2) abline(h=0,col="grey80")
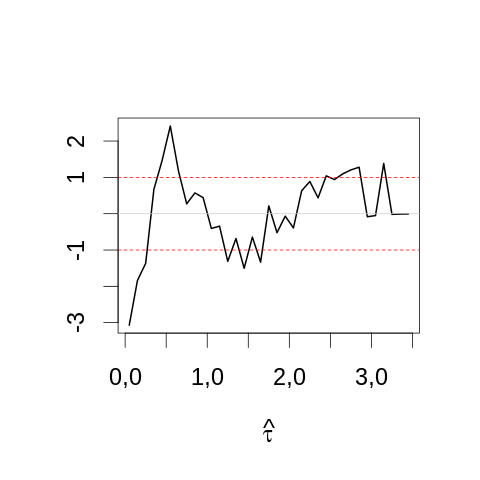
On peut comparer au même graphe construit avec la plus grande taille d'échantillon simulé (1000) :
par(cex=2) σ <- sqrt(1/1000) mesBornes <- seq(-5,5,0.2)*σ+1 histTaille1000 <- hist(dureeDeVie[,100], breaks=mesBornes,plot=FALSE) theoTaille1000 <- diff(pnorm(histTaille1000$breaks,1,σ))*dim(dureeDeVie)[1] plot(histTaille1000$mids, sqrt(histTaille1000$counts)-sqrt(theoTaille1000), type="l",lwd=2, main="",xlab=expression(hat(tau)), ylab="",ylim=range(sqrt(histTaille5$counts)-sqrt(theoTaille5))) abline(h=c(-1,1),col=2,lty=2) abline(h=0,col="grey80")
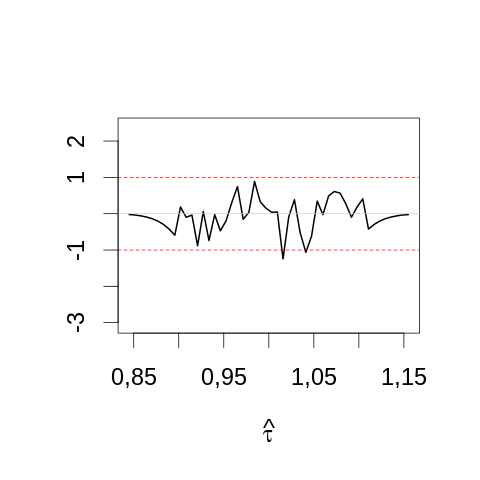
3.6.2 Hanging rootogram pour la statistique du rapport de vraisemblance
Nous venons de construire des hanging rootograms pour la statistique de Wald comparée à sa loi asymptotique avec deux tailles d'échantillons : 5 et 1000. On a vu clairement qu'avec la plus petite taille d'échantillon, la limite asymptotique n'a pas été atteinte. Nous pouvons répéter l'opération avec une autre statistique, celle du rapport de vraisemblance. Pour la cas qui nous occupe, comme l'EMV, \(\hat{τ}\) est la moyenne empirique, on peut écrire la log-vraisemblance : \[l(τ) = -n \, \left(\log τ + \hat{τ}/τ\right)\] et la statistique du rapport de vraisemblance prend la forme – en notant τ0 la vraie valeur de τ : \[\hat{r} = - 2 \, n \, \left( \log (\hat{τ}/τ_0) + 1 - \hat{τ}/τ_0 \right) \; .\] Dans le cadre de nos simulation nous avons de plus : τ0 = 1. Il ne nous reste plus qu'à calculer la valeur de la statistique pour chaque simulation, construire une estimation de la densité (c.-à-d. un histogramme) à partir de ses valeurs, calculer la valeur de \(n \, \int_{g_i}^{d_i} χ^2_1(x) \, dx\) – ici la loi asymptotique est un χ2 à un degré de liberté – puis prendre les racines carrées avant de former la différence 1.
par(cex=2) τ.chapeau <- apply(echantillon5,2,mean) rV <- -5*(log(τ.chapeau/tau.vrai) + 1- τ.chapeau/tau.vrai)*2 yl <- range(rV) mesBornes <- seq(yl[1]-0.5,yl[2]+0.5,len=51) histTaille5 <- hist(rV, breaks=mesBornes,plot=FALSE) chi2Taille5 <- diff(pchisq(histTaille5$breaks,1))*dim(echantillon5)[2] plot(histTaille5$mids, sqrt(histTaille5$counts)-sqrt(chi2Taille5), type="l",lwd=2, main="",xlab=expression(hat(r)), ylab="") abline(h=c(-1,1),col=2,lty=2) abline(h=0,col="grey80")
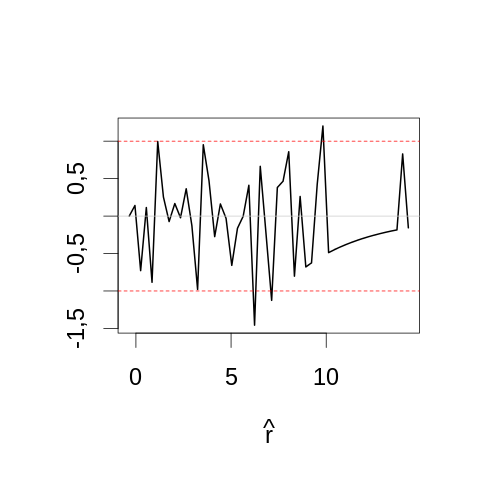
On constate que même pour une aussi petite taille d'échantillon, la statistique semble assez proche de sa valeur asymptotique. On est donc pas surpris par le comportement observé avec la plus grande taille d'échantillon (1000) :
par(cex=2) τ.chapeau <- dureeDeVie[,100] rV <- -1000*(log(τ.chapeau/tau.vrai) + 1- τ.chapeau/tau.vrai)*2 yl <- range(rV) mesBornes <- seq(yl[1]-0.1,yl[2]+0.1,len=51) histTaille1000 <- hist(rV, breaks=mesBornes,plot=FALSE) chi2Taille1000 <- diff(pchisq(histTaille1000$breaks,1))*dim(dureeDeVie)[1] plot(histTaille1000$mids, sqrt(histTaille1000$counts)-sqrt(chi2Taille1000), type="l",lwd=2, main="",xlab=expression(hat(r)), ylab="",ylim=range(sqrt(histTaille5$counts)-sqrt(chi2Taille5))) abline(h=c(-1,1),col=2,lty=2) abline(h=0,col="grey80")
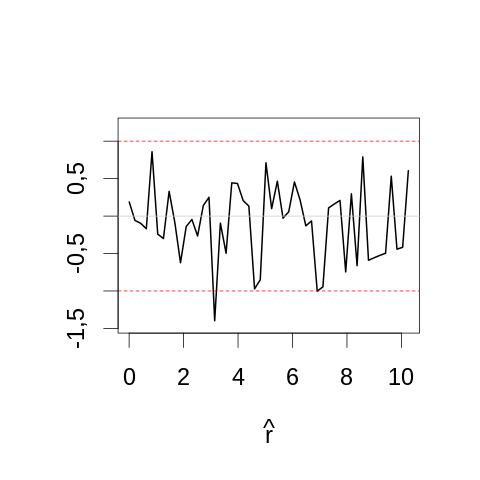
3.6.3 Étude empirique de la probabilité de recouvrement des intervalles de confiances construits avec la méthode de Wald et avec la méthode du rapport de vraisemblance
On construit immédiatement des intervalles de confiances avec la méthode de Wald : \[ [\hat{τ} + φ^{-1}\left(α/2\right) \, \sqrt{\hat{τ}/n} , \hat{τ} - φ^{-1}\left(α/2\right) \, \sqrt{\hat{τ}/n} ] \; ,\] où \(φ\) désigne la fonction de répartition d'une loi normale centrée réduite et \(φ^{-1}\) est son inverse ; α est le niveau du test. On peut donc, pour chacune de nos 1000 expériences simulées, tracer un intervalle de confiance à 95% est regarder si la vraie valeur (1) s'y trouve bien 95 fois sur 100, c'est-à-dire à peu près 950 fois sur 1000 dans notre cas. Clairement la validité des intervalles de confiance dépend de la validité de l'approximation asymptotique de la statistique utilisée. Compte tenu de ce que nous avons vu dans les deux sections précédentes, nous ne nous attendons pas à ce que les intervalles de confiance à 95% basés sur la statistique de Wald aient une probabilité de recouvrement empirique identique à leur probabilité nominale (ou théorique).
par(cex=1.5) τ.chapeau <- apply(echantillon5,2,mean) τ.IC <- τ.chapeau + qnorm(0.975) * (c(-1,1) %o% sqrt(τ.chapeau/5)) τ.vrai.dedans <- apply(τ.IC,2, function(x) x[1] <= 1 && 1 <= x[2]) plot(c(0,1000), range(τ.IC), type="n", xlab="Indice de réplique", ylab="", main="Intervalles basés sur la méthode de Wald") abline(h=1,col="orange",lwd=2) invisible(sapply(1:1000, function(i) { x <- τ.IC[,i] dedans <- τ.vrai.dedans[i] segments(i,x[1],i,x[2],col=ifelse(dedans,1,2))}))
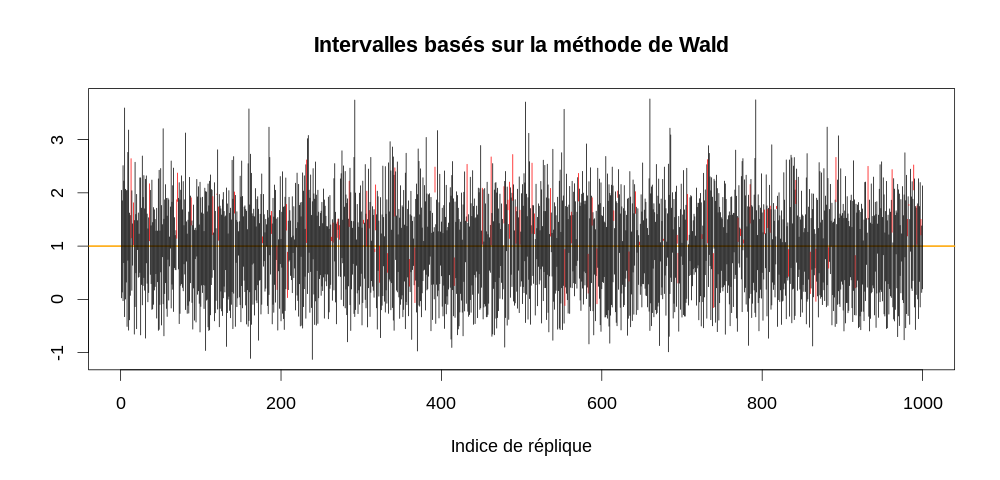
On a ici seulement :
sum(τ.vrai.dedans)
914
qui contiennent la vraie valeur.
Pour la méthode du rapport de vraisemblance, nous avons, lorsque la limite asymptotique est atteinte : \[2 \, \left( l(\hat{τ}) - l(τ_0) \right) \sim χ^2_1 \; .\] Ainsi : \[ \mathrm{Pr} \{ 2 \, \left( l(\hat{τ}) - l(τ_0) \right) \le z \} = \mathrm{pchisq}(z,1) \; ,\] où \(\mathrm{pchisq}(z,1)\) désigne la valeur de la fonction de répartition d'un loi \(χ^2_1\) en z. Nous allons donc construire un intervalle de niveau α en cherchant τg ≤ \(\hat{τ}\) ≤ τd, tels que : \[ 2 \, \left( l(\hat{τ}) - l(τ_{g,d}) \right) = \mathrm{qchisq}(1-α,1) \; \] où \(\mathrm{qchisq}(1-α,1)\) désigne la valeur de l'inverse de la fonction de répartition d'un χ21 en 1-α. Pour trouver les valeurs \(τ_{g,d}\) nous devons procéder numériquement :
q95 <- qchisq(0.95,1) τ.IC <- sapply(1:1000, function(i) { τ.emv <- τ.chapeau[i] lFct <- function(τ) -5*(log(τ) + τ.emv/τ) lAτ.chapeau <- lFct(τ.emv) cible <- function(τ) 2*(lAτ.chapeau - lFct(τ)) - q95 icBas <- uniroot(cible,c(0.001,τ.emv))$root icHaut <- uniroot(cible,c(τ.emv,100))$root c(icBas,icHaut) }) τ.vrai.dedans <- apply(τ.IC,2, function(x) x[1] <= 1 && 1 <= x[2]) plot(c(0,1000), range(τ.IC), type="n", xlab="Indice de réplique", ylab="", main="Intervalles basés sur le rapport de vraisemblance") abline(h=1,col="orange",lwd=2) invisible(sapply(1:1000, function(i) { x <- τ.IC[,i] dedans <- τ.vrai.dedans[i] segments(i,x[1],i,x[2],col=ifelse(dedans,1,2))}))
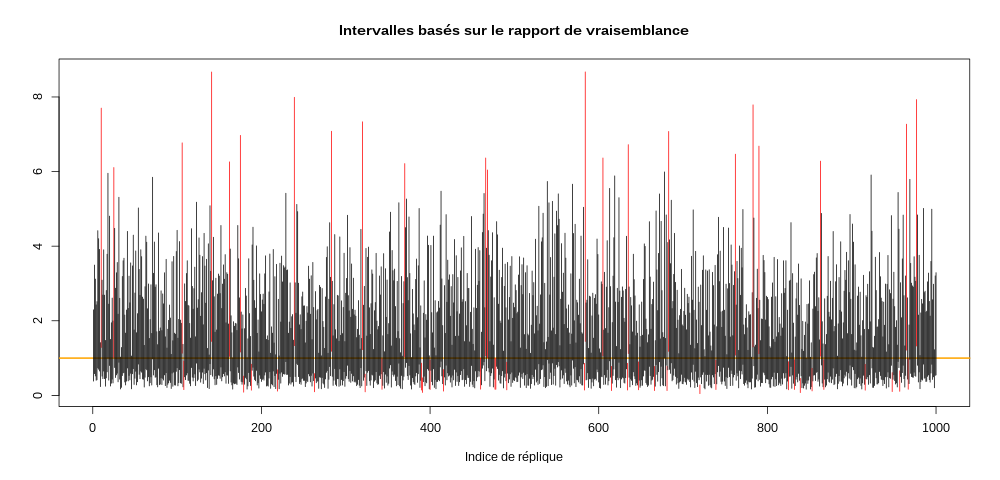
On a cette fois :
sum(τ.vrai.dedans)
946
intervalles contenant la bonne valeur…
3.7 Un deuxième exemple à peine plus compliqué
On suppose que des comptes de photons \(y_1,y_2,\ldots,y_n\) sont effectués à des temps \(t_1,t_2,\ldots,t_n\) (\(0 ≤ t_1 < t_2 < \cdots < t_n\)) et que la loi suivie par l'observation i est une loi de Poisson de paramètre : \(λ_i = a + δ \, \exp(-t_i / τ)\). On suppose de plus que les yi constituent des observations statistiquement indépendantes. Leur loi conjointe s'écrit alors :
\[\mathrm{Pr}\left(Y_1=y_1,\ldots,Y_n=y_n|t_1,\ldots,t_n,a,δ,τ\right) = \prod_{i=1}^n \left( \frac{λ_i^{n_i}}{n_i !} \, \exp(-λ_i) \right) \; .\]
D'où la log-vraisemblance :
\[l(a,δ,τ) = \sum_{i=1}^n \left( n_i \, \log λ_i - λ_i \right) \; .\]
Pour faire simple nous allons supposer que a = 50 et δ = 500 et sont connus et que trois observations sont faites à t1 = 0, t2 = 4 et t3 = 10. La vraie valeur de τ est 5 et nous allons utiliser R pour simuler des données et obtenir l'EMV que nous comparerons à l'estimateur des moindres carrés :
a.vrai <- 50 delta.vrai <- 500 tau.vrai <- 5 temps <- c(0,4,10) lambdaFct <- function(t,a=a.vrai,delta=delta.vrai,tau=tau.vrai) a + delta * exp(-t/tau) faitLV <- function(observations, tV=temps, a=a.vrai, delta=delta.vrai) { function(tau) { ideal <- lambdaFct(tV,a,delta,tau) sum(observations*log(ideal)-ideal) } } faitSRC <- function(observations, tV=temps, a=a.vrai, delta=delta.vrai) { function(tau) { ideal <- lambdaFct(tV,a,delta,tau) sum((observations-ideal)^2) } } set.seed(20110928) test1 <- sapply(1:10000, function(i) { obs <- rpois(length(temps),lambdaFct(temps)) f1 <- faitLV(obs) f2 <- faitSRC(obs) c(optimize(f1,c(0,10),maximum=TRUE)$maximum, optimize(f2,c(0,10))$minimum) }) rbind(apply(test1,1,mean), apply(test1,1,var))
| 4.9994055911246 | 4.99987988968659 |
| 0.0927442947356498 | 0.108922749758736 |
3.8 Retour sur les données de fertilité de la communauté Hutterite considérées par Ihaka
3.8.1 Question
Nous considérons les données de fertilité de la communauté Huttérite étudiées par R. Ihaka dans son 4e cours. En nous basant sur l'analyse d'Ihaka, nous « adoptons comme vraie » la fonction de répartition du temps (en mois) entre marriage et première grossesse suivante : \[F(t) = 1 - \frac{h^a}{(h+t)^a} \quad \textrm{avec} \quad a \, = \, 3,1 \quad \textrm{et} \quad h \, = \, 9,6 \; . \]
L'échantillon considéré par Ihaka comprend 342 femmes. Les temps entre mariage et grossesse avaient de plus été tabulé suivant une partition dont les limites étaient :
(breaks <- c(0:12,15,18,24,Inf))
[1] 0 1 2 3 4 5 6 7 8 9 10 11 12 15 18 24 Inf
Pour mémoire, les données sont :
| mois | nombre |
|---|---|
| 0-1 | 103 |
| 1-2 | 53 |
| 2-3 | 43 |
| 3-4 | 27 |
| 4-5 | 30 |
| 5-6 | 9 |
| 6-7 | 12 |
| 7-8 | 9 |
| 8-9 | 6 |
| 9-10 | 8 |
| 10-11 | 10 |
| 11-12 | 5 |
| 12-15 | 9 |
| 15-18 | 7 |
| 18-24 | 7 |
| 24+ | 4 |
Nous allons supposer que nous disposons de données non discrétisées et nous souhaitons comparer les performances de trois estimateurs du couple (a,h) de paramètres du modèles :
- l'estimateur du maximum de vraisemblance appliqué aux données brutes ;
- l'estimateur du maximum de vraisemblance appliqué aux données tabulées selon la même partition que les données originale ;
- l'estimateur du moindre χ2, c'est-à-dire celui utilisé par Ihaka.
Nous allons faire cette étude par simulation, c'est-à-dire que nous allons simuler, disons 1000 fois, une échantillon de 342 variables IID dont la fonction de répartition est donnée par notre première équation. Pour chacun de nos 1000 échantillons, nous obtiendrons 3 estimations du couple (a,b) de paramètres et nous comparerons nos estimations en construisant leurs histogrammes.
3.8.2 Génération des échantillons par ma méthode de la transformée inverse
La Méthode de la transformée inverse, toujours applicable mais souvent coûteuse consiste en générer un nombre, U, suivant une loi uniforme sur [0,1] avant de trouver X tel que F(X) = U, où F est la fonction de répartition de la loi cible. X a alors F pour fonction de répartition. On prouve cela facilement lorsque F est strictement croissante, on a en effet : \[X \sim \mathrm{F}^{-1}(U)\, , \quad \mathrm{où} \quad U \sim \mathcal{U}(0,1) \; .\] Par définition: \[\mathrm{F}_X(x) \equiv \mathrm{Pr}\{X \le x\} \; ,\] mais \[\begin{array}{l l l} \mathrm{Pr}\{X \le x\} & = & \mathrm{Pr}\{\mathrm{F}(X) \le \mathrm{F}(x)\} \quad \mathrm{(F} \; \textrm{strictement croissante)} \\ \mathrm{Pr}\{X \le x\} & = & \mathrm{Pr}\{U \le \mathrm{F}(x)\} \quad \textrm{(définition de} \; X \mathrm{)} \\ \mathrm{Pr}\{X \le x\} & = & \mathrm{F}(x) \quad \textrm{(car} \; U \; \textrm{est uniforme sur} \; [0,1) \textrm{)} \\ \mathrm{F}_X(x) & = & \mathrm{F}(x) \; . \end{array}\]
La mise en oeuvre « brutale » de cette méthode est numérique et utilise la recherche de la racine de la fonction U-F(X), avec uniroot dans R. On pourrait ainsi générer n observations suivant notre loi avec la fonction :
rHutterite <- function(n) sapply(runif(n), function(u) uniroot(function(x) u-1+1/(1+x/9.6)^3.1,c(0,100))$root)
Une façon plus élégante et plus efficace de faire la même chose et d'inverser analytiquement notre fonction de répartition. Nous avons en effet : \[\begin{array}{l l l} F(t) & = & 1 - \frac{h^a}{(h+t)^a} \\ F(t) & = & 1 - \frac{1}{(1+t/h)^a} \\ 1 - F(t) & = & \frac{1}{(1+t/h)^a} \\ \frac{1}{1 - F(t)} & = & (1+t/h)^a \\ \frac{1}{\sqrt[a]{1 - F(t)}} & = & (1+t/h) \\ \frac{h}{\sqrt[a]{1 - F(t)}} - h & = & t \end{array}\]
Nous pouvons ainsi définir une suite de fonctions liées à la loi qui nous intéresse en suivant les conventions (implicites) de R :
dHutterite <- function(x, a=3.1, h=9.6) a/h/(1+x/h)^(a+1) pHutterite <- function(q, a=3.1, h=9.6) 1-1/(1+q/h)^a qHutterite <- function(p, a=3.1, h=9.6) h*((1-p)^(-1/a)-1) rHutterite <- function(n, a=3.1, h=9.6) qHutterite(runif(n),a,h)
On vérifie facilement que de grosses erreurs n'ont pas été commises dans nos définitions de la fonction de répartition (pHutterite) et de la fonction quantile (qHutterite) avec :
pp <- seq(0,1,len=101)
max(abs(pHutterite(qHutterite(pp))-pp))
2.98372437868011e-16
3.8.3 Définitions des fonctions à optimiser
3.8.3.1 Cas du maximum de vraisemblance sur les données brutes
La densité de probabilité de l'intervalle entre mariage et première grossesse et directement obtenue en dérivant la fonction de répartition : \[f(t) = \frac{dF(t)}{dt} = \frac{a}{h \, (1 + t/h)^{a+1}} \; .\] La densité conjointe d'un échantillon {T1,\(\ldots\),TN} est donc (sous l'hypothèse IID) : \[f(T_{1},\ldots,T_{N}) = \prod_{i=1}^{N} \frac{a}{h \, (1 + T_{i}/h)^{a+1}} \; .\] La fonction de log-vraisemblance est donc : \[\mathcal{l}\left(θ = (a,h)\right) = N \, (\log a - \log h) - (a+1) \, \sum_{i=1}^{N} \log (1 + T_{i}/h) \; .\]
Si nous appelons obs notre vecteur d'observations, nous pouvons définir notre fonction à optimiser (l'opposée de la log-vraisemblance) par :
moinsLogVraiBrute <- function(θ,obs) { N <- length(obs) a <- θ[1] h <- θ[2] N*(log(h)-log(a)) + (a+1)*sum(log(1+obs/h))}
3.8.3.2 Cas du maximum de vraisemblance sur les données tabulées
Ici c'est à la limite plus simple, une fois que des valeurs de a et h sont disponibles, on peut directement, en suivant le développement d'Ihaka obtenir la probabilité d'une observation dans chacune des classes de la partitions, on est alors dans le cadre d'une loi multinomiale, c'est-à-dire que le modèle nous permet de calculer un vecteur P=(p1,\(\ldots\),pk) et la probabilité, étant donné que N individus ont été observés, dans avoir n1 dans la première classe, \(\ldots\), nk dans la k-ième est : \[\mathrm{Pr}\{N_{1}=n_{1},\ldots,N_{k}=n_{k}\} = \frac{N!}{n_{1}!\cdots n_{k}!} p_{1}^{n_{1}} \cdots p_{k}^{n_{k}} \; .\] Ici, pour faire court, j'écris pi ce que je devrais écrire pi(a,h). Lorsque nous définissons notre vraisemblance, nous pouvons « oublier » le pré-facteur avec les factoriels puisqu'il ne dépend pas des paramètres — il n'influence donc pas la position du maximum, seulement la valeur au maximum —, ce qui nous donne la log-vraisemblance suivante : \[\mathcal{l}\left(θ = (a,h)\right) = \sum_{i=1}^{k} n_{i} \, \log p_{i}(a,h) \; .\] Notre fonction à optimiser devient :
moinsLogVraiTab <- function(θ,obs,b=breaks) { a <- θ[1] h <- θ[2] y <- hist(obs,breaks=b,plot=FALSE)$counts F <- 1-1/(1+breaks/h)^a p <- diff(F) -sum(y*log(p))}
3.8.3.3 Cas de la minimisation du χ2 sur les données tabulées
Il suffit ici de reproduire ce que fait Ihaka sur le jeu de données simulées :
chi2Tab <- function(θ,obs,b=breaks) { a <- θ[1] h <- θ[2] N <- length(obs) y <- hist(obs,breaks=b,plot=FALSE)$counts F <- 1-1/(1+breaks/h)^a p <- diff(F)*N sum((y-p)^2/p)}
3.8.4 Simulations
Nous avons désormais tout ce qu'il nous faut pour répondre à notre question. Un truc à utiliser pour gagner du temps et de commencer nos optimisations avec la vraie valeur des paramètre du modèle :
nrep <- 1000 set.seed(20061001,"Mersenne-Twister") N <- 342 sim <- sapply(1:nrep, function(i) { obs <- rHutterite(N) fit1 <- optim(log(c(3.1,9.6)),function(p) moinsLogVraiBrute(exp(p),obs),method="BFGS") fit2 <- optim(log(c(3.1,9.6)),function(p) moinsLogVraiTab(exp(p),obs),method="BFGS") fit3 <- optim(log(c(3.1,9.6)),function(p) chi2Tab(exp(p),obs),method="BFGS") c(fit1conv = fit1$convergence, fit1a = fit1$par[1], fit1h = fit1$par[2], fit2conv = fit2$convergence, fit2a = fit2$par[1], fit2h = fit2$par[2], fit3conv = fit3$convergence, fit3a = fit3$par[1], fit3h = fit3$par[2]) } ) c(sum(sim[1,] > 0),sum(sim[4,] > 0),sum(sim[7,] > 0))
| 0 |
| 0 |
| 0 |
4 Quelques exercices
4.1 Une épidémie de rougeole : le sujet d'examen de juin 2011
L'un des enfants d'une famille de trois enfants rentre à la maison avec la rougeole. Chacun des deux autres enfants de la famille peut être infecté par le premier enfant avec une probabilité θ. Si aucun des deux autres enfants ou si les deux autres enfants attrapent la rougeole, l'épidémie s'arrête. Par contre, si un des deux autres attrape la rougeole, il peut la transmettre au troisième avec la même probabilité θ.
4.1.1 Question 1
Soit N le nombre total d'enfants de la famille (de trois enfants) infectés avant la fin de l'épidémie. Montrez que : \[ \mathrm{Pr}\left(N=1\right) = (1-\theta)^2 \; ; \quad \mathrm{Pr}\left(N=2\right) = 2\, \theta \, (1-\theta)^2 \; ; \quad \mathrm{Pr}\left(N=3\right) = \theta^2 \, (3-2\,\theta) \; ; \] Vous supposerez que les infections ont lieu indépendamment et vous pourrez vous rappeler que la somme des probabilités de tous les cas possibles doit être égale à 1.
4.1.2 Réponse 1
- La probabilité pour qu'aucun des deux autres enfants ne soit infecté est, du fait de l'indépendance, le produit des probabilités pour qu'ils ne le soient pas individuellement d'où : \(\mathrm{Pr}\left(N=1\right) = (1-\theta)^2\) ;
- Pour qu'un seul enfant soit infecté il faut qu'il soit infecté (probabilité θ) et que l'autre ne le soit ni par le premier enfant (probabilité 1-θ) ni par celui nouvellement infecté (probabilité 1-θ), d'où la probabilité pour que un enfant donné soit infecté alors que l'autre ne l'est pas: \(\theta \, (1-\theta)^2\) et comme il y a deux enfants, la probabilité pour qu'on est au total 2 enfants infectés : \(2 \, \theta \, (1-\theta)^2\) ;
- on doit avoir : \(\mathrm{Pr}\left(N=1\right) + \mathrm{Pr}\left(N=2\right) + \mathrm{Pr}\left(N=3\right) = 1\), soit \(\mathrm{Pr}\left(N=3\right) = 1 - \mathrm{Pr}\left(N=1\right) - \mathrm{Pr}\left(N=2\right)\), \(\mathrm{Pr}\left(N=3\right) = 1 - (1-\theta)^2 - 2 \, \theta \, (1-\theta)^2\). En développant le deuxième terme du second membre on obtient : \(\mathrm{Pr}\left(N=3\right) = 2\, \theta-\theta^2 - 2 \, \theta \, (1-\theta)^2\), en développant tout il vient : \(\mathrm{Pr}\left(N=3\right) = 2\, \theta-\theta^2 - 2 \, \theta + 4 \, \theta^2 - 2 \, \theta^3\) et en simplifiant : \(\mathrm{Pr}\left(N=3\right) = \theta^2 \, (3-2\,\theta)\).
4.1.3 Question 2
Vous écrirez les expressions de la log-vraisemblance, de la fonction score et de la fonction d'information observée lorsqu'un échantillon de K familles de trois enfants est observé et que k1 familles restent avec un seul enfant infecté, k2 familles en ont deux et k3 familles en ont trois. Les familles sont bien sûr supposées indépendantes (au sens statistique du terme). Inutile de vous « alourdir » avec des termes ne faisant pas intervenir le paramètre θ.
4.1.4 Réponse 2
En supposant l'indépendance des familles on a : \[\mathrm{Pr}\left(K_1=k_1,K_2=k_2,K_3=k_3 | \theta \right) = C \, \mathrm{Pr}\left(N=1\right)^{k_1} \, \mathrm{Pr}\left(N=2\right)^{k_2} \, \mathrm{Pr}\left(N=3\right)^{k_3} \; ,\] où C est une constante de normalisation ne dépendant que de K, k1, k2 et k3 – on a ici affaire à une loi multinomiale et \(C=K!/(k_1 ! \, k_2 ! \, k_3 !)\).
La log vraisemblance devient : \[l(\theta) = 2 \, (k_1 + k_2) \, \log (1-\theta) + (k_2 + 2 \, k_3) \, \log \theta + k_3 \, \log (3-2 \, \theta ) \; .\]
La fonction score : \[ S(\theta) = - \frac{2 \, (k_1 + k_2)}{1 - \theta} + \frac{k_2+2\, k_3}{\theta} - \frac{2 \, k_3}{3 - 2\, \theta} \; .\]
L'information observée : \[\mathcal{J}(\theta) = \frac{2 \, (k_1 + k_2)}{(1 - \theta)^2} + \frac{k_2+2\, k_3}{\theta^2} + \frac{4 \, k_3}{(3 - 2\, \theta)^2} \; .\]
On voit que comme 0 ≤ k1, k2 et k3 ≤ K et k1 + k2 + k3 = K, l'information observée est toujours positive, ce qui implique que \(l(\theta)\) est concave ce qui veut dire que nous n'aurons pas de problème de convergence des méthodes d'optimisation numérique.
4.1.5 Complément 2
Par curiosité, je donne les commandes permettant d'effectuer ces petits calculs avec le logiciel Maxima (les commandes seraient très proches avec Mapple).
Définition de la log vraisemblance:
2*(k1+k2)*log(1-θ) + (k2+2*k3)*log(θ)+k3*log(3-2*θ)
print(<<log-vraisemblance()>>);
(2 k3 + k2) log(θ) + 2 (k2 + k1) log(1 - θ) + k3 log(3 - 2 θ)
La fonction score est alors simplement obtenue :
diff(2*(k1+k2)*log(1-θ)+(k2+2*k3)*log(θ)+k3*log(3-2*θ),θ,1);
diff(<<log-vraisemblance()>>,θ,1)
display2d:false;print(<<score>>);
(2*k3+k2)/θ-2*(k2+k1)/(1-θ)-2*k3/(3-2*θ)
De même que la fonction d'information observée:
-diff(2*(k1+k2)*log(1-θ)+(k2+2*k3)*log(θ)+k3*log(3-2*θ),θ,2);
-diff(<<log-vraisemblance()>>,θ,2)
display2d:false;print(<<information-observée>>);
(2*k3+k2)/θ^2+2*(k2+k1)/(1-θ)^2+4*k3/(3-2*θ)^2
4.1.6 Question 3
Une étude portant sur K = 100 familles de trois enfants donne les résultats suivants :
| nb d'enfants avec la rougeole | 1 | 2 | 3 |
| nb de familles | 48 | 32 | 20 |
Vous construirez une fonction R renvoyant la log-vraisemblance pour ce jeu de données.
4.1.7 Réponse 3
Je procède comme à mon habitude en deux temps en définissant d'abord une fonction qui construit la fonction de log-vraisemblance2 :
faitFLV <- function(k1=48,k2=32,k3=20) function(θ) 2*(k1+k2)*log(1-θ) + (k2+2*k3)*log(θ) + k3 * log(3-2*θ)
Puis je construis la fonction de log vraisemblance :
FLVvraie <- faitFLV(k1=48,k2=32,k3=20)
Vous pouvez aussi définir FLVvraie de la façon suivante:
FLVvraie <- function(θ,k1=48,k2=32,k3=20) 2*(k1+k2)*log(1-θ) + (k2+2*k3)*log(θ) + k3 * log(3-2*θ)
4.1.8 Question 4
Comme il est plutôt difficile de trouver la bonne racine de la fonction score analytiquement (avec maxima c'est faisable), nous allons le faire numériquement avec optimise. Comme cette dernière fonction demande à son utilisateur de fournir des bornes encadrant l'optimum, nous allons commencer par tracer un graphe de la log vraisemblance sur le domaine de définition de θ : (0,1) pour trouver une limite raisonnable au domaine fourni à optimise. Vous prendrez soin de mettre des labels à vos axes. Vous pourrez néanmoins regarder de près votre information observée et commenter sur la nécessité de définir un domaine « raisonnable » plus court que (0,1).
4.1.9 Réponse 4
Le code suivant nous donne directement la figure (\ref{fig:Stat2013reponse4}) demandée. (J'ai ajusté la taille des labels, par(cex=2) pour que la figure soit plus lisible ; je ne vous demandais pas de le faire dans vos fichiers de script. J'ai aussi utilisé des commandes un peu sophistiquées pour avoir des labels avec des lettres grecs, ce que je ne vous demandais pas de faire non plus.)
θθ <- seq(0,1,len=501) par(cex=2) plot(θθ, FLVvraie(θθ), type="l",lwd=3, xlab=expression(theta), ylab=expression(l(theta)))
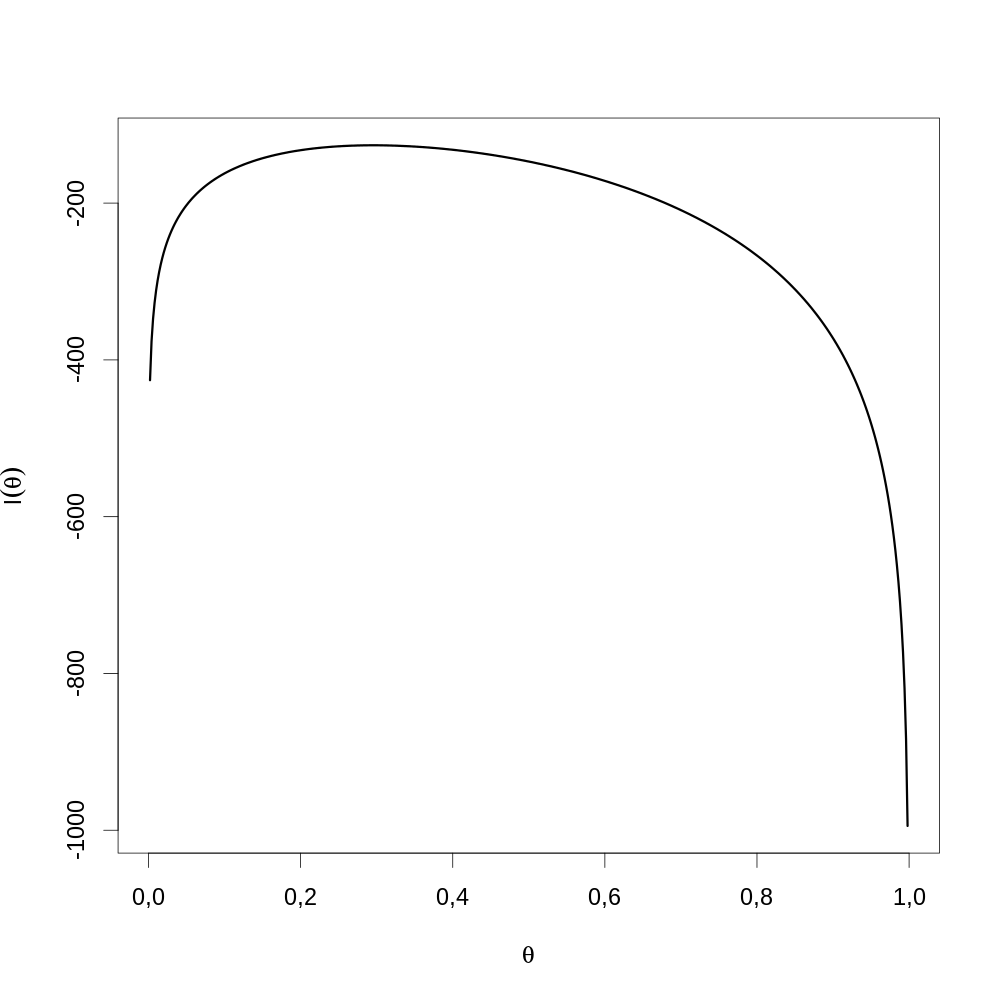
Figure 17 : Graphe de la fonction de vraisemblance sur l'ensemble du domaine de définition de θ. Comme discuté lors de la dérivation de l'information observée, la fonction est bien concave. On voit ici que le maximum est inclus dans l'intervalle [0,2;0,4]. Néanmoins comme le graphe est concave nous pourrions directement lancer optimise avec 0 et 1 comme bornes.
4.1.10 Complément 4
Comme mentionné dans l'énonce de la question, maxima nous permet d'obtenir analytiquement les racines de la fonction score:
solve(diff(2*(k1+k2)*log(1-θ)+(k2+2*k3)*log(θ)+k3*log(3-2*θ),θ,1),θ);
solve(diff(<<log-vraisemblance()>>,θ,1),θ)
display2d:false;print(<<racines-de-score>>);
[θ = -(sqrt((48*k2+48*k1)*k3+49*k2^2+84*k1*k2+36*k1^2)-12*k3-11*k2-6*k1) /(12*k3+12*k2+8*k1), θ = (sqrt((48*k2+48*k1)*k3+49*k2^2+84*k1*k2+36*k1^2)+12*k3+11*k2+6*k1) /(12*k3+12*k2+8*k1)]
Nous pouvons directement utiliser ces expression pour construire une fonction R
racineScore <- function(k1=48,k2=32,k3=20) c(-(sqrt((48*k2+48*k1)*k3+ 49*k2^2+ 84*k1*k2+ 36*k1^2)- 12*k3- 11*k2- 6*k1)/(12*k3+12*k2+8*k1), (sqrt((48*k2+48*k1)*k3+ 49*k2^2+ 84*k1*k2+ 36*k1^2)+ 12*k3+ 11*k2+ 6*k1)/(12*k3+12*k2+8*k1))
4.1.11 Question 5
Vous trouverez la valeur de votre estimateur du maximum de vraisemblance numériquement (avec, par exemple, optimise).
4.1.12 Réponse 5
(θ.chapeau <- optimize(FLVvraie,lower=0.2, upper=0.4,maximum=TRUE)$maximum)
[1] 0,2954604
4.1.13 Complément 5
Les expressions analytiques des racines de la fonction score nous donnent :
racineScore(k1=48,k2=32,k3=20)
[1] 0,2954474 1,4505843
4.1.14 Question 6
Vous préparerez un nouveau graphe avec la log vraisemblance en trait continu noir, le point maximum figuré par un disque rouge (par exemple) et son abscisse figurée par une ligne verticale pointillée. Vous êtes invités à faire un choix « judicieux » d'échelle pour vos abscisses et vos ordonnées.
4.1.15 Réponse 6
Là encore, la courte séquence de commandes suivante génère la figure demandée (\ref{fig:Stat2013reponse6}).
par(cex=2) plot(θθ, FLVvraie(θθ), type="l",lwd=3, xlab=expression(theta), ylab=expression(l(theta)), xlim=c(0.2,0.4), ylim=c(FLVvraie(0.2),FLVvraie(θ.chapeau))) abline(v=θ.chapeau,col="red",lty=3) points(θ.chapeau,FLVvraie(θ.chapeau),col="red",pch=16)
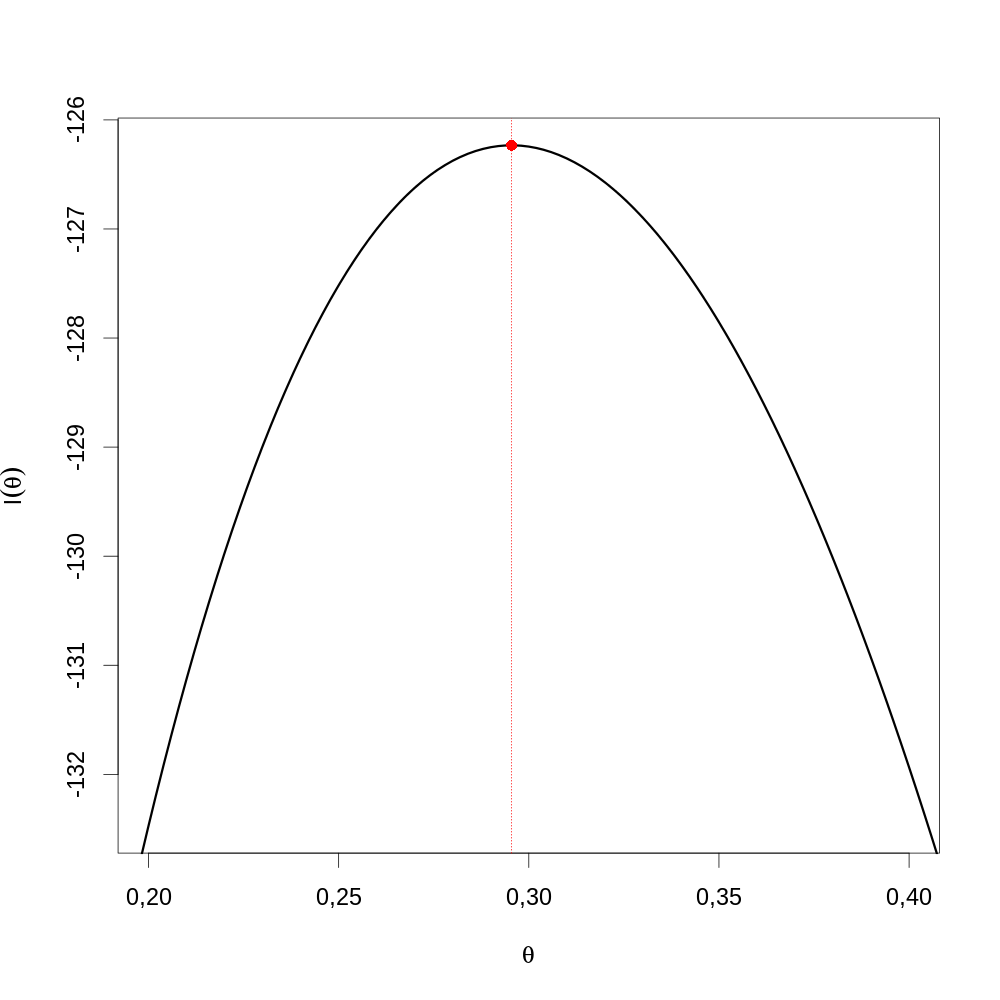
Figure 18 : Graphe de la fonction de vraisemblance (ligne noire) sur une partie sélectionnée du domaine de définition de θ autour de \(\hat{\theta}\) (droite verticale pointillée rouge).
4.1.16 Question 7
Vous utiliserez votre expression de l'information observée que vous combinerez avec votre estimateur \(\hat{\theta}\) de θ pour obtenir un intervalle de confiance à 95% avec la méthode de Wald.
4.1.17 Réponse 7
Je commence par définir une fonction qui renvoie une fonction qui renvoie l'information observée
faitInfObsF <- function(k1=48,k2=32,k3=20) function(θ) 2*(k1+k2)/(1-θ)^2 + (k2+2*k3)/θ^2 + 4*k3/(3-2*θ)^2
Puis j'appelle cette fonction pour obtenir ma fonction d'information observée :
InfObsFvraie <- faitInfObsF(k1=48,k2=32,k3=20)
La valeur de l'information observée au maximum de vraisemblance est donc :
(J.en.θ.chapeau <- InfObsFvraie(θ.chapeau))
[1] 1160,893
D'où l'erreur type sur \(\hat{\theta}\) (la racine carrée de l'inverse de l'information observée au maximum de vraisemblance) :
(σ.θ.chapeau <- 1/sqrt(J.en.θ.chapeau))
[1] 0,02934972
L'intervalle de confiance à 95% avec la méthode de Wald est donc :
θ.chapeau + c(-1,1)*qnorm(0.975)*σ.θ.chapeau
[1] 0,2379360 0,3529848
4.1.18 Question 8
Vous simulerez 1000 ou 10000 répliques de l'expérience ci-dessus en utilisant pour θ, dans les formules donnant les probabilités d'observer un, deux ou trois enfants malades, le \(\hat{\theta}\) que vous venez d'obtenir. Vous utiliserez la fonction rmultinom de R pour vos simulations; vous commencerez par lire la documentation associée et vous verrez que dans votre cas, l'argument prob doit être un vecteur de trois éléments : les probabilités d'avoir 1, 2 ou 3 enfants malades. Vous n'oublierez pas de spécifier la graine de votre générateur de nombres (pseudo)aléatoires.
4.1.19 Réponse 8
Je commence par définir une fonction de θ qui renvoie le vecteur de probabilité :
faitVecProb <- function(θ) c(un=(1-θ)^2, deux=2*θ*(1-θ)^2, trois=θ^2*(3-2*θ))
Je vérifie que les éléments du vecteur se somment à 1 :
sum(faitVecProb(θ.chapeau))
1
Je fais la simulation :
set.seed(20061001) n.rep <- 10000 nb.familles <- 100 sim.exp <- rmultinom(n.rep, nb.familles, prob=faitVecProb(θ.chapeau))
4.1.20 Question 9
Pour chacune des expériences simulées vous obtiendrez l'estimateur du maximum de vraisemblance comme vous l'avez fait avec les vraies données, vous construirez alors un histogramme (avec entre 50 et 100 bins) des \(\hat{\theta}\) auquel vous superposerez la loi asymptotique (loi normale centrée sur la vraie valeur dont la variance est l'inverse de l'information de Fisher ; pour avoir l'info de Fisher vous remplacez dans l'info observée les k1, k2, k3 par leur valeur théorique).
4.1.21 Réponse 9
Je commence par obtenir l'estimateur du maximum de vraisemblance pour chaque réplique :
θ.chapeau.sim <- apply(sim.exp,2, function(K) { FLV <- faitFLV(k1=K[1],k2=K[2],k3=K[3]) optimize(FLV,lower=0, upper=1, maximum=TRUE)$maximum })
J'obtiens l'information de Fisher :
Kideal <- nb.familles * faitVecProb(θ.chapeau) InfFisher <- faitInfObsF(k1=Kideal[1],k2=Kideal[2],k3=Kideal[3])
Je construis l'histogramme et je superpose la densité asymptotique comme explicité dans le code ci-dessous qui donne la figure \ref{fig:Stat2013reponse9}.
par(cex=2) hist(θ.chapeau.sim, breaks=100, prob=TRUE, xlab=expression(hat(theta)), ylab="Densité estimée", main="") tt <- seq(min(θ.chapeau.sim), max(θ.chapeau.sim), len=501) lines(tt,dnorm(tt,θ.chapeau,1/sqrt(InfFisher(θ.chapeau))), col="red",lwd=2)
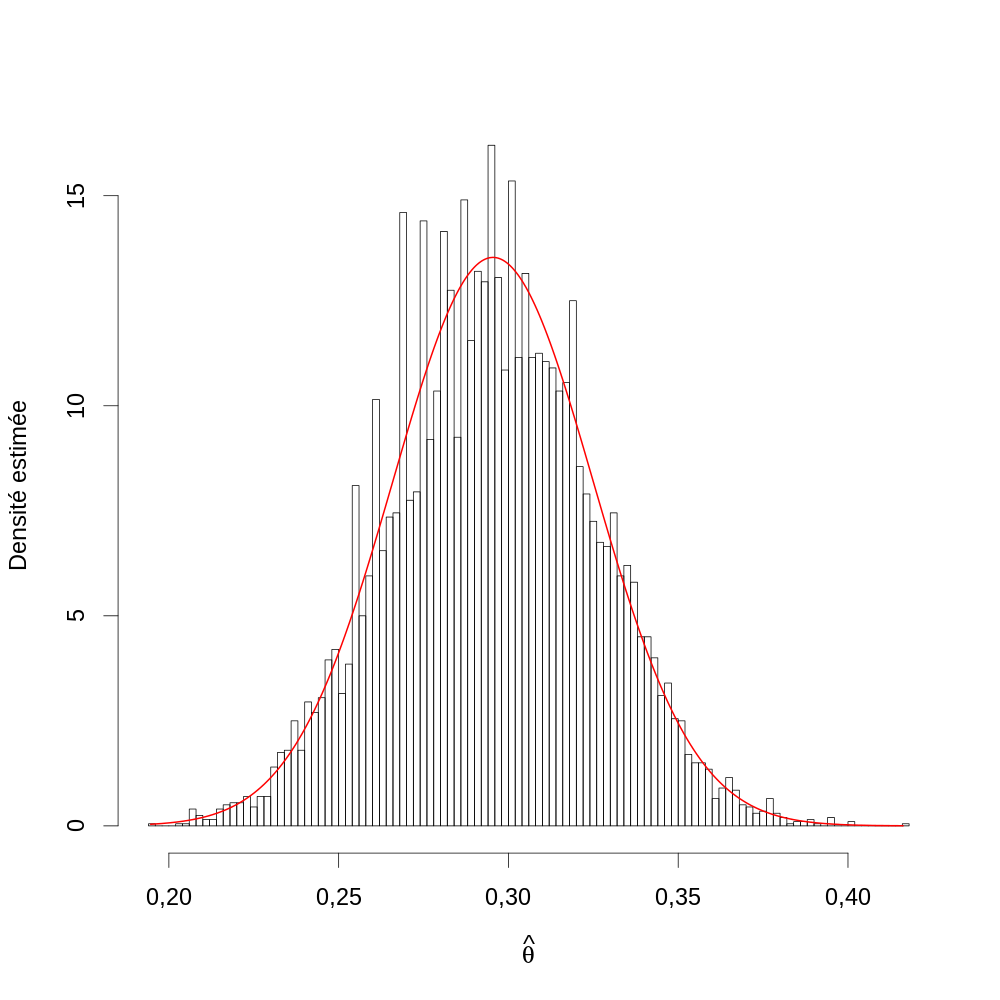
Figure 19 : Histogramme des \(\hat{\theta}\) avec la loi normale asymptotique superposée (ligne rouge).
4.1.22 Question 10
Vous construirez le hanging rootogramme vous permettant de comparer votre histogramme avec la densité théorique normale.
4.1.23 Réponse 10
On adapte les exemples du cours comme ci-dessous pour obtenir la figure \ref{fig:reponse10}.
mon.histo <- hist(θ.chapeau.sim,breaks=100,plot=FALSE) ideal <- diff(pnorm(mon.histo$breaks, θ.chapeau, 1/sqrt(InfFisher(θ.chapeau))))*n.rep par(cex=2) plot(mon.histo$mids, sqrt(mon.histo$counts) - sqrt(ideal), type="l",lwd=2, xlab=expression(hat(theta)), ylab="",main="") abline(h=c(-1,1),col=2,lty=2) abline(h=0,col="grey80")
Figure 20 : Hanging Rootogram de la densité empirique de \(\hat{\theta}\) comparée à sa densité asymptotique (une loi normale). Les lignes horizontales pointillées (rouges) correspondent à \(\pm\) 2 fois σ.
On constate que trop de points (de l'ordre de 20) sont en dehors de la bande centrale (entre les lignes pointillées rouges) qui devrait contenir en moyenne 95% des points – le rootogramme étant construit avec 100 bins. La converge de la loi de \(\hat{\theta}\) vers la loi normale n'est donc pas encore parfaite.
4.1.24 Question 11
Pour chaque expérience simulée, vous construirez un intervalle de confiance à 95% avec la méthode de Wald et vous obtiendrez la probabilité de recouvrement empirique de vos intervalles (c.-à-d. que vous obtiendrez la fraction de vos intervalles qui contiennent la vraie valeur). Commentez (c.-à-d. la méthode de Wald vous fournit-elle des intervalles de confiance à 95% fiables dans ce cas).
4.1.25 Réponse 11
dansIC95.Wald <- sapply(1:n.rep, function(i) { K <- sim.exp[,i] θ <- θ.chapeau.sim[i] JF <- faitInfObsF(k1=K[1], k2=K[2], k3=K[3]) J <- JF(θ) σ <- sqrt(1/J) IC <- θ + c(-1,1)*qnorm(0.975)*σ IC[1] <= θ.chapeau && θ.chapeau <= IC[2] }) sum(dansIC95.Wald)/length(dansIC95.Wald)
[1] 0,9484
On constate que même si le test du « rootogramme » n'était pas excellent, la probabilité de recouvrement empirique de nos intervalles de confiance à 95% obtenus avec la méthode de Wald est bonne.
4.2 Un compteur de photons à temps mort
Vous utilisez un compteur numérique de photons (à haute énergie). Votre compteur écrit les données qu'il collecte sur le disque de votre ordinateur. Les données sont les temps écoulés entre les arrivées successives de deux photons lorsque ceux-ci sont supérieurs à un « temps mort » \(\delta\). Si deux photons ou plus arrivent dans un intervalle de durée inférieure à \(\delta\), alors rien n'est enregistré. Vous êtes donc dans un contexte de données seuillées. Vous supposerez que la vraie distribution des intervalles entre temps d'arrivées est exponentielle, c'est-à-dire que la densité de probabilité pour que l'intervalle soit de durée \(t\) est : \[ p(t) = \nu \exp ( - t \nu)\; . \] Les données sont :
set.seed(123456) nu.vrai <- 7/6 delta <- 0.19 n.intervalles <- 20 itv <- qexp(runif(n.intervalles,pexp(delta,nu.vrai),1),nu.vrai) intervalles <- round(itv,digits=3) intervalles
[1] 1,560 1,391 0,615 0,548 0,574 0,379 0,846 0,277 3,970 0,347 1,561 0,962 [13] 2,210 2,013 4,552 2,130 1,998 0,379 0,540 1,477
Les données ont été arrondies à la milliseconde la plus proche, mais vous ferez comme si elles avaient été enregistrées avec une précision arbitraire. La durée du temps mort \(\delta\) est de 0,19 s.
- Question 1 : Vous obtiendrez l'expression analytique de l'estimateur du maximum de vraisemblance \(\hat{\nu}\) de \(\nu\) ainsi que sa valeur numérique basée sur l'échantillon ci-dessus.
- Question 2 : Vous obtiendrez l'erreur type \(\sigma_{\hat{\nu}}\) sur \(\hat{\nu}\). Vous en déduirez un intervalle de confiance à 95% sur \(\nu\) basé sur l'échantillon ci-dessus (comme pour la question 1, vous utiliserez la distribution asymptotique de l'EMV et la méthode de Wald).
- Question 3 : Vous tracerez le graphe du logarithme de votre fonction de vraisemblance, \(l(\nu)\), pour \(\nu \in [-3*\sigma_{\hat{\nu}} + \hat{\nu},-3*\sigma_{\hat{\nu}} + \hat{\nu}]\). Vous rajouterez à ce graphe, celui de l'approximation quadratique que vous venez de faire pour obtenir votre intervalle de confiance : \(y = l(\hat{\nu}) - (\nu - \hat{\nu})^2/(2\, \sigma^2_{\hat{\nu}})\). Commentez.
- Question 4 : Vous obtiendrez un intervalle de confiance à 95% avec un bootstrap paramétrique, c'est-à-dire que vous générerez entre 1000 et 5000 échantillons de bootstrap à partir desquels vous calculerez \(\hat{\nu}^{(B)}\). Vous utiliserez l'écart entre les quantiles correspondant à 2,5% et 97,5% de la fonction de répartition empirique de vos \(\hat{\nu}^{(B)}\), comme intervalle à 95%.
- Question 5 : Vous comparerez la moyenne de vos \(\hat{\nu}^{(B)}\) avec \(\hat{\nu}\). Que pouvez-vous dire ? Si vous avez le temps, vous pourrez refaire un bootstrap paramétrique en simulant des échantillons 100 ou 1000 fois plus grands que l'échantillon réel avant de comparer à nouveau \(\hat{\nu}^{(B)}\) avec \(\hat{\nu}\).
4.2.1 Réponse 1
La densité exponentielle « complète » est \(p(t) = \nu \exp ( - t \nu)\), la fonction de répartition est donc \[ P(t) = 1 - \exp ( - t \nu) \] et \[ \textrm{Pr}\{T > \delta\} = \exp ( - \delta \nu) \; . \] La densité de probabilité supposée pour le problème est donc : \[ p(t \mid t \ge \delta) = \nu \exp \left( - (t-\delta) \nu\right)\; . \] La log vraisemblance du problème est ainsi : \[ l(\nu) = N \, \log \nu - \nu \sum_i (t_i-\delta) \; , \] où \(N=20\) et \(i=1,\ldots,20\). La fonction score (dérivée première) est : \[ l'(\nu) = N/\nu - \sum_i (t_i - \delta) \] et la dérivée seconde est \[ l''(\nu) = -N/\nu^2\; . \] Cette dernière est toujours négative (tant que \(N>0\), ce qui est le cas ici) et \(l'\) est donc concave et admet un maximum unique donné par : \[ \hat{\nu} = N / \sum_i (t_i - \delta) \; . \] Numériquement il vient :
nu.chapeau <- 1/(mean(intervalles)-delta)
0.815361408944515
4.2.2 Réponse 2
D'après le développement de la réponse 1 on a : \[ \hat{\sigma}_{\hat{\nu}} = \hat{\nu} / \sqrt{N} \; , \] soit :
se.nu.chapeau <- nu.chapeau/sqrt(n.intervalles)
0.182320353662994
D'où l'intervalle à 95 % demandé :
round(nu.chapeau+1.96*c(-1,1)*se.nu.chapeau,digits=2)
| 0.46 |
| 1.17 |
4.2.3 Réponse 3
compte.ll <- function(nu) n.intervalles*((delta-mean(intervalles))*nu+log(nu)) nn <- seq(-3,3,len=101) * se.nu.chapeau + nu.chapeau par(cex=2) plot(nn,compte.ll(nn),type="l",lwd=2, xlab=expression(nu), ylab="log vraisemblance") lines(nn,compte.ll(nu.chapeau)-(nn-nu.chapeau)^2/2/se.nu.chapeau^2,col=2) abline(v=-1.96*se.nu.chapeau + nu.chapeau,lty=2) abline(v=1.96*se.nu.chapeau + nu.chapeau,lty=2)
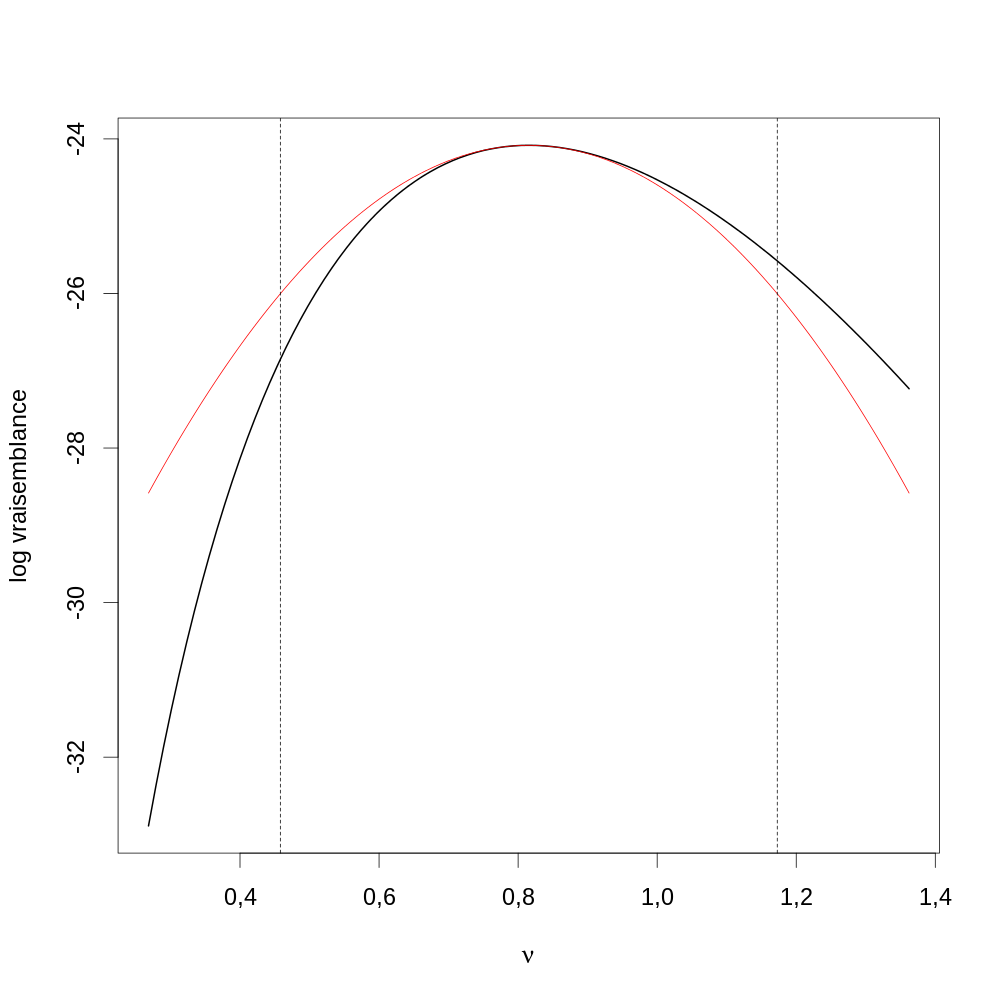
Figure 21 : Logarithme de la fonction de vraisemblance au voisinage de son maximum. En rouge, l'approximation quadratique sur laquelle le calcul des intervalles de confiance est basé. En pointillés, les limites de l'intervalle de confiance à 95 %.
On voit que l'approximation quadratique commence à être « assez loin » de la fonction approximée. Cela suggère que l'intervalle de confiance que nous venons d'obtenir n'est pas très fiable.
4.2.4 Réponse 4
set.seed(225246) nu.chapeau.boot.echantillon <- sapply(1:5000, function(i) 1/(mean(qexp(runif(n.intervalles, pexp(delta,nu.chapeau),1), nu.chapeau) )-delta ) ) round(quantile(nu.chapeau.boot.echantillon,probs=c(0.025,0.975)),digits=2)
| 0.55 |
| 1.33 |
On voit que l'intervalle de bootstrap est « décalé » vers la droite par-rapport à l'intervalle obtenu avec l'approximation normale. Ceci est cohérent avec la différence entre l'approximation quadratique et la fonction de log vraisemblance.
4.2.5 Réponse 5
La moyenne de l'estimateur de bootstrap est :
mean(nu.chapeau.boot.echantillon)
0.860996385694117
Cet estimateur est :
nu.chapeau.boot.moy <- mean(nu.chapeau.boot.echantillon) nu.chapeau.boot.se <- sd(nu.chapeau.boot.echantillon)/sqrt(length(nu.chapeau.boot.echantillon)) pnorm((nu.chapeau-nu.chapeau.boot.moy)/nu.chapeau.boot.se)
1.1862179628973e-56
significativement différent de \(\hat{\nu}\). Cela signifie que l'estimateur du maximum de vraisemblance est biaisé pour une taille d'échantillon aussi petite. Avec un échantillon de taille 100 fois plus grance nous aurions :
set.seed(231815) nu.chapeau.boot.echantillon2 <- sapply(1:1000, function(i) 1/(mean(round(qexp(runif(n.intervalles*100, pexp(delta,nu.chapeau), 1), nu.chapeau ), digits=3) )-delta ) ) nu.chapeau.boot.moy2 <- mean(nu.chapeau.boot.echantillon2) nu.chapeau.boot.se2 <- sd(nu.chapeau.boot.echantillon2)/sqrt(length(nu.chapeau.boot.echantillon2)) pnorm((nu.chapeau-nu.chapeau.boot.moy2)/nu.chapeau.boot.se2)
0.183803649654853
Le biais disparaît.
4.3 Données censurées ou tronquées
Une entreprise développe un composant (par exemple un nouveau type de disque dur) et cherche à quantifier la fiabilité de celui-ci. Des tests sont conçus à cette fin et consistent à choisir au hasard 10 des composants à la sortie de la chaîne de production, à les installer dans dix machines identiques puis à solliciter les composants à « plein régime » jusqu'à ce qu'ils aient une panne. D'une façon générale, les 10 composants vont subir des pannes à des temps différents et ce qui intéresse les ingénieurs est l'estimation du temps moyen jusqu'à la panne. Supposons que 3 cas de figures se présentent:
- les tests des 10 composants sont effectués simultanément et les observations sont poursuivies jusqu'à ce que chaque composant ait subi une panne.
- les tests des 10 composants sont effectués simultanément et les observations sont poursuivies jusqu'à ce que chaque composant ait subi une panne ou que 50 jours se soient écoulés. La « durée de vie » des composants n'ayant pas subi de pannes après 50 jours est dîtes censurée et est alors notée
50+(le+signalant la censure). - les tests des 10 composants sont effectués simultanément et les observations sont poursuivies jusqu'à ce que chaque composant ait subi une panne ou que 25 jours se soient écoulés. La durée de vie des composant encore actif à la fin des observations est notée de façon similaire
25+.
On pourrait ainsi avoir les données suivantes correspondants au trois cas de figure:
| id. du composant | durée de vie – Cas 1 | durée de vie – Cas 2 | durée de vie – Cas 3 |
|---|---|---|---|
| 1 | 70 | 50+ | 25+ |
| 2 | 11 | 11 | 11 |
| 3 | 66 | 50+ | 25+ |
| 4 | 5 | 5 | 5 |
| 5 | 20 | 20 | 20 |
| 6 | 4 | 4 | 4 |
| 7 | 35 | 35 | 25+ |
| 8 | 40 | 40 | 25+ |
| 9 | 29 | 29 | 25+ |
| 10 | 8 | 8 | 8 |
Vous supposerez que les durées de vie des composants suivent une loi exponentielle et vous écrirez la vraisemblance : \[ \mathcal{L}(\nu) = \prod_{i=1}^{10} \left(\nu \, \exp( -\nu t_i)\right)^{1-I_C(t_i)} \, \left(\exp(-\nu T)\right)^{I_C(t_i)} \; , \] où \(T\) est la durée maximale d'observation (\(+ \infty\) dans le cas 1, 50 dans le cas 2 et 25 dans le cas 3), \(I_C\) est la fonction indicatrice de l'ensemble \(C = \{t \in \mathbb{R}^+ \, | \, t > T\}\) :
\[ I_{C}(t) = \begin{cases} 1 & \textrm{si} \; t \in C \\ 0 & \textrm{sinon} \end{cases} \]
- Question 1 : vous trouverez l'expression analytique de l'estimateur du maximum de vraisemblance dans les 3 cas ainsi que les valeurs numériques correspondantes.
- Question 2 : vous obtiendrez des intervalles de confiances à 95% dans les trois cas en utilisant la distribution asymptotique de l'EMV comme dans les questions précédentes (sur le détecteur à temps mort).
- Question 3 : vous tracerez sur une seule figure les graphes des logarithmes des fonctions de vraisemblance et de leurs approximations quadratiques (comme dans la question 3 sur le détecteur à temps mort). Commentez.
- Question 4 : vous obtiendrez des intervalles de confiance à 95 % avec un bootstrap paramétrique comme pour le détecteur à temps mort pour chacun des trois cas.
4.3.1 Réponse 1
Notons \(N_T=10\) la taille de l'échantillon et \(0 \le m \le N_T\) le nombre d'observations censurées, c.-à-d. le cardinal de l'ensemble \(C\) de l'équation (dans le premier cas, \(m=0\)). Comme les observations sont (supposées) IID nous pouvons réarranger les indices sans perte de généralité, de sorte que les \(N_T-m\) premiers indices correspondent aux observations non censurées. La log vraisemblance peut alors s'écrire : \[ l(\nu) = (N_T-m) \, \log \nu - \nu \, \sum_{i=1}^{N_T-m} t_i - \nu \, m \, T \; . \] La fonction score est donc : \[ l'(\nu) = \frac{N_T-m}{\nu} - \left( \sum_{i=1}^{N_T-m} t_i + m \, T\right) \] et la dérivée seconde est : \[ l''(\nu) = - \frac{N_T-m}{\nu^2} \; . \] Tant que toutes les observations ne sont pas censurées \(l'\) est donc concave et admet un unique maximum. Dans le cas contraire la vraisemblance est maximale en \(\nu = 0\). Comme dans chacun de nos trois cas, l'échantillon contient des éléments non censurés, nous avons : \[ \hat{\nu} = \frac{N_T-m}{N_T \, \bar{t}} \; , \] où \[ \bar{t} = \frac{1}{N_T} \left( \sum_{i=1}^{N_T-m} t_i + m \, T\right) \; . \]
Pour chacun des trois cas nous avons donc :
durées1 <- c(70,11,66,5,20,4,35,40,29,8) m.cas.1 <- 0 t.bar.cas.1 <- mean(durées1) durées2 <- c(50,11,50,5,20,4,35,40,29,8) m.cas.2 <- sum(durées2 == 50) t.bar.cas.2 <- mean(durées2) durées3 <- c(25,11,25,5,20,4,25,25,25,8) m.cas.3 <- sum(durées3 == 25) t.bar.cas.3 <- mean(durées3) N.T <- length(durées1) ν.cas.1 <- (N.T-m.cas.1)/N.T/t.bar.cas.1 ν.cas.2 <- (N.T-m.cas.2)/N.T/t.bar.cas.2 ν.cas.3 <- (N.T-m.cas.3)/N.T/t.bar.cas.3 ν <- c(ν.cas.1,ν.cas.2,ν.cas.3) data.frame(cas=paste("cas",1:3), ν=round(ν,digits=4) )
| cas 1 | 0.0347 |
| cas 2 | 0.0317 |
| cas 3 | 0.0289 |
4.3.2 Réponse 2
Le développement précédent nous donne : \[ \hat{\sigma}_{\hat{\nu}} = \frac{\nu}{\sqrt{N_T-m}} \; , \] d'où :
σ <- ν / sqrt(N.T-c(m.cas.1,m.cas.2,m.cas.3)) ic.ν <- cbind(-1.96 * σ,+1.96 * σ) + ν round(ic.ν,digits=4)
| 0.0132 | 0.0562 |
| 0.0097 | 0.0537 |
| 0.0036 | 0.0542 |
4.3.3 Réponse 3
mkLLFct <- function(durées, m ) { t.bar <- mean(durées) N.T <- length(durées) facteur <- N.T-m function(ν) facteur * log(ν) - ν*N.T*t.bar } llFct.cas1 <- mkLLFct(durées1,m.cas.1) llFct.cas2 <- mkLLFct(durées2,m.cas.2) llFct.cas3 <- mkLLFct(durées3,m.cas.3) ν.lim <- c(min(ic.ν[,1]),max(ic.ν[,2])) νν <- seq(ν.lim[1],ν.lim[2],len=101) par(cex=2) plot(νν, llFct.cas1(νν)-llFct.cas1(ν[1]), type="l", xlab="ν", ylab="log vraisemblance - log vraisemblance maximale", lwd=2, col=1, ylim=c(-6,0)) lines(νν, - (νν-ν[1])^2/2/σ[1]^2, lwd=2,lty=2,col=1) lines(νν, llFct.cas2(νν)-llFct.cas2(ν[2]), lwd=2,lty=1,col=2) lines(νν, - (νν-ν[2])^2/2/σ[2]^2, lwd=2,lty=2,col=2) lines(νν, llFct.cas3(νν) - llFct.cas3(ν[3]), lwd=2,lty=1,col=4) lines(νν, - (νν-ν[3])^2/2/σ[3]^2, lwd=2,lty=2,col=4)
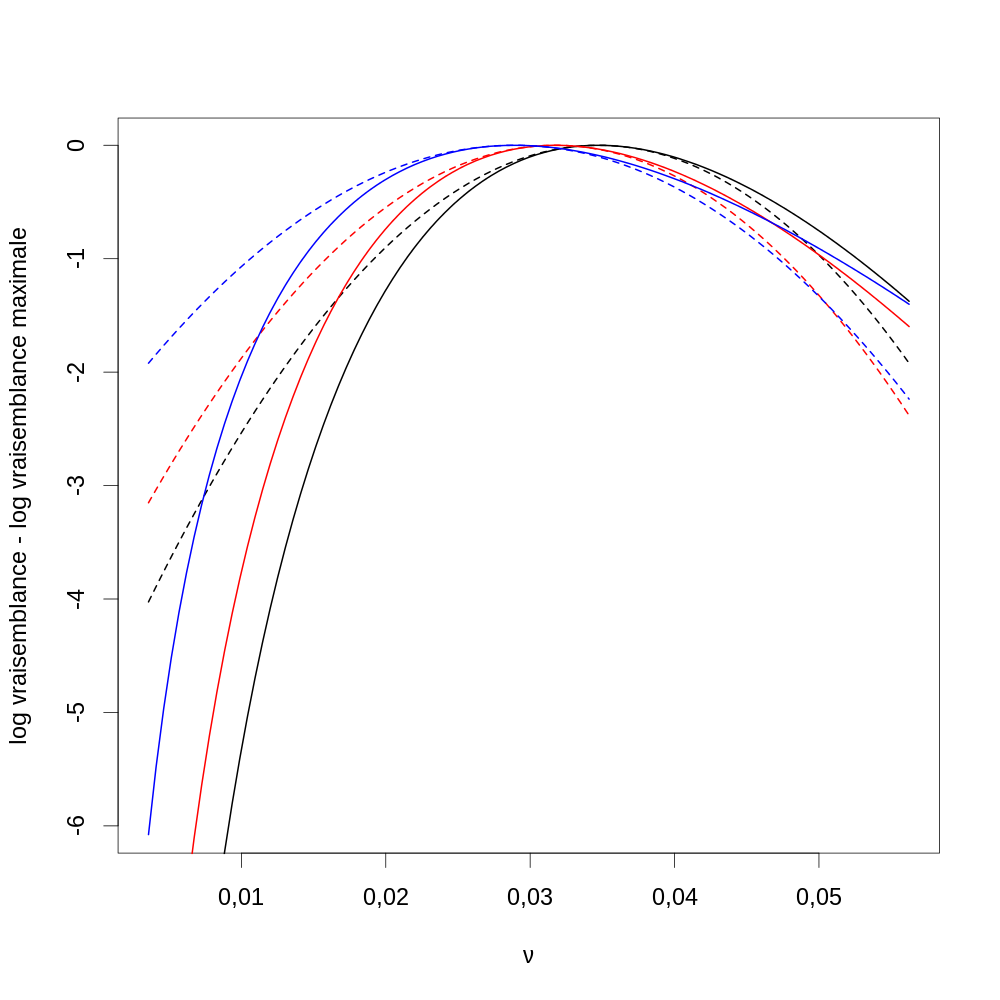
Figure 22 : Pour plus de clarté on a tracé la log vraisemblance « relative au maximum» (\(l(\nu) - l(\hat{\nu})\)). En noir, le cas 1; en rouge, le cas 2; en bleu, le cas 3.
On constate que l'approximation quadratique n'est jamais bonne. De plus les 3 courbes diffèrent le plus pour les petites valeurs de ν, ce qui est normal car ce sont les grandes valeurs de temps de pannes qui donnent de l'information « de ce coté là » et ce sont les valeurs censurées dans les cas 2 et 3.
4.3.4 Réponse 4
On procède comme suit :
set.seed(141718) n.boot <- 1000 ν.boot.cas.1 <- sapply(1:n.boot, function(i) { durées <- rexp(N.T,ν[1]) 1/mean(durées) } ) μ.ν.boot.cas.1 <- mean(ν.boot.cas.1) σ.ν.boot.cas.1 <- sd(ν.boot.cas.1)/sqrt(n.boot) pnorm((ν[1]-μ.ν.boot.cas.1)/σ.ν.boot.cas.1) ν.boot.cas.2 <- sapply(1:n.boot, function(i) { durées <- rexp(N.T,ν[2]) durées[durées>=50] <- 50 m <- sum(durées==50) (N.T-m)/N.T/mean(durées) } ) μ.ν.boot.cas.2 <- mean(ν.boot.cas.2) σ.ν.boot.cas.2 <- sd(ν.boot.cas.2)/sqrt(n.boot) pnorm((ν[2]-μ.ν.boot.cas.2)/σ.ν.boot.cas.2) ν.boot.cas.3 <- sapply(1:n.boot, function(i) { durées <- rexp(N.T,ν[3]) durées[durées>=25] <- 25 m <- sum(durées==25) (N.T-m)/N.T/mean(durées) } ) μ.ν.boot.cas.3 <- mean(ν.boot.cas.3) σ.ν.boot.cas.3 <- sd(ν.boot.cas.3)/sqrt(n.boot) pnorm((ν[3]-μ.ν.boot.cas.3)/σ.ν.boot.cas.3) ic.ν.boot <- rbind(quantile(ν.boot.cas.1,probs=c(0.025,0.975)), quantile(ν.boot.cas.2,probs=c(0.025,0.975)), quantile(ν.boot.cas.3,probs=c(0.025,0.975)) ) round(ic.ν.boot,digits=4)
| 0.0197 | 0.072 |
| 0.0127 | 0.0645 |
| 0.0088 | 0.0636 |
5 Examen du 6 juin 2013
Les deux problèmes ci-dessous sont tirés du livre de John Rice cité au début de ce document :
- le premier problème est tiré de l'exemple 14.2.4 ;
- le second problème est tiré de l'exercice 8.45.
5.1 Régression linéaire : cancer du sein
Le fichier http://xtof.disque.math.cnrs.fr/data/CoursStat2013cancer.txt contient le nombre de décès dus à un cancer du sein entre 1950 et 1960 (première colonne) ainsi que la population féminine adulte en 1960 (seconde colonne) pour 301 comtés de Caroline du Nord, Caroline du Sud et Géorgie (aux États-Unis).
Vous commencerez par charger ces données dans votre espace de travail avec, par exemple :
cancer <- read.csv("http://xtof.disque.math.cnrs.fr/data/CoursStat2013cancer.txt", header=FALSE)
| 1 | 445 |
| 0 | 559 |
| 3 | 677 |
| 4 | 681 |
| 3 | 746 |
| 4 | 869 |
| 1 | 950 |
| 5 | 976 |
| 5 | 1096 |
| 5 | 1098 |
| 5 | 1114 |
| 7 | 1125 |
| 5 | 1236 |
| 6 | 1285 |
| 3 | 1291 |
| 3 | 1318 |
| 2 | 1323 |
| 8 | 1327 |
| 9 | 1438 |
| 7 | 1479 |
| 4 | 1536 |
| 6 | 1598 |
| 6 | 1635 |
| 11 | 1667 |
| 4 | 1696 |
| 7 | 1792 |
| 7 | 1795 |
| 4 | 1808 |
| 6 | 1838 |
| 16 | 1838 |
| 3 | 1847 |
| 8 | 1933 |
| 8 | 1959 |
| 4 | 1990 |
| 9 | 2003 |
| 10 | 2070 |
| 7 | 2091 |
| 8 | 2099 |
| 5 | 2104 |
| 11 | 2147 |
| 4 | 2154 |
| 12 | 2163 |
| 11 | 2172 |
| 9 | 2174 |
| 13 | 2183 |
| 17 | 2193 |
| 11 | 2210 |
| 10 | 2212 |
| 4 | 2236 |
| 4 | 2245 |
| 8 | 2261 |
| 6 | 2317 |
| 8 | 2333 |
| 16 | 2393 |
| 10 | 2404 |
| 4 | 2419 |
| 11 | 2462 |
| 10 | 2476 |
| 11 | 2477 |
| 9 | 2483 |
| 11 | 2511 |
| 14 | 2591 |
| 6 | 2624 |
| 8 | 2690 |
| 12 | 2731 |
| 15 | 2735 |
| 9 | 2736 |
| 13 | 2747 |
| 18 | 2782 |
| 15 | 2783 |
| 12 | 2793 |
| 11 | 2891 |
| 12 | 2894 |
| 12 | 2906 |
| 14 | 2929 |
| 12 | 2935 |
| 3 | 2962 |
| 5 | 3054 |
| 7 | 3112 |
| 9 | 3118 |
| 11 | 3185 |
| 14 | 3217 |
| 18 | 3236 |
| 11 | 3290 |
| 11 | 3314 |
| 4 | 3316 |
| 13 | 3401 |
| 10 | 3409 |
| 10 | 3426 |
| 9 | 3470 |
| 11 | 3488 |
| 12 | 3511 |
| 4 | 3549 |
| 16 | 3571 |
| 20 | 3578 |
| 5 | 3620 |
| 15 | 3654 |
| 15 | 3680 |
| 12 | 3683 |
| 7 | 3688 |
| 7 | 3706 |
| 12 | 3733 |
| 21 | 3800 |
| 16 | 3802 |
| 13 | 3832 |
| 16 | 3863 |
| 8 | 3891 |
| 12 | 4008 |
| 20 | 4093 |
| 21 | 4149 |
| 15 | 4162 |
| 13 | 4223 |
| 13 | 4232 |
| 10 | 4312 |
| 22 | 4329 |
| 14 | 4331 |
| 16 | 4399 |
| 13 | 4470 |
| 24 | 4618 |
| 27 | 4669 |
| 16 | 4681 |
| 28 | 4737 |
| 11 | 4784 |
| 12 | 4829 |
| 14 | 4857 |
| 26 | 4918 |
| 27 | 4967 |
| 17 | 5041 |
| 20 | 5051 |
| 12 | 5077 |
| 20 | 5107 |
| 12 | 5108 |
| 24 | 5124 |
| 27 | 5156 |
| 25 | 5167 |
| 19 | 5211 |
| 21 | 5246 |
| 8 | 5743 |
| 15 | 5773 |
| 22 | 5932 |
| 21 | 5983 |
| 37 | 5989 |
| 23 | 5998 |
| 18 | 6021 |
| 25 | 6035 |
| 26 | 6074 |
| 17 | 6134 |
| 27 | 6175 |
| 13 | 6220 |
| 13 | 6296 |
| 15 | 6445 |
| 33 | 6624 |
| 24 | 6841 |
| 23 | 6868 |
| 18 | 6903 |
| 24 | 6904 |
| 21 | 6916 |
| 32 | 6934 |
| 23 | 6978 |
| 32 | 7014 |
| 16 | 7025 |
| 29 | 7031 |
| 33 | 7115 |
| 20 | 7256 |
| 19 | 7288 |
| 27 | 7304 |
| 10 | 7367 |
| 34 | 7376 |
| 36 | 7407 |
| 26 | 7408 |
| 33 | 7503 |
| 24 | 7599 |
| 37 | 7743 |
| 34 | 7760 |
| 37 | 7910 |
| 20 | 7917 |
| 28 | 7957 |
| 30 | 7984 |
| 27 | 8004 |
| 45 | 8208 |
| 39 | 8249 |
| 29 | 8289 |
| 22 | 8313 |
| 27 | 8377 |
| 19 | 8396 |
| 30 | 8468 |
| 34 | 8493 |
| 35 | 8531 |
| 21 | 8773 |
| 18 | 8866 |
| 41 | 9091 |
| 34 | 9215 |
| 51 | 9225 |
| 30 | 9243 |
| 32 | 9435 |
| 38 | 9445 |
| 18 | 9468 |
| 42 | 9563 |
| 60 | 9605 |
| 19 | 9841 |
| 29 | 9994 |
| 17 | 10033 |
| 29 | 10049 |
| 41 | 10144 |
| 31 | 10303 |
| 35 | 10416 |
| 27 | 10461 |
| 37 | 10670 |
| 18 | 10844 |
| 41 | 10875 |
| 39 | 10890 |
| 41 | 11105 |
| 61 | 11622 |
| 46 | 12038 |
| 47 | 12173 |
| 36 | 12181 |
| 43 | 12608 |
| 45 | 12775 |
| 46 | 12915 |
| 45 | 13021 |
| 49 | 13142 |
| 55 | 13206 |
| 64 | 13407 |
| 64 | 13647 |
| 66 | 13870 |
| 57 | 13989 |
| 53 | 14089 |
| 51 | 14197 |
| 36 | 14620 |
| 28 | 14816 |
| 59 | 14952 |
| 39 | 15039 |
| 73 | 15049 |
| 41 | 15179 |
| 48 | 15204 |
| 37 | 16161 |
| 72 | 16239 |
| 72 | 16427 |
| 48 | 16462 |
| 62 | 16793 |
| 51 | 16925 |
| 71 | 17027 |
| 60 | 17201 |
| 70 | 17526 |
| 59 | 17666 |
| 91 | 17692 |
| 52 | 17742 |
| 65 | 18482 |
| 77 | 18731 |
| 84 | 18835 |
| 51 | 19274 |
| 66 | 19818 |
| 53 | 19906 |
| 58 | 20065 |
| 75 | 20140 |
| 88 | 20268 |
| 83 | 20539 |
| 48 | 20639 |
| 69 | 20969 |
| 41 | 21353 |
| 73 | 21757 |
| 79 | 22811 |
| 63 | 23245 |
| 90 | 23258 |
| 92 | 24296 |
| 60 | 24351 |
| 63 | 24692 |
| 63 | 24896 |
| 75 | 25275 |
| 70 | 25405 |
| 90 | 25715 |
| 111 | 26245 |
| 103 | 26408 |
| 117 | 26691 |
| 118 | 28024 |
| 40 | 28270 |
| 83 | 28477 |
| 90 | 29254 |
| 97 | 29422 |
| 92 | 30125 |
| 104 | 30538 |
| 96 | 34109 |
| 142 | 35112 |
| 105 | 35876 |
| 145 | 36307 |
| 160 | 39023 |
| 127 | 40756 |
| 169 | 42997 |
| 104 | 47672 |
| 179 | 49126 |
| 152 | 53464 |
| 163 | 56529 |
| 167 | 59634 |
| 302 | 60161 |
| 246 | 62398 |
| 236 | 62652 |
| 250 | 62931 |
| 267 | 63476 |
| 244 | 66676 |
| 248 | 74005 |
| 360 | 88456 |
- Question 1.1 : vous construirez un graphe en nuage de points, avec des labels adaptés, du nombre de décès par cancer en fonction de la population féminine adulte.
- Question 1.2 : vous estimerez le paramètre β du modèle linéaire sans ordonnée à l'origine : \[\textrm{nombre de décès} = β \times \textrm{population} \, ,\] (soit en passant vous-même par la décomposition QR, soit en utilisant la fonction
lm). - Question 1.3 : vous effectuerez les tests d'adéquation graphiques et vous commenterez.
- Question 1.4 : les données étant des comptes (les valeurs sont forcément des entiers positifs ou nuls), vous penserez, en bons statisticiens, à une loi de Poisson et, en vous inspirant du développement qui nous a amené au hanging rootogram (section 3.6.1 du cours), vous ajusterez le modèle : \[\textrm{f(nombre de décès)} = γ \times \textrm{f(population)} \, , \] (dans les deux membres, c'est la même fonction
f, que vous trouverez). Vous estimerez γ et vous construirez vos graphes de diagnostique. - Question 1.5 : vous obtiendrez un intervalle de confiance à 95% pour γ (comme dans la section 2.2.2.6 du cours).
5.2 Réponses
5.2.1 Question 1.1
Une fois les données chargées dans l'espace de travail, il suffit de faire :
par(cex=2) with(cancer,plot(V2,V1, xlab="Population féminine adulte (1960)", ylab="Nombre de décès par cancer du sein (1950-1960)"))
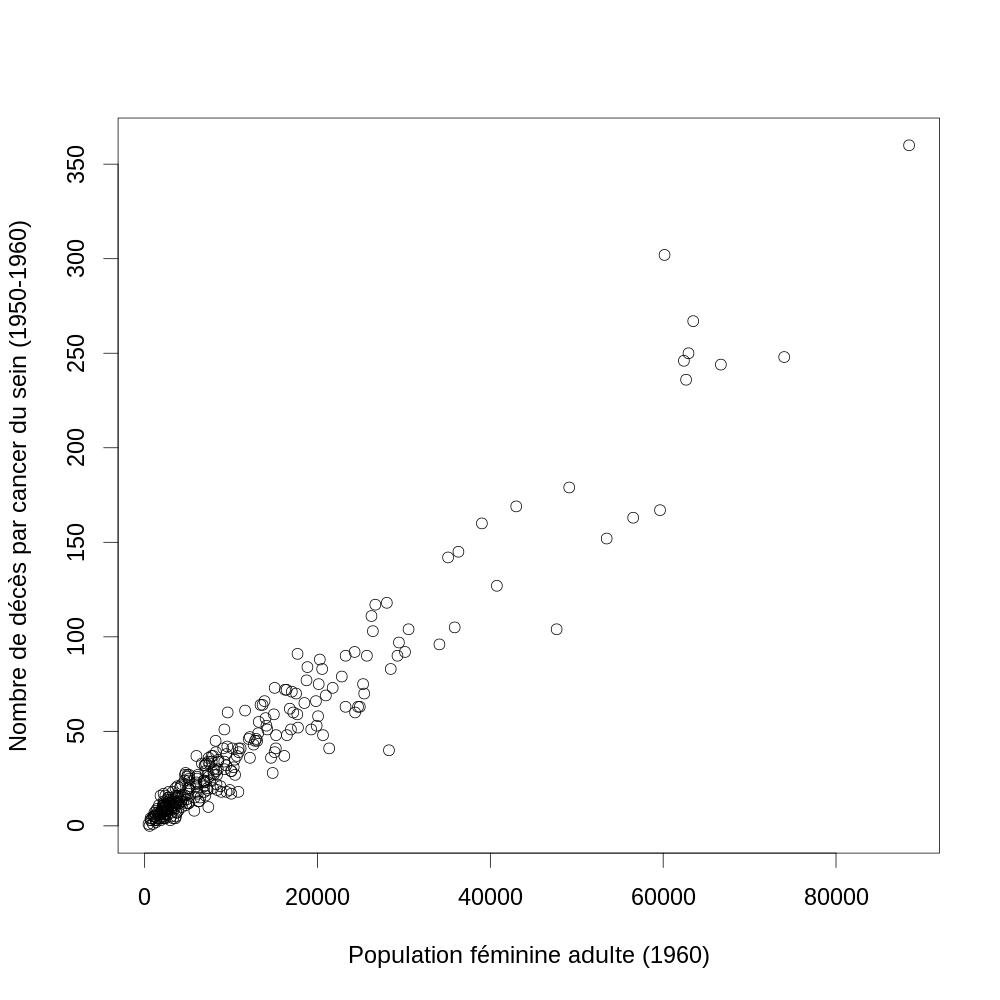
Figure 23 : Le nombre de décès par cancer du sein (entre 1950 et 1960) en fonction de la population féminine adulte (en 1960) pour les comtés de trois états des États-Unis (Caroline du Nord, Caroline du Sud et Géorgie).
5.2.2 Question 1.2
La façon la plus directe de précéder dans R est d'utiliser la fonction lm. La seule petite subtilité vient du fait qu'on ne veut pas d'ordonnée à l'origine dans le modèle, ce qui nous donne l'appel suivant :
cancer.fit <- lm(V1 ~ V2 - 1, data=cancer)
summary(cancer.fit)
Call:
lm(formula = V1 ~ V2 - 1, data = cancer)
Residuals:
Min 1Q Median 3Q Max
-65.654 -4.428 0.245 4.779 87.901
Coefficients:
Estimate Std. Error t value Pr(>|t|)
V2 3.559e-03 4.205e-05 84.62 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12.98 on 300 degrees of freedom
Multiple R-squared: 0.9598, Adjusted R-squared: 0.9597
F-statistic: 7161 on 1 and 300 DF, p-value: < 2.2e-16
Cela nous donne directement notre estimation \(\hat{β}\) de β : \(3.56 \times 10^{-3}\).
La méthode plus générale passe par la construction de la matrice du plan d'expérience :
X <- cbind(cancer$V2)
suivie par la décomposition QR et la « récupération » des matrices Q et R :
XdecompQR <- qr(X) Q <- qr.Q(XdecompQR) R <- qr.R(XdecompQR)
et l'estimateur est obtenu par :
(beta.chapeau <- backsolve(R, t(Q) %*% cancer$V1))
0.00355876748882502
5.2.3 Question 1.3
Si la fonction lm a été utilisée, il suffit d'appeler la fonction plot sur l'objet cancer.fit pour générer les graphes de diagnostique :
plot(cancer.fit)
Ce sont les deux premiers graphes générés par cette commande que je vous ai dit de toujours faire.
Si la « voie QR » a été choisie il fallait faire quelque chose du type :
layout(matrix(c(1:3,3),nc=2,byrow=TRUE)) par(cex=2) with(cancer,plot(V2,V1,col="blue",xlab="Population",ylab="Décès")) domaine.pop <- range(cancer$V2) dd <- seq(domaine.pop[1],domaine.pop[2],len=501) lines(dd,dd %*% beta.chapeau,col="red",lwd=2) Y.chapeau <- X %*% beta.chapeau Z.chapeau <- cancer$V1 - Y.chapeau qqnorm(Z.chapeau, col="blue",main="", xlab="Quantiles théoriques (loi normale)",ylab="Quantiles empiriques") qqline(Z.chapeau,col="red",lwd=2) plot(Y.chapeau, Z.chapeau, col="blue",xlab="Valeurs prédites",ylab="Résidus") abline(h=0,col="red",lwd=2)
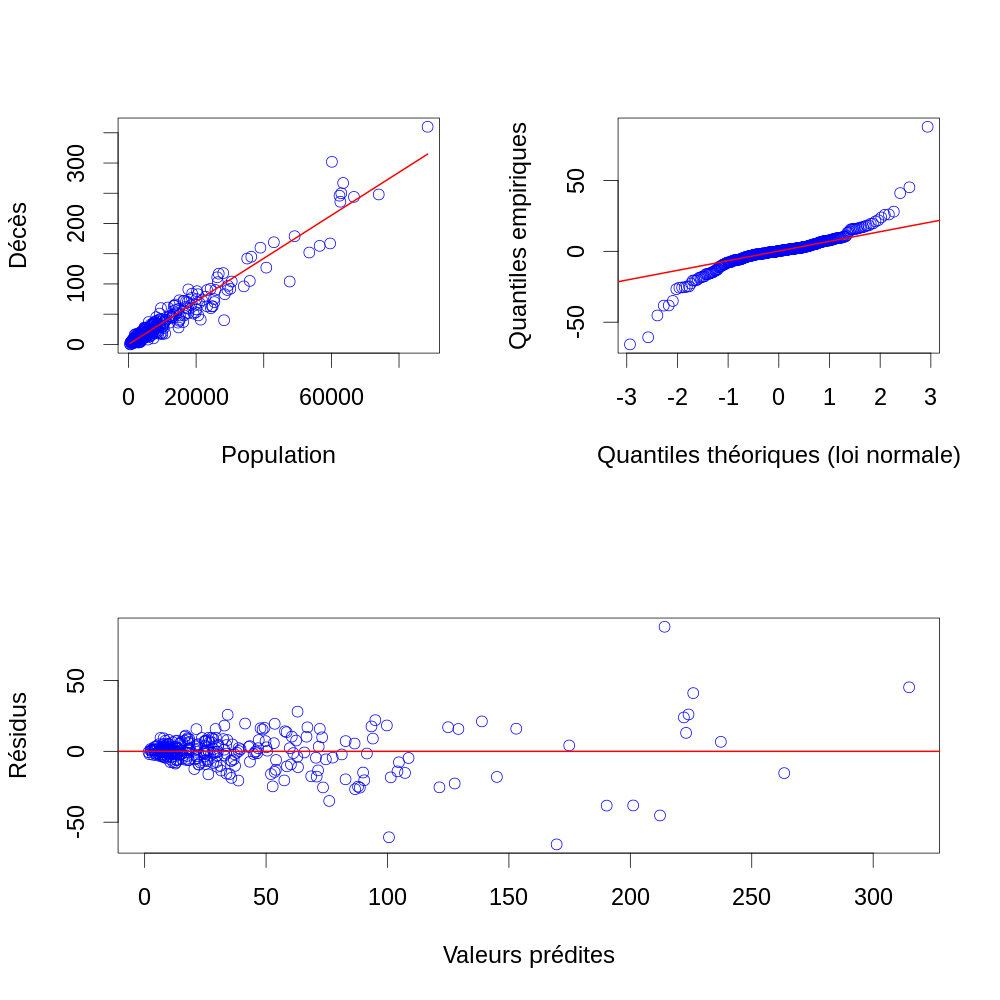
Figure 24 : Le nombre de décès par cancer du sein (entre 1950 et 1960) en fonction de la population féminine adulte (en 1960) pour les comtés de trois états des États-Unis (Caroline du Nord, Caroline du Sud et Géorgie) avec modèle ajusté (en haut à gauche). Résidus en fonction de la valeur prédite (en bas). Graphe quantile-quantile des résidus (en haut à droite).
Ici il y a une dépendance nette de la variance des résidus vis-à-vis de la valeur prédite. Les résidus ne suivent pas non plus une loi normale. Ceci signifie que les hypothèses requises pour construire un intervalle de confiance ayant un sens ne sont pas vérifiées. C'est pourquoi nous allons chercher une transformation stabilisant la variance.
5.2.4 Question 1.4
Quand les données sont susceptibles de venir d'une loi de Poisson, la transformation à essayer en priorité est la transformation racine carrée (précisément celle qui est employée dans la construction d'un hanging rootogram). Je donne maintenant la version « longue » passant par la décomposition QR :
Xs <- cbind(sqrt(cancer$V2)) XdecompQRs <- qr(Xs) Qs <- qr.Q(XdecompQRs) Rs <- qr.R(XdecompQRs) (gamma.chapeau <- backsolve(Rs, t(Qs) %*% sqrt(cancer$V1)))
0.058918594589966
Et les graphes suivent :
layout(matrix(c(1:3,3),nc=2,byrow=TRUE)) par(cex=2) with(cancer,plot(sqrt(V2),sqrt(V1),col="blue",xlab="Population^1/2",ylab="Décès^1/2")) domaine.pops <- range(sqrt(cancer$V2)) dds <- seq(domaine.pops[1],domaine.pops[2],len=501) lines(dds,dds %*% gamma.chapeau,col="red",lwd=2) Ys.chapeau <- Xs %*% gamma.chapeau Zs.chapeau <- sqrt(cancer$V1) - Ys.chapeau qqnorm(Zs.chapeau, col="blue",main="", xlab="Quantiles théoriques (loi normale)",ylab="Quantiles empiriques") qqline(Zs.chapeau,col="red",lwd=2) plot(Ys.chapeau, Zs.chapeau, col="blue",xlab="Valeurs prédites",ylab="Résidus") abline(h=0,col="red",lwd=2)
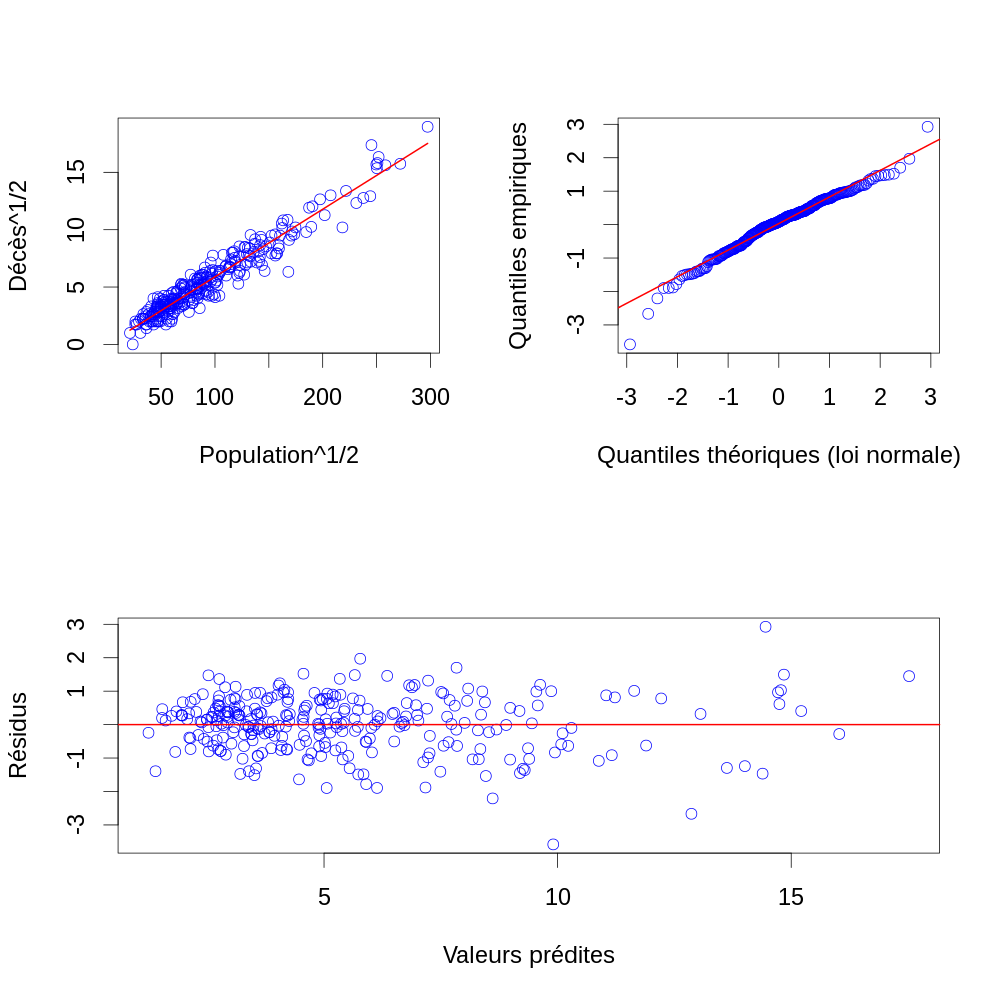
Figure 25 : La racine carrée du nombre de décès par cancer du sein (entre 1950 et 1960) en fonction de la racine carrée de la population féminine adulte (en 1960) pour les comtés de trois états des États-Unis (Caroline du Nord, Caroline du Sud et Géorgie) avec modèle ajusté (en haut à gauche). Résidus en fonction de la valeur prédite (en bas). Graphe quantile-quantile des résidus (en haut à droite).
La transformation racine carrée a nettement atténué la non homogénéité de la variance. Les résidus sont aussi nettement plus proches d'une loi normale. On peut donc calculer une erreur type reposant sur l'hypothèse d'un bruit homogène suivant une loi normale.
5.2.5 Question 1.5
On suit la section 2.2.2.6 du cours pour obtenir :
sigma2.chapeau <- sum(Zs.chapeau^2)/-diff(dim(Xs)) gamma.chapeau.se <- sqrt(sigma2.chapeau*diag(solve(t(Rs) %*% Rs))) (gamma.chapeau.ci <- qt(c(0.025,0.975),-diff(dim(Xs)))*gamma.chapeau.se+gamma.chapeau)
| 0.0580421079569477 |
| 0.0597950812229843 |
5.3 Maximum de vraisemblance : structure de l'ADN
L'ADN chez les eukaryotes, groupe d'organismes dont nous faisons parti et dont les cellules contiennent un noyau, présente des structure à de nombreuses échelles différentes comme l'illustre la figure ci-dessous3 :
Les données que vous allez analyser portent sur la structure visible sur le quatrième panneau (en partant de la gauche) formée par les brins d'ADN de 30 nm de diamètre associés aux protéines de structure (scaffold protein). Les modèles utilisés pour décrire ces structures sont en fait simples voir très simples :
- les gens considèrent les boucles individuels – formées par le brin de 30 nm de diamètre entre deux contacts avec l'élément de structure, visibles sur le troisième panneau – comme des unités « homogènes » assimilables aux monomères d'un polymère linéaire ;
- la chaîne de monomères est modélisée comme une marche aléatoire à 3D (je sais, c'est un peu grossier comme hypothèse !), c'est-à-dire qu'on suppose que l'espace euclidien à 3D est équipé d'un réseau uniforme, que les monomères peuvent occuper les noeuds de ce réseau et que la chaîne est construite en ajoutant les monomères successifs au hasard parmi les 6 noeuds plus proches voisins, même s'ils sont déjà occupés ;
- la distance euclidienne entre deux éléments de la chaîne doit alors suivre une distribution gaussienne isotrope à 3D.
Expérimentalement, les gens peuvent marquer, avec des molécules fluorescentes, des séquences spécifiques de l'ADN d'un chromosome. Il est alors possible de tester expérimentalement le modèle simple « de marche aléatoire » de la façon suivante :
- deux morceaux d'un chromosome dont la séparation « linéaire » mesurée en millions de paires de bases (Mbp) est connue sont marqués ;
- une centaine de cellules, toutes marquées de façon identique et préparées dans les mêmes conditions, sont congelées très rapidement et « fixées » chimiquement ;
- la distance euclidienne entre les deux marques est mesurée dans le plan focal d'un microscope à fluorescence ;
- la projection dans le plan d'une gaussienne à 3D étant une gaussienne à 2D, la distance entre les marques doit suivre une loi de Rayleigh4 dont la densité est : \[f(r|θ) = \frac{r}{θ^2} \exp \left(\frac{-r^2}{2θ^2}\right)\, , \quad r \ge 0 \quad \mathrm{et} \quad θ > 0 \; ;\]
- il reste à ajuster le paramètre θ de la loi de Rayleigh aux données et à vérifier l'adéquation du modèle ajusté aux données.
Vous disposez de trois jeux de données obtenus sur le chromosome 4 (humain) et la figure ci-dessous, dans sa partie haute, vous permettra de visualiser les positions relatives des marqueurs5 :
- le fichier http://xtof.disque.math.cnrs.fr/data/CoursStat2013short.txt contient 96 mesures avec les marqueurs placés aux positions
C4-71etC4-15; c'est-à-dire avec une distance linéaire de 10 Mbp ; - le fichier http://xtof.disque.math.cnrs.fr/data/CoursStat2013medium.txt contient 249 mesures avec les marqueurs placés aux positions
E4etC4-46; c'est-à-dire avec une distance linéaire de 64 Mbp ; - le fichier http://xtof.disque.math.cnrs.fr/data/CoursStat2013long.txt contient 132 mesures avec les marqueurs placés aux positions
E4etC4-161; c'est-à-dire avec une distance linéaire de 192 Mbp.
Vous pourrez charger ces données dans votre espace de travail avec, par exemple :
court <- scan("http://xtof.disque.math.cnrs.fr/data/CoursStat2013short.txt") moyen <- scan("http://xtof.disque.math.cnrs.fr/data/CoursStat2013medium.txt") long <- scan("http://xtof.disque.math.cnrs.fr/data/CoursStat2013long.txt")
Chaque fichier contient les distances mesurées en μm.
- Question 2.1 : vous écrirez la log-vraisemblance, la fonction score et l'information observée pour un échantillon de taille N, IID, suivant une loi de Rayleigh. Vous en déduirez l'expression analytique de l'estimateur du maximum de vraisemblance ;
- Question 2.2 : pour chacun des trois jeux de données vous trouverez l'estimateur du maximum de vraisemblance du paramètre θ de la loi de Rayleigh ainsi qu'un intervalle de confiance à 95% avec la méthode de Wald ;
- Question 2.3 : pour chacun des trois jeux de données vous construirez le graphe de la fonction de log-vraisemblance au voisinage de son maximum (sur un domaine long, par exemple, de six fois l'erreur type) auquel vous superposerez l'approximation quadratique : \[y = l(\hat{θ}) - (\hat{θ} - θ)^2 / (2 \hat{σ}_{\hat{θ}}^2)\; ; \]
- Question 2.4 : pour chacun des trois jeux de données vous construirez un histogramme des observations auquel vous superposerez la loi de Rayleigh ajustée, ou mieux, vous construirez un hanging rootogram (je vous conseille d'utiliser 20 bins pour vos histogrammes ou hanging rootograms). Le modèle ajusté vous semble-t-il satisfaisant ?
- Question 2.5 : vous construirez un graphe représentant votre paramètre estimé \(\hat{θ}\) en fonction de la racine carrée de la distance linéaire séparant les marqueurs. Qu'en concluez-vous sachant que l'écart type de la distance euclidienne entre l'origine et la fin d'une marche aléatoire croît comme la racine du nombre de pas quelle comporte ?
- Question 2.6 : pour un des jeux de données, vous étudierez la probabilité de recouvrement d'un intervalle de confiance à 95% obtenu avec la méthode de Wald par bootstrap paramétrique (comme nous l'avons fait dans la section 3.6.3 du cours). Pour cela, vous trouverez la fonction de répartition en intégrant la densité, vous trouverez l'inverse de cette fonction de répartition et vous utiliserez la méthode de la transformée inverse (section 3.8.2 du cours) pour simuler vos échantillons.
5.4 Réponses
5.4.1 Question 2.1
Soient \(R_1,\ldots,R_N\) N variables aléatoires IID suivant une loi de Rayleigh de paramètre θ. La densité de probabilité conjointe s'écrit : \[p(R_1=r_1,\ldots,R_N=r_n) = \prod_{i=1}^N \frac{r_i}{θ^2} \, \exp\left(\frac{-r_i^2}{2\, θ^2}\right) \; .\] La log-vraisemblance s'écrit donc : \[\mathcal{l}(θ) = -2 N \log θ - \frac{1}{2\, θ^2} \sum_{i=1}^N r_i^2 \, ,\] où le terme \(\sum_{i=1}^N \log r_i\) a été éliminé puisqu'il ne dépend pas de θ. La fonction score est donc : \[S(θ) = -\frac{2 N}{θ} + \frac{1}{θ^3} \sum_{i=1}^N r_i^2 \] et l'information observée : \[\mathcal{J}(θ) = -\frac{2 N}{θ^2} + \frac{3}{θ^4} \sum_{i=1}^N r_i^2 \; .\] L'estimateur du maximum de vraisemblance (EMV), dans les bons cas au moins, est la (ou une des) racine(s) de la fonction score, ce qui nous donne ici : \[\hat{θ} = \sqrt{\frac{\sum_{i=1}^N r_i^2}{2 N}} \; .\] On voit de plus que : \[\mathcal{J}(\hat{θ}) = \frac{8 N^2}{\sum_{i=1}^N r_i^2} > 0\] on a donc bien un maximum puisque l'information observée est l'opposée de la dérivée seconde.
5.4.2 Question 2.2
Il suffit d'écrire une fonction qui renvoie par exemple l'EMV, l'erreur type (racine carrée de l'inverse de l'information observée évaluée à l'EMV) et les bornes gauches et droites de l'intervalle de confiance :
toutEnUn <- function(distances) { N <- length(distances) r2 <- sum(distances^2) theta.chapeau <- sqrt(r2/2/N) sigma.chapeau <- sqrt(r2/2)/2/N gauche <- theta.chapeau - 1.96*sigma.chapeau droite <- theta.chapeau + 1.96*sigma.chapeau c(emv=theta.chapeau, erreurType=sigma.chapeau, icGauche=gauche, icDroite=droite)}
Nous obtenons donc pour les trois jeux de données :
court.res <- toutEnUn(court) moyen.res <- toutEnUn(moyen) long.res <- toutEnUn(long) cbind(court.res, moyen.res, long.res)
| 1.12377757659898 | 2.08121325057705 | 3.31684629100925 |
| 0.0573475343135193 | 0.0659457653701778 | 0.14434720687606 |
| 1.01137640934448 | 1.95195955045151 | 3.03392576553217 |
| 1.23617874385347 | 2.2104669507026 | 3.59976681648633 |
5.4.3 Question 2.3
Le plus simple est de définir une fonction qui génère un graphe comme demandé pour un jeu de données passé comme paramètre :
grapheApproxQuad <- function(distances) { stats <- toutEnUn(distances) N <- length(distances) r2 <- sum(distances^2) ll <- function(theta) -2*N*log(theta) - r2/2/theta^2 tt <- (-200:200)/200*stats[2]*6+stats[1] plot(tt,ll(tt),type="l", xlab="theta",ylab="log-vraisemblance") lines(tt,ll(stats[1])-(tt-stats[1])^2/2/stats[2]^2, col=2,lty=2) }
Et on obtient les figures avec :
layout(matrix(1:3,nc=3))
par(cex=2)
grapheApproxQuad(court)
grapheApproxQuad(moyen)
grapheApproxQuad(long)
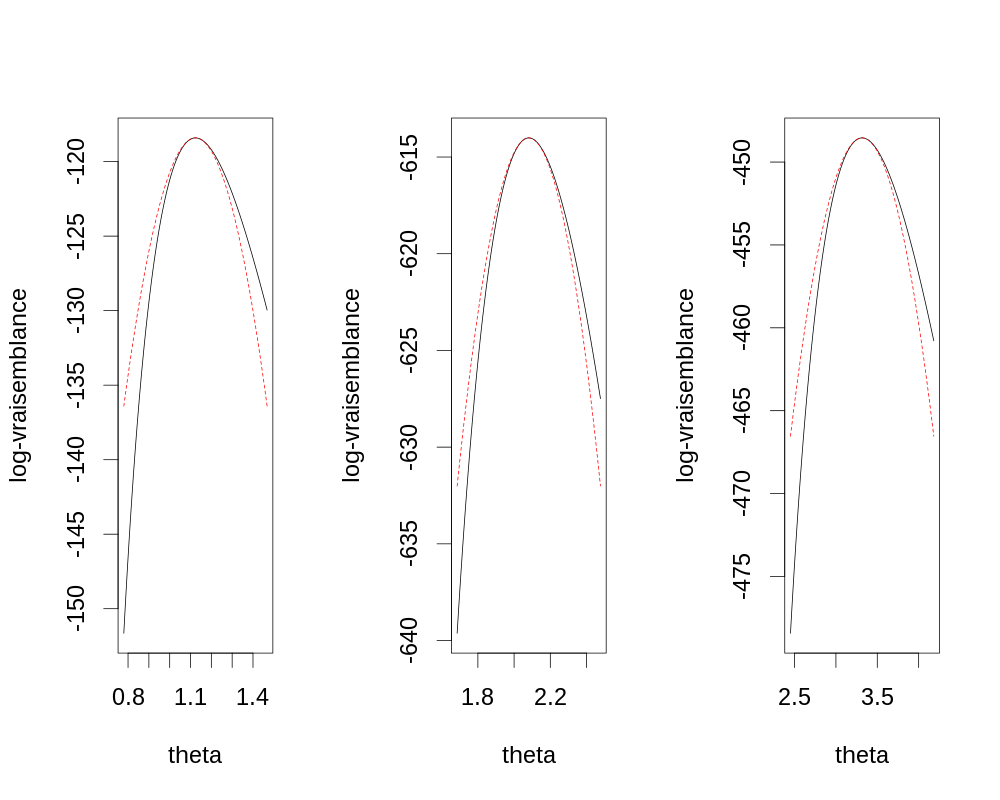
Figure 28 : Log-vraisemblance et approximation quadratique pour les trois jeux de données : court (gauche), moyen (milieu) et long (droite).
On constate que nos fonctions de log-vraisemblance sont légèrement asymétriques et on s'attend donc à ce que nos intervalles basés sur la méthode de Wald soient légèrement faux.
5.4.4 Question 2.4
Je vais faire les hanging rootograms en passant, encore une fois, par la définition d'une fonction. Pour faire les choses proprement, j'ai besoin de l'expression de la fonction de répartition d'une loi de Rayleigh : \[F(r|θ) = \int_0^r f(u|θ) du = \int_0^r \frac{u}{θ^2} \exp \left(\frac{-u^2}{2θ^2}\right) du = \int_0^r d\left[-\exp \left(\frac{-u^2}{2θ^2}\right)\right] = 1 - \exp \left(\frac{-r^2}{2θ^2}\right) \; .\]
D'où :
hangingRooto <- function(distances, br=20) { stats <- toutEnUn(distances) N <- length(distances) F <- function(r) 1-exp(-r^2/2/stats[1]^2) dist.hist <- hist(distances,breaks=br,plot=FALSE) Y <- dist.hist$counts X <- dist.hist$mids pred <- diff(F(dist.hist$breaks)*N) plot(X,sqrt(Y)-sqrt(pred),type="l", xlab="Distance (μm)",ylab="") abline(h=1.96/2,col=2,lty=2) abline(h=-1.96/2,col=2,lty=2) }
Et on construit les trois figures :
layout(matrix(1:3,nc=3))
par(cex=2)
hangingRooto(court)
hangingRooto(moyen)
hangingRooto(long)
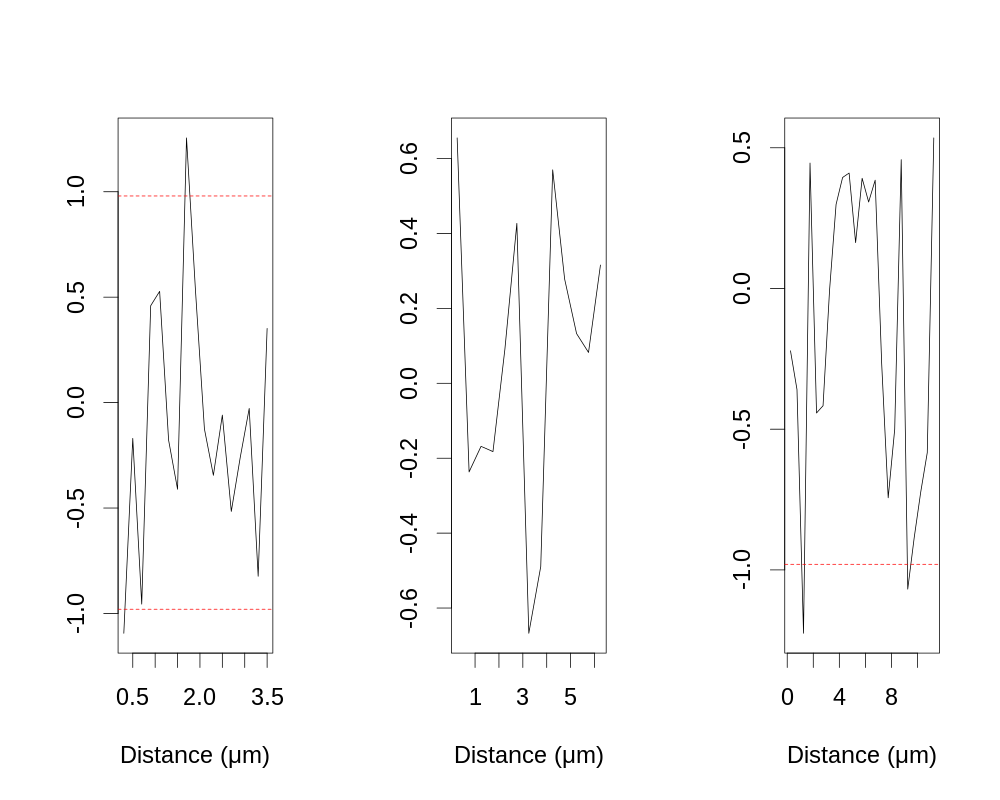
Figure 29 : Hanging rootograms des trois jeux de données (court à gauche, moyen au milieu et long à droite) ajustés par une loi de Rayleigh. Les intervalles de confiances à 95% sont figurés par les lignes pointillées rouges.
Les ajustements sont plutôt bons !
5.4.5 Question 2.5
par(cex=2) plot(sqrt(c(10,64,192)), c(court.res[1], moyen.res[1], long.res[1]), xlab="Racine carrée de la séparation entre marqueurs (Mbp)", ylab="Paramètre de la loi de Rayleigh (μm)") lines(sqrt(c(10,192)), c(court.res[1], long.res[1]), col=2,lty=2)
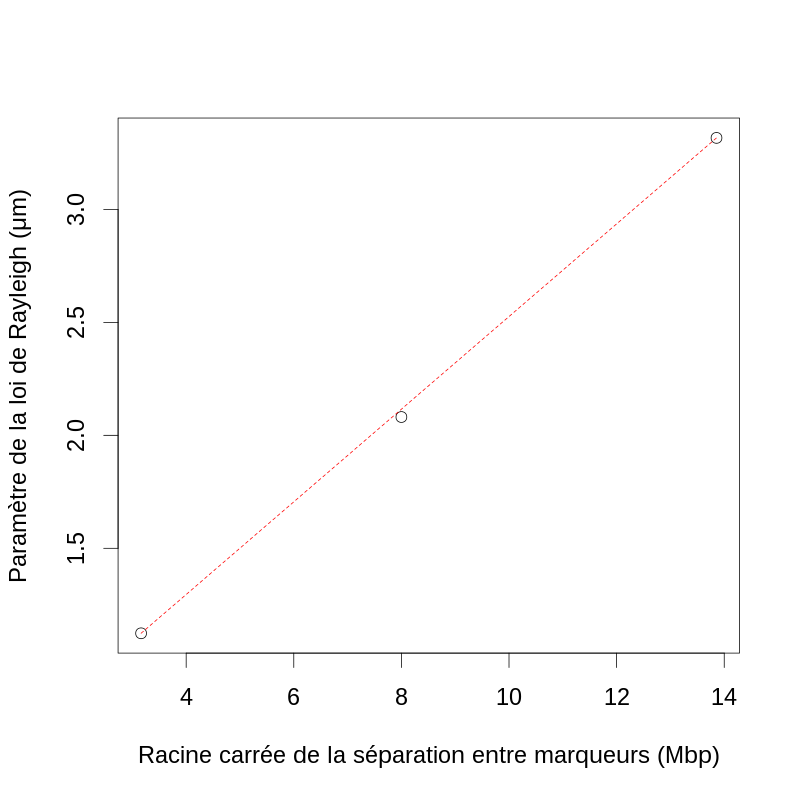
Figure 30 : Paramètre estimé de la loi de Rayleigh en fonction de la racine carrée de la séparation entre marqueurs (en Mbp).
Le modèle est satisfaisant jusque là !
5.4.6 Question 2.6
L'expression de la fonction de répartition établie dans la question précédente nous donne rapidement l'expression de la fonction inverse : \[F^{-1}(u) = θ \sqrt{- 2 \log u} \; ,\]
d'où la réponse à la question en définissant d'abord une fonction générale :
paraBoot <- function(distances, nrep=10000) { stats <- toutEnUn(distances) N <- length(distances) theta <- stats[1] boot.rep <- sapply(1:nrep, function(i) { dist.boot <- theta*sqrt(-2*log(runif(N))) stats.boot <- toutEnUn(dist.boot) stats.boot[3] <= theta & theta <= stats.boot[4]}) c(sum(boot.rep),nrep,sum(boot.rep)/nrep)}
On peut alors obtenir les probabilités de recouvrement pour les trois cas avec :
set.seed(20100928)
cbind(paraBoot(court),
paraBoot(moyen),
paraBoot(long))
| 9463 | 9490 | 9473 |
| 10000 | 10000 | 10000 |
| 0.9463 | 0.949 | 0.9473 |
On voit que les probabilités de recouvrement empiriques sont très proches des probabilités nominales (0,95), malgré la légère asymétrie de la fonction de log-vraisemblance que nous avions constaté précédemment.
Notes de bas de page:
Nous préférerons la valeur « exacte » plutôt que l'approximation \(\int_{g_i}^{d_i} χ^2_1(x) \, dx \approx (d_i-g_i) \, χ^2_1\left((d_i-g_i)/2\right)\) car la première est directement disponible dans R est qu'elle est bien plus précise étant données les bins que nous avons choisis.
Comme je vous l'avais dit en cours, vous n'étiez pas forcés de procéder comme moi en deux temps ; c'est-à-dire que vous pouviez définir votre équivalent de FLVvraie comme une fonction du paramètre θ et des données.
Prenez une loi gaussienne istrope à 2D et passez en coordonnées polaires : http://fr.wikipedia.org/wiki/Loi_de_Rayleigh.
Figure 1 de Yokota et col. (1995) Evidence for the organization of chromatin in megabase pair-sized loops arranged along a random walk path in the human G0/G1 interphase nucleus. The Journal of Cell Biology 130(6), 1239-1249.